Python 활성화함수

Jayce_97·2023년 6월 19일

python 활성화함수

활성화함수(Activation Function)

종류

Python 인공신경망

목록 보기

3/3

이번 시간은 인공지능신경망을 배울 때 나온 활성화 함수에 대해 자세히 배워보도록 하겠습니다.

활성화함수(Activation Function)

활성화 함수이란 인공 신경망(Neural Network)에서 사용되는 은닉층(Hidden Layer)을 활성화 하기 위한 함수입니다.
순전파와 역전파의 풀이처럼 가중치와 편향을 갱신하기 위해 사용됩니다.
인공신경망에서 활성화 함수는 입력 데이터를 다음 레이어 출력 방식을 결정하는 역할로써 매우 중요합니다.
즉, 활성화 함수는 입력을 받아서 활성화 또는 비활성화를 결정하는 함수입니다.

순전파 : 입력층에서 은닉층 방향으로 이동하면서 각 입력에 해당하는 가중치가 곱해지고, 결과적으로 가중치 합으로 계산되어 은닉층 뉴런의 함수 값(일반적으로 시그모이드(Sigmoid) 사용)이 입력됩니다. 그리고 최종 결과가 출력됩니다.
역전파 : 역전파 알고리즘은 input과 output 값을 알고 있는 상태에서 신경망을 학습 시키는 방법입니다. 이 방법을 Supervised learning(지도학습)이라고 합니다. 초기 가중치, weight 값은 랜덤으로 주어지고 각각 노드들은 하나의 퍼셉트론으로, 노드를 지날때 마다 활성함수를 적용합니다.

종류

Sigmoid 함수
시그모이드 함수는 로지스틱 함수라고 불리며, X의 값에 의해 0~1의 값을 S자형으로 출력하는 함수입니다.

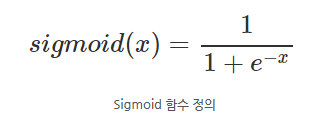
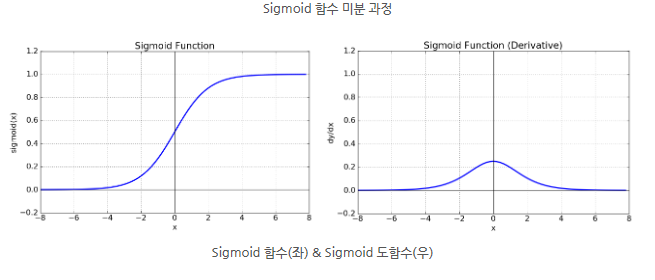
시그모이드 함수는 음수 값을 0에 가깝게 표현하기 때문에 영향력이 적어지는 현상이 발 생할 수있습니다. 즉, 미분함수에 대해 일정 값 이상의 미분값이 소실되는 현상이 있습니다.
함수의 중심이 0이 아니기 때문에 학습이 느려지는 단점이 있습니다.

Tanh 함수
탄함수는 쌍곡선 함수 중 하나로 시그모이드 함수의 변형 형태입니다.

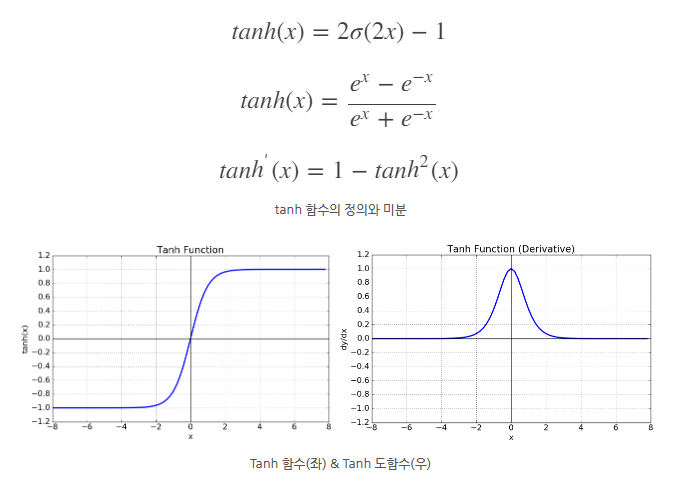
함수의 중심점을 0으로 옮겨 시그모이드의 단점을 해결했으나, 미분함수에 대해 일정 값 이상의 미분값이 소실되는 현상이 있습니다.
ReLU(경사) 함수
렐루 함수는 가장 많이 사용되는 함수 중 하나이며, 시그모이드와 탄의 값의 손실되는 현상을 해결 할 수 있습니다.

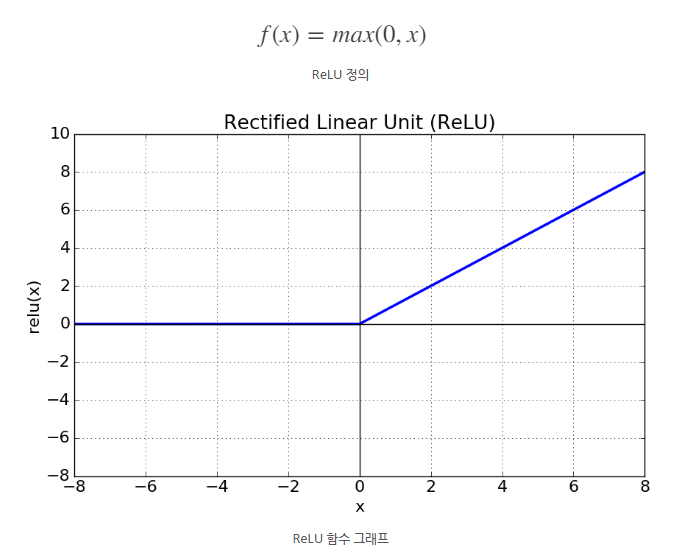
X가 0보다 크면 기울기가 1인 직선이 되고, 0보다 작으면 함수 값이 0 이 됩니다.
그로인해 0보다 작은 값들은 뉴런이 없어 질 수 있다는 단점이 발생할 수 있습니다.
학습이 빠르고, 연산비용이 작다는 장점과 구현이 매우 간단하는 특징을 가지고 있습니다.
이외의 방식으로는 렐루 함수의 단점을 보안한 Leaky ReLU, PReLU등 여러가지 방법이 더 존재합니다.
Softmax 함수
소프트 맥수 함수는 입력받은 값을 0~1 사이로 모두 정규화합니다.
출력 값들의 총합은 항상 1이 되는 특성을 가지고 있습니다.

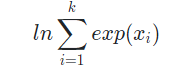
값 만들기

input

import numpy as np 
import matplotlib.pyplot as plt 

def step_function(x):
    return np.array(x>0, dtype=np.int64) # 0보다 크면 1, 작으면 0 

X=np.arange(-5, 5, 0.1)    
y=step_function(X)
plt.plot(X,y)
plt.ylim(-0.1, 1.1)
plt.show()

output

Sigmoid 함수 만들기

input

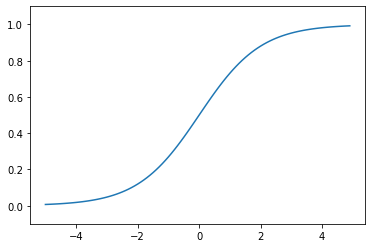
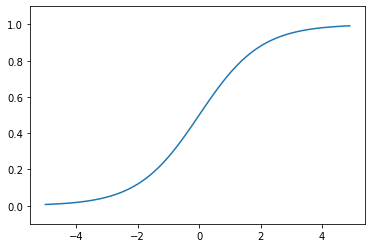
def sigmoid(x):
    return 1/(1+np.exp(-x)) # 0.0~1.0으로 출력됨 

X=np.arange(-5, 5, 0.1)    
y=sigmoid(X)
print(y) 
plt.plot(X,y)
plt.ylim(-0.1, 1.1)
plt.show()

output

0~1 사이의 값을 이용한 시그모이드 함수입니다.

Tanh 함수만들기

input

X=np.linspace(-np.pi, np.pi, 12)
y=np.tanh(X)
print(X)
print(y)
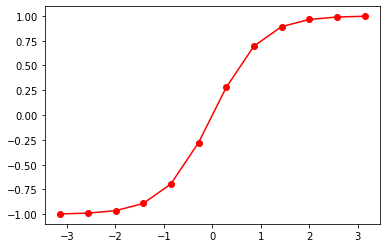
plt.plot(X,y,c='r',marker='o')
plt.show()
# 출력값의 범위 -1 ~ 1

output

-1 ~ 1인 탄 함수입니다.

ReLU 함수만들기

input

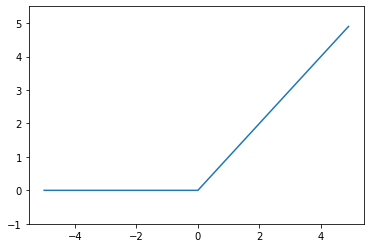
def relu(x):
    return np.maximum(0,x)

x=np.arange(-5, 5, 0.1)    
y=relu(x)
plt.plot(x,y)
plt.ylim(-1, 5.5)
plt.show()
# x>0 => 그대로 출력, x<=0 => 0

output

0이 하의 값은 0으로 만들어주는 렐루 함수입니다.

Softmax 함수 만들기

input

def softmax(a):
    c=np.max(a) #입력값의 최대값
    exp_a=np.exp(a-c) #무한대 문제를 해결하기 위하여 최대값을 차감
    sum_exp_a=np.sum(exp_a)
    y=exp_a / sum_exp_a 
    return y 

a=np.array([0.3, 2.9, 4])
print(softmax(a))
a=np.array([1000, 1100, 1200])
print(softmax(a))
print(np.sum(softmax(a))) #소프트맥스 함수의 총합은 1