[Crash Course: Computer Science] #3 부울 연산과 논리 게이트: 컴퓨터 과학 특강

지난 강의에서 우리는 컴퓨터가 어떻게 전자 기계 장치로 진화해 왔는지를 살펴봤다.
기어의 톱니바퀴로 10진수를 표현했던 기계부터, 트랜지스터가 전류의 흐름으로 켜고 끌 수 있는 전자식 컴퓨터가 되기까지!

이번 시간에는 원시적인 전기 신호부터 부울 연산을 배운다.

이진(Binary): 2가지의 전기적 상태만으로 우리는 중요한 정보를 표현할 수 있다.
이 2가지 상태는 정확히 "참"과 "거짓"으로 나타내는 데 필요하다. 우리는 true와 false를 이진수인 1과 0을 사용해 나타낼 수 있다.

-On상태 : 컴퓨터 안에서 전류가 흐르고 true를 나타내는 상태.
-Off상태 : 컴퓨터 안에서 전류가 흐르지 않고 false를 나타내는 상태.

<이진법을 사용하는 이유>
1. 어떤 초기의 전자 컴퓨터는 3개의 상태를 갖고 있는 3진법(ternary)을 사용하거나 5진법(quinary)을 사용하기도 했음.

하지만 on과 off 2개만 사용할 때 신호가 가장 명확하다.
중간 상태가 존재할 경우 상태를 나누기가 어려움. ex. 스마트폰 배터리가 부족할 때 누가 옆에서 전자레인지를 사용하면 전기적인 잡음이 생겨 신호가 섞일 수 있다.

2. 수학 분야에 이미 Boolean Algebra가 있어서 참과 거짓을 조작하는 데 필요한 규칙과 연산 방법을 모두 알아냄. Boolean Algebra는 영국의 수학자 George Boole이라는 사람의 이름을 따서 만들었는데 그는 under, over, beyond의 상태를 나타내는 논리적 표현에 관심이 있었다. 부울의 접근은 1847년에 낸 "The mathematical analysis of logic"이라는 첫번째 저서에서 논리 방정식을 통해 공식적이고 체계적으로 증명이 되었다.

Boolean Alegebra에는 NOT,AND,OR라는 핵심적 연산이 있다.
-Not : 하나의 Boolean 값을 취하고 참은 거짓으로, 거짓은 참으로 뒤집는다.

Input이 true일 경우 Output은 false
input이 false일 경우 output은 true

트랜지스터는 단순히 전기 조절 스위치가 아니다. 제어선과 두개의 전극을 가지고 있다. 제어선에 전기를 제공하면 하나의 전극에 전류를 흐를 수 있게 하고, 트랜지스터를 통해 다른 전극에도 전류가 흐를 수 있게 된다.

트랜지스터에 있는 부울 논리도 배울 수 있다.
제어선이 input이고 전극을 output으로 생각할 수도 있으며, 하나의 트랜지스터로 하나의 입력과 하나의 출력이 가능해지는 것. 입력을 켜면 출력이 켜지고 전류가 지나갈 수 있으므로 입력이 참이면 출력도 참! 입력을 끄면 출력이 꺼지고 전류도 지나갈 수 없으므로 입력이 거짓이면 출력도 거짓!

회로가 Not을 만들도록 수정한다면? input과 output이 달라진다. 트랜지스터의 끝 부분에 있는 출력선(output wire)을 앞으로 조금 움직여보자. 입력을 켜면 트랜지스터가 전류를 통과시켜 접지 상태가 되고, 입력은 켜지고 출력은 꺼진 상태가 된다(input on, output off). 반대로 트랜지스터를 끄면, 전류는 접지 상태가 되는 바닥으로 흐르지 못하게 되고 대신 전류는 출력선(output wire)를 통해 흐른다(input off, output on). 이것은 NOT게이트라 부른다. 게이트가 전류의 흐름을 통제하기 때문이다. 두 개의 입력, 한 개의 출력. 모든 입력인 참일 경우에만 출력이 참. ex. 내 이름은 캐리 앤(참), 파란 드레스를 입고 있지(참). =>(참) 내 이름은 캐리 앤(참), 바지를 입고 있지(거짓). => (거짓) 나는 바지를 입고 있고, 내 이름은 캐리 앤이다. => (거짓) 내 이름은 캐리앤이 아니고, 나는 바지를 입고 있다. => (거짓) And Gate를 떠올려 보자. 트랜지스터 A와 B가 있다. 둘 중 하나만 켜져있으면 출력선에 전류가 흐를 수 없고, 둘 다 켜져 있어야 출력선에 전류가 흐를 수 있다. 하나의 입력만 참이어도 출력이 참이된다. ex. 내 이름은 마가렛이거나 파란드레스를 입고 있다.라는 문장에서 둘 중 하나만 충족하거나 둘 다 충족할 경우 참인 문장이 된다. 둘 다 틀려야만 거짓!

Or Gate를 떠올려 보자.
트랜지스터를 직렬로 놓는 대신 병렬로 놓고 전류원과 연결.
만약 두개의 트랜지스터가 꺼져 있다면 ? 전류는 출력으로 흐르지 않음.
하지만 둘 중 하나만 켜져있어도 전류는 출력이 켜진다.

<게이트를 기준으로 칭하는 기호>

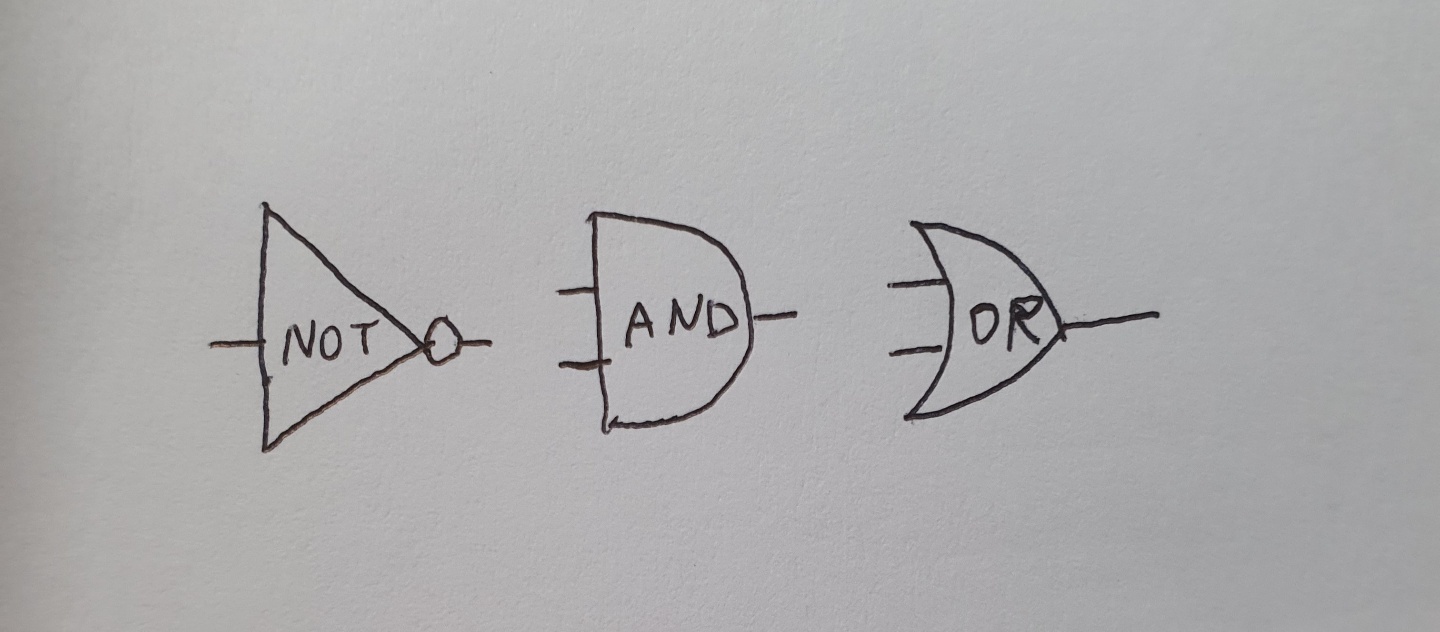
NOT : 삼각형과 점
AND : D 모양
OR : 우주선 모양

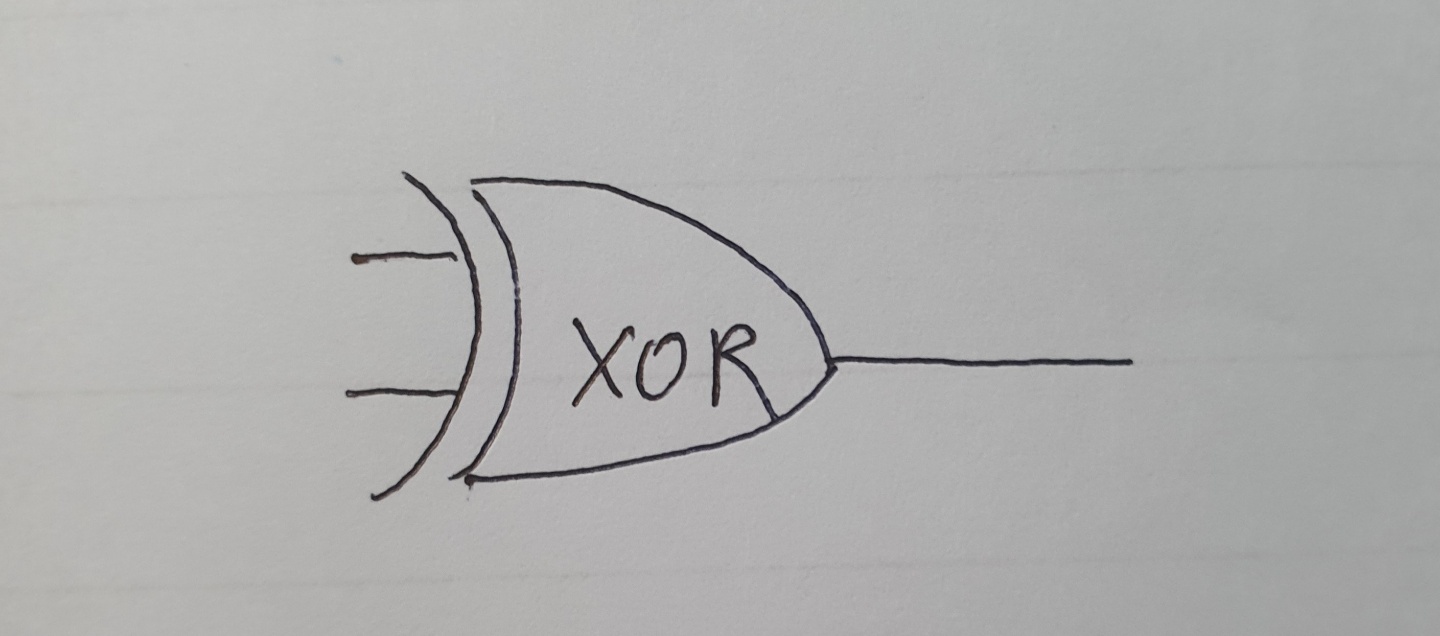
보통의 OR 연산자와 같지만 중요한 차이가 있다.
모든 입력이 참이면, XOR의 출력은 거짓!!

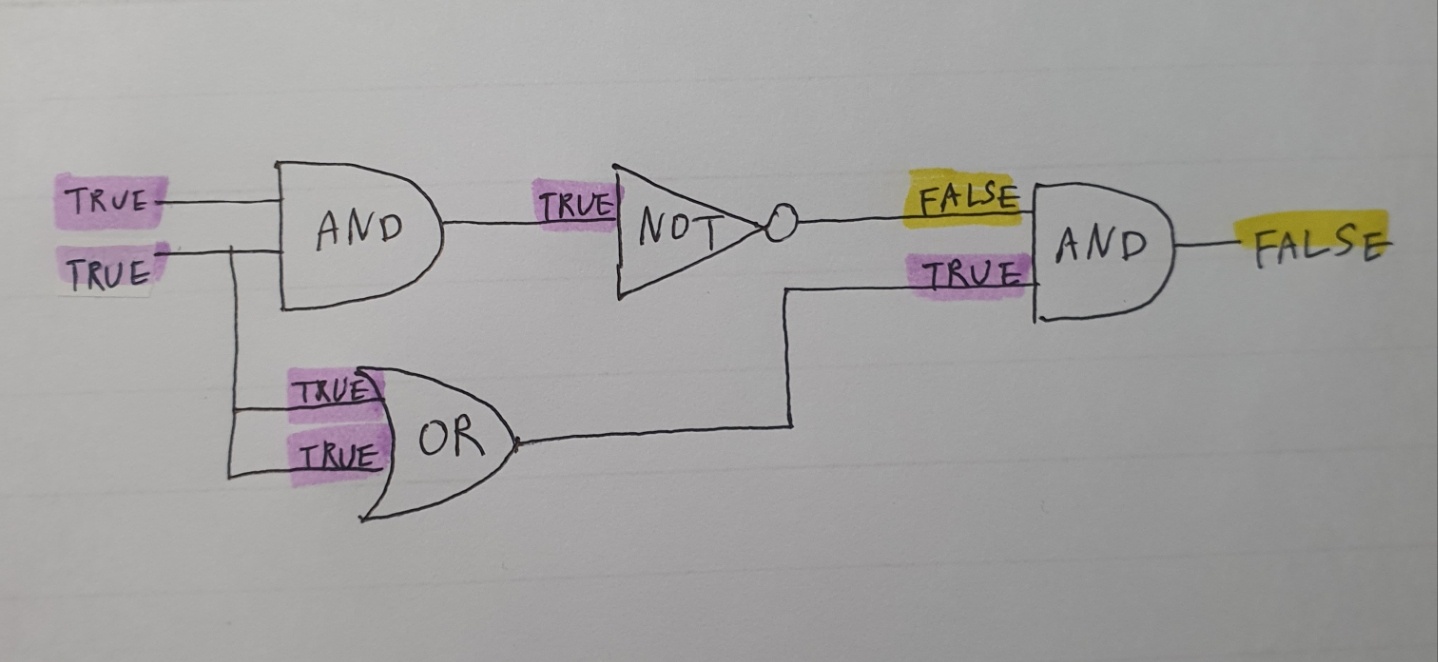
OR 게이트에 AND게이트를 추가해보자.
AND게이트에서 입력이 둘 다 True일 때 출력은 True가 된다. 이 때 바로 뒤에 NOT게이트를 추가하면 True를 False로 뒤집는다.
최종적으로 AND 게이트를 하나 더 놓고, OR 게이트의 출력을 함께 내보낸다고 해보자.
이 때 최종 AND는 OR게이트가 True일 때 False가 된다.

이 강의에서 배운 논리 회로만으로 우리는 복잡한 논리문을 평가하는 시스템을 만들 수 있다.