문제

이 문제는 아주 평범한 배낭에 관한 문제이다.

한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.

준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.

입력

첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.

입력으로 주어지는 모든 수는 정수이다.

출력

한 줄에 배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 출력한다.

예제 입력 1

4 7
6 13
4 8
3 6
5 12

예제 출력 1

14

안 풀려서 답을 찾아봤는데 잘 찾아봤다고 생각이 드는 문제였다.
https://gsmesie692.tistory.com/113
이 분 게시물을 읽고 이해했습니다.. 감사합니다..~~

이 문제가 해결하려고 하는 수식은 이렇다.
출처: https://en.wikipedia.org/wiki/Knapsack_problem

maximize $\sum _{i=1}^{n}v_{i}x_{i}$
subject to $\sum _{i=1}^{n}w_{i}x_{i}\leq W$ and $x_{i}\in \{0,1\}$

x는 0 또는 1의 값만 가질 수 있다. (그래서 0-1 knapsack인 것)
각각의 value에 0또는 1을 곱한 값의 내적을 극대화하되, 배낭에 넣을 수 있는 물건의 무게 제한이 W만큼 있는 것이다.

knapsack problem에는

• 분할 가능한(fractional) 배낭문제
• 0-1 배낭 문제

이렇게 있다고 한다. 이번에 풀어본 문제가 0-1 배낭문제이고, 분할 가능한 배낭문제는 아직 안풀어봤지만 그리디로 접근하는 문제라고 한다. 다음에 풀어봐야지!!

여튼 0-1 배낭 문제는 DP로 접근하거나 백트래킹으로도 구현할 수 있다고 한다. 이번 시간에는 DP로 접근을 해보았다.

2차원 표를 그려 접근한다.
열(w): 문제의 예시에서 가방의 최대 무게 한도는 7이지만, 무게 한도가 0일 때부터 1씩 늘려나갈 때 얻을 수 있는 최대 value를 채워넣는 것이다.
행(i): 특정 물건(i)이 특정 무게(w)에서 포함될지 말지를 결정한다.

물건 i를 하나씩 순회하면서 (한 행씩 내려오면서) 가방의 최대 무게 한도가 w일 때는 이 짐을 넣는 것이 최선인가?를 고민해서 yes이면 포함시키고, no이면 포함시키지 않는 것이다.

접근 과정

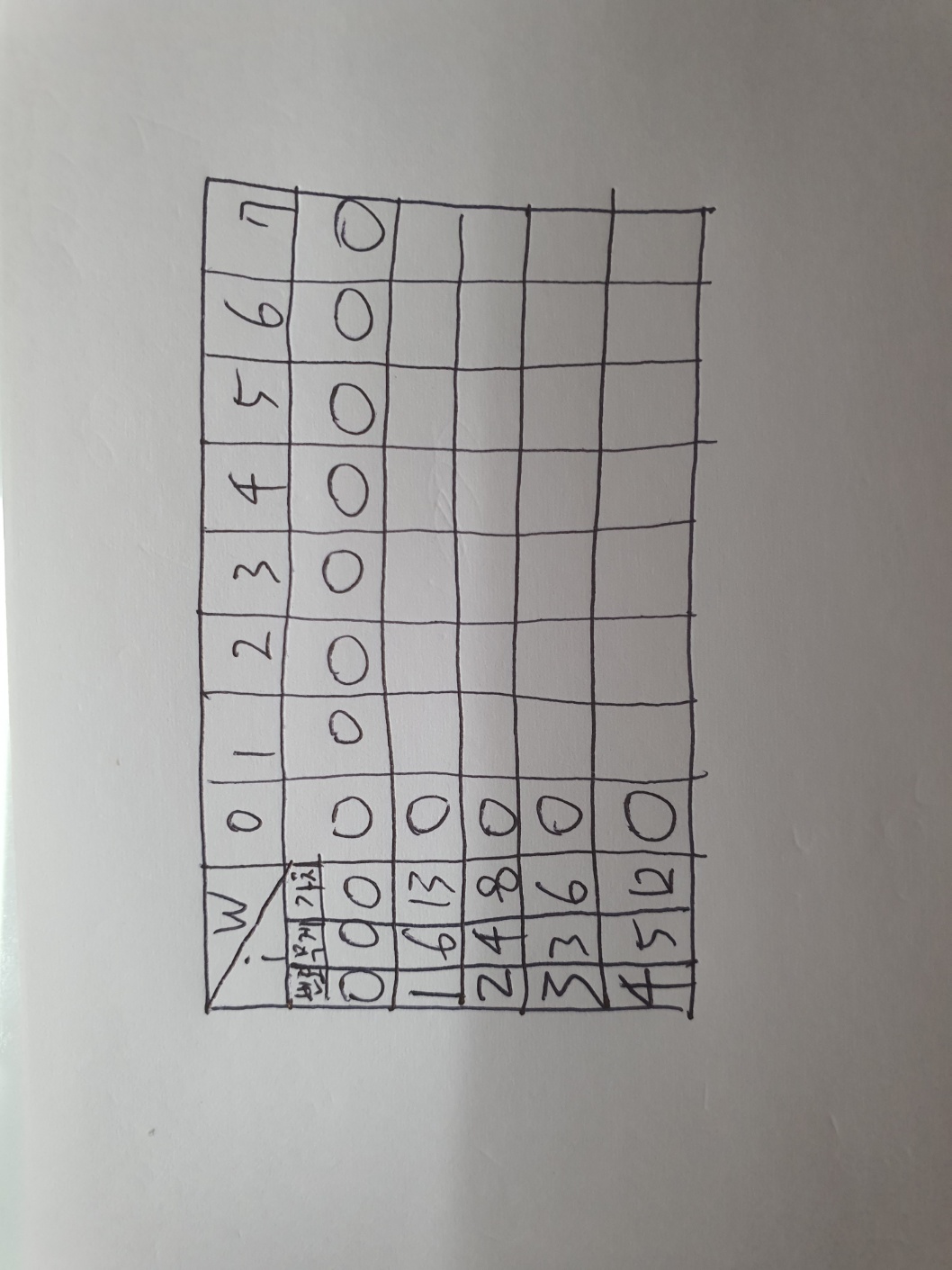
0행과 0열을 모두 0으로 채워넣는다.
넣을 짐도 없고 가방의 최대 무게 한도도 0이라면 얻을 수 있는 최대 value도 0이다.

다음으로는 i가 1일 때이다. (첫번째 물건)
물건1의 무게는 6이고 value는 13이군.
이때 가방의 최대 한도가 1일 때부터 시작해서 문제에서 주어진 7일때까지 1씩 늘려나가며 칸을 채워보자.
우선 가방 무게 최대 한도가 6 미만이라면?
물건1의 무게가 6인데 그것보다도 한도가 작으면 아무 물건도 못 넣는다.
그래서 얻을 수 있는 value도 없고 모조리 0으로 채운다. (헷갈려서 다시 언급하지만 value를 넣는 것이다.) i가 1인데 w < 6이면 dp[i][w] = 0인 것이다.
그런데 만약 가방 무게 최대 한도가 6이라면? 드디어 물건1을 넣을 수 있게 되고, 이때 얻는 최대 value는 13이다. 근데 이건 가방 무게 최대 한도가 7일 때도 마찬가지이다. 그래서 dp[1][6]과 dp[1][7]에는 13을 채워넣는다.

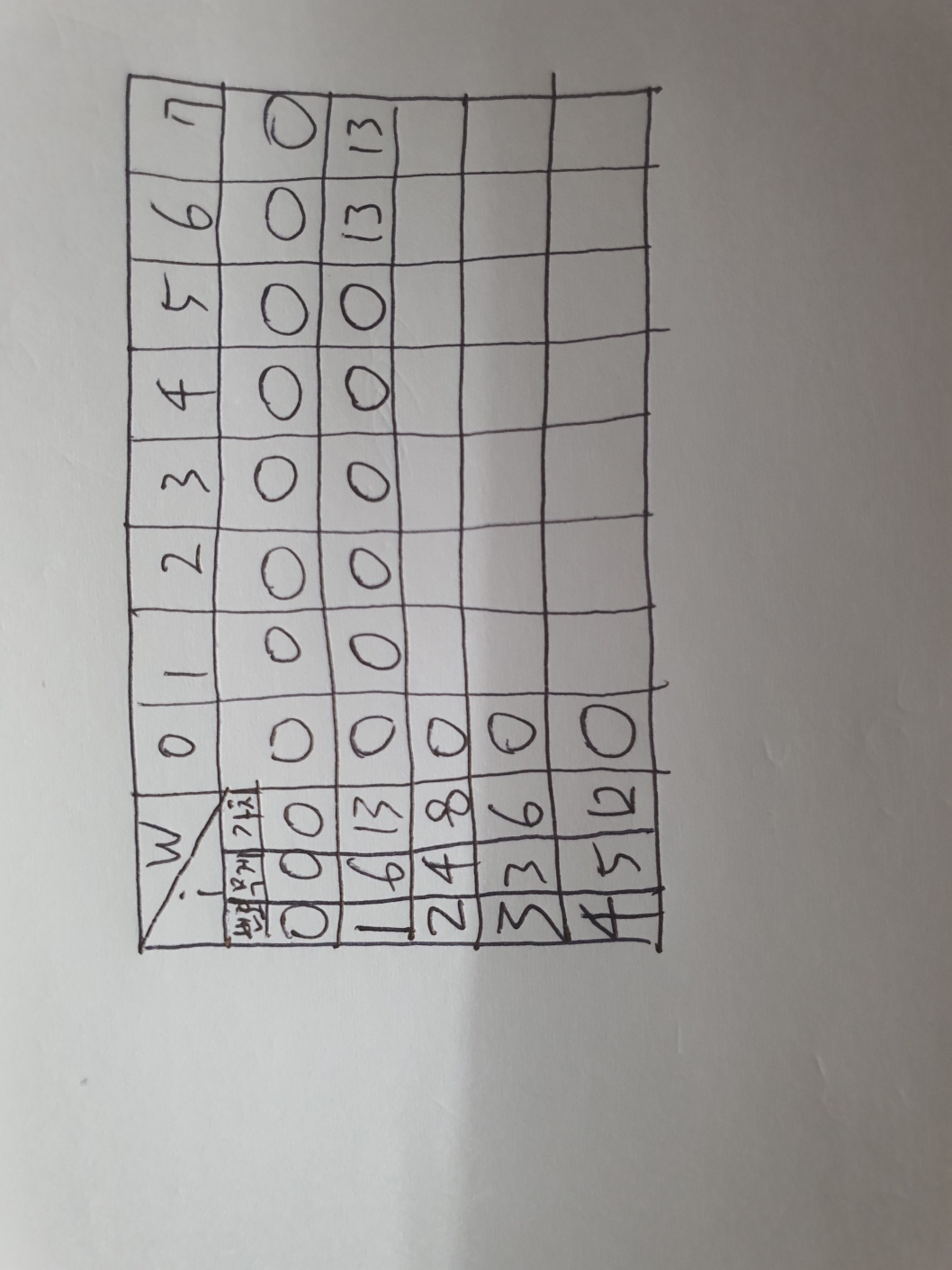
다음으로는 i가 2일 때이다. (2번째 물건)
물건 2의 무게는 4이고, value는 8이다.
이 때 가방 최대 무게가 4 미만이면 물건 1도 못넣고 물건 2도 못넣으므로 모조리 0으로 채운다.

그런데 만약 최대 무게가 4라면? 이때는 물건2를 넣을 수 있는 상태이고 넣을지 말지 결정을 해야 한다.

• 만약 물건2를 넣게 되면 최대 value는 8이다.
• 만약 물건2를 포기하면 최대 value는 0이다.

그럼 넣는게 이득이네? i가 2이고 w가 4일 때는 칸에 8을 채워준다.
최대 무게가 5일 때도 마찬가지이다.
가방의 최대 무게가 5일 때는 물건 1은 못넣지만 물건 2는 넣을 수 있으니까 최대 value는 8이다!

그런데 최대 무게가 6이라면?
이때 접근법을 잘 이해해야 0-1 knapsack문제의 원리를 이해할 수 있는 것이었다.
i가 2이고 현재 가방 최대 무게가 6이라고 가정하면 고려할 수 있는 2가지 선택지가 있다.

• ✅ 그냥 2번째 물건을 안 넣음 ㅅㄱ -> 무게가 6일 때 1번째 물건을 넣었을 때 최대 value가 13이었으므로 그대로 가져와서 13으로 채운다.
• [여기서는 선택 불가] 다시 1번 배낭을 고려하는 셈 치고 최대 무게는 그대로 6일 때, 무게에서 2번 가방의 무게인 8만큼을 비워준다. -> 6 - 8 < 0이므로 물건 1과 물건 2를 같이 넣기에는 비워줄 자리가 충분치 않다.

따라서 여기는 13을 채운다.
최대 무게가 7일 때도 같은 이유로 13을 채운다.

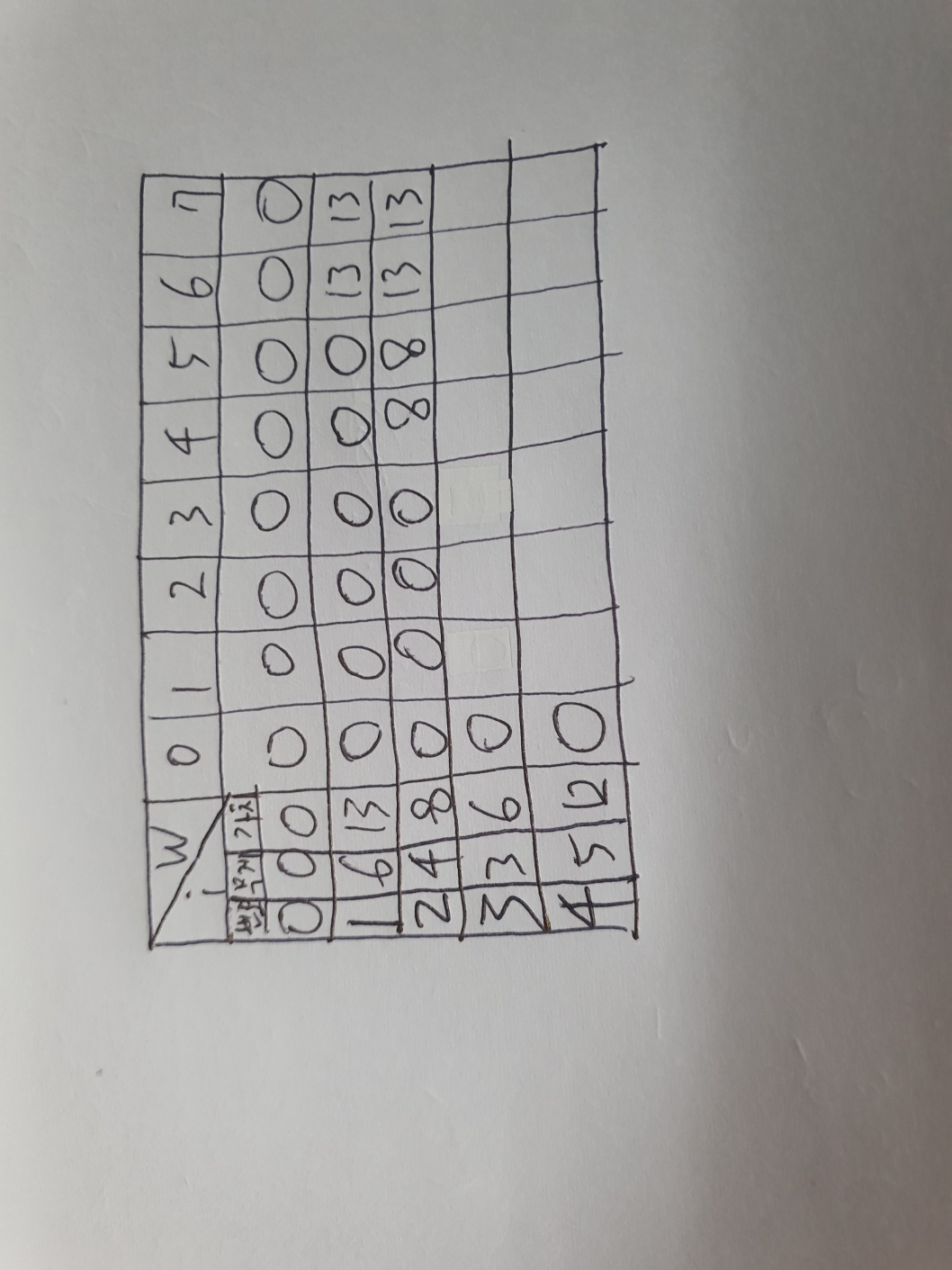
다음으로는 i가 3일 때다.

마찬가지로 w가 3번물건의 무게인 3보다 작을 때는 0으로 채워넣는다.

w가 3이라면? 물건 3을 넣을 수 있다. 넣고 value 6으로 채운다.

재미있는 건 w가 7일 때이다.

w가 7이라고 계속 가정을 하고 다시 i-1인 물건 2를 고려할 때로 돌아가본다면? 물건 2를 위해 물건2의 무게인 3만큼 자리를 만들어주자. dp[2][4]인 8에 물건 3의 value를 더하면, 물건 3을 가방에 넣을 때, 그리고 최대 무게가 7일 때 얻을 수 있는 최대 무게인 14가 된다.

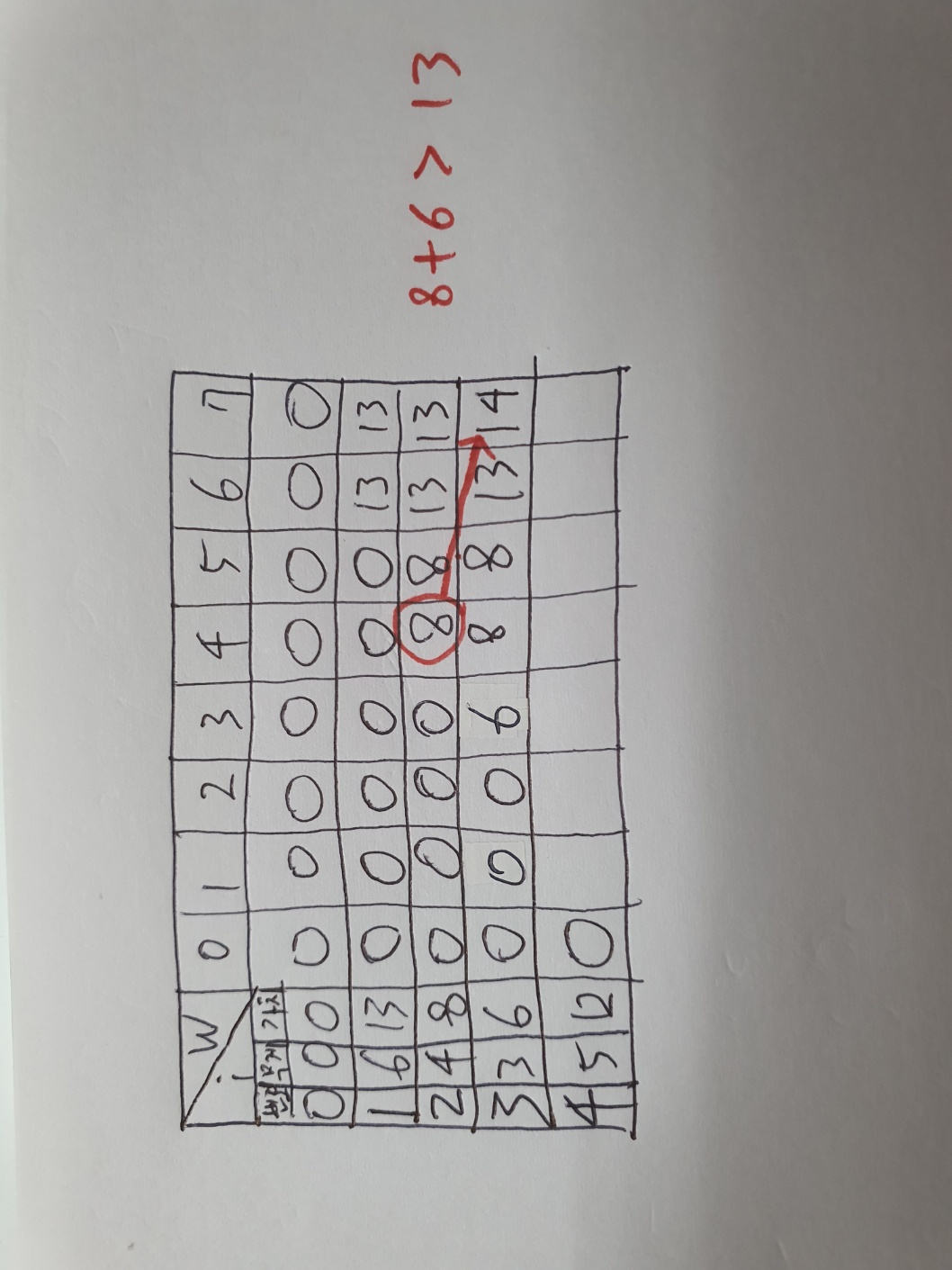
i가 4일 때도 같은 방식으로 채워나가면 아래와 같은 표가 완성된다.

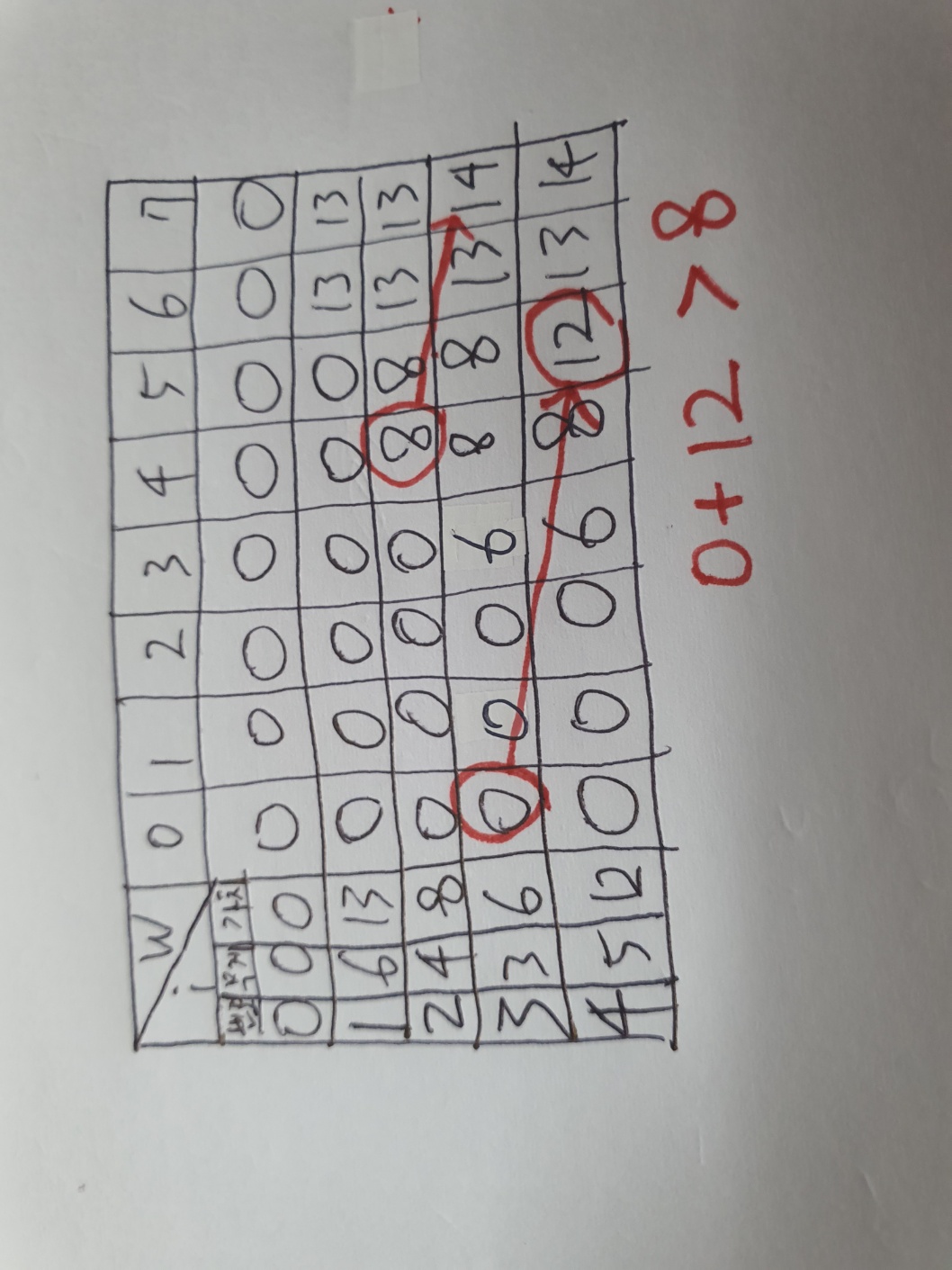
점화식

표의 칸(dp[i][w])을 하나씩 채울 때 선택지는 2개이다.

dp[i][w] = dp[i - 1][w]
또는
dp[i][w] = dp[i - 1][w - i번째 물건의 무게] + i번째 물건의 value

그래서 dp[i][w]는 저 위의 2개 중에 큰 값을 max 써서 고르면 되는 거 아닌가? 라고 단순하게 생각하기에는 w >= i번째 물건의 무게일 때만 2번째 수식을 사용할 수 있으므로 if로 조건 분기를 해야 한다. 그래서 소스 코드가 저렇게 나온 것이다.

그래서 점화식은?

$dp[i][w] = \begin{cases} dp[i-1][w] & \text{if } w < w_i \\\max(dp[i-1][w], dp[i-1][w-w_i] + v_i) & \text{if } w\geq w_i \end{cases}$

점화식을 도출했으니 코드로 옮기면 된다.

나의 코드

from sys import stdin as s

s = open("input.txt", "rt")  # 주석 처리해야 하는 부분

n, k = map(int, s.readline().split())

items = []
for _ in range(n):
    items.append(list(map(int, s.readline().split())))

dp = [[0] * (k + 1) for _ in range(n + 1)]

for i in range(1, n + 1):
    cur_weight, cur_value = items[i - 1]
    for w in range(1, k + 1):
        if w >= cur_weight:
            dp[i][w] = max(dp[i-1][w], dp[i-1][w - cur_weight] + cur_value)
        else:
            dp[i][w] = dp[i - 1][w]

print(dp[i][k])

어렵지만 새로운 개념을 알게되어서 재미있었다~ 다음에는 fractional knapsack도 풀어봐야지!! 짜이찌앤~~