1. 해시테이블과 해시함수
해시테이블
- 데이터 저장
: 데이터 → [ 해시함수 ] → (해시테이블상의) 주소 or 인덱스 ⇒ 그 주소로 가서 데이터를 저장!
- 데이터 조회
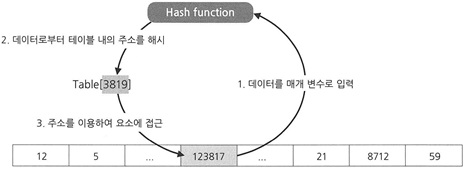
: 찾고자 하는 데이터 → [해시함수 ] → 주소값을 얻어서 ⇒ 그 주소로 가서 데이터를 조회!
▶ 즉, 해시테이블은
데이터를 담을 테이블을 미리 크게 확보하고 → 입력 받은 데이터를 해시하여 → 테이블 내의 주소를 계산해서 → 이 주소에 데이터를 담는 것이다.
- 시간복잡도 : O(1) → 해시함수만 한 번 하면 됨
- 데이터 접근에 있어서 배열과 비슷하다!
- 해시 테이블 성능 : 테이블상에 비어있는 여유 공간(이 많아야 성능 good)
해시함수
-
해시 : 다양한 길이를 가진 데이터를 고정된 길이를 가진 데이터로 매핑한 값 (잘게 부수고 다시 뭉친다.)
-
입력 값에서 테이블 내의 주소를 계산해 주는 함수
(즉, 임의의 길이를 갖는 데이터를 고정된 길이의 데이터로 변환시켜주는 함수)
-
주 용도 : 해시테이블(탐색 알고리즘 / 테이블 내 주소로 매핑), 암호화(데이터를 변형), 데이터 축약(큰 데이터 → 짧게)
-
해시함수 주소 계산 2가지
1) 나눗셈법
: 주소 = 입력값 % 테이블 크기
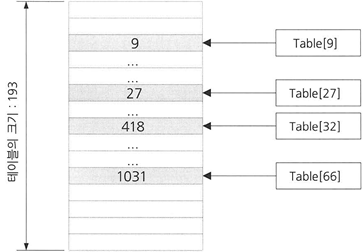
- 주소의 범위 : 0 ~ n-1 (테이블 크기 - 1)
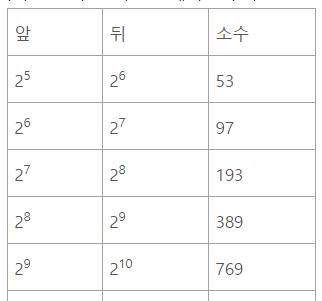
- 테이블 크기(n)을 소수로 정하는 것이 좋다.
- 특히 2의 제곱수와 거리가 먼 소수를 사용하면 함수의 성능이 높아진다.
- 장점 : 매우 간단한 알고리즘!
- 단점 : 동일한 주소값을 반환하는 경우, 해시테이블의 충돌이 발생한다. + 클러스터(테이블상의 특정 주소에 몰리는 경우)도 발생할 수 있다.
+구현 코드가 있다..!
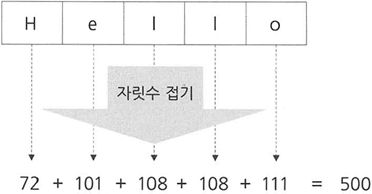
2) 자릿수 접기법
: 정해진 자릿수대로 끊고 더하여 → 숫자를 일정한 크기 이하의 수로 만듦
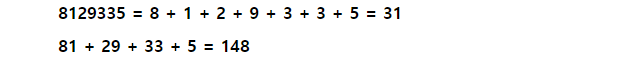
- 한자리씩 : 0 ~ 63 / 두자리씩 : 0 ~ 306 ⇒ 해시값을 얻을 수 있다.
(문자열의 경우, 각각의 문자를 아스키코드로 변환한 후 더한다. )
- 장점 : 나눗셈법의 단점을 보완(충돌을 줄일 뿐, 완전히 해소는 아님) + 극한의 성능을 자랑한다.
- 단점 : 메모리의 낭비를 초래할 수 있다. → 문자열의 경우, 10문자로 제한했을 때 10 * 127 = 1270이라서 0 ~ 1270까지의 주소만을 사용하게 될 텐데, 해시 테이블의 크기가 126456(그냥 막 누름..)이었다면 그 남은 만큼의 공간이 남아 도는 것. ⇒ 애초에 해시 함수를 구현할 때 남은 공간(비트)를 활용하는 방향으로 구현할 수 있다. (단점 보완!)
2. 해시 충돌 + 해결
해시함수는 어떠한 알고리즘을 갖고 설계되었다고 해도, 반환하는 주소가 겹치는 “해시 충돌”이 발생한다. 해시 충돌을 해결하는 방법으로는 두 가지가 있는데,
1) 개방 해싱 (Opening Hashing) : 체이닝 (Chaining)
2) 폐쇄 해싱 (Closed Hashing) : 개방 주소법 (Open Addressing)
하루살이 개발자