잠깐..! 스택 / 큐 / 리스트 각각이 무슨 차이인지 한 번에 이해해 보자!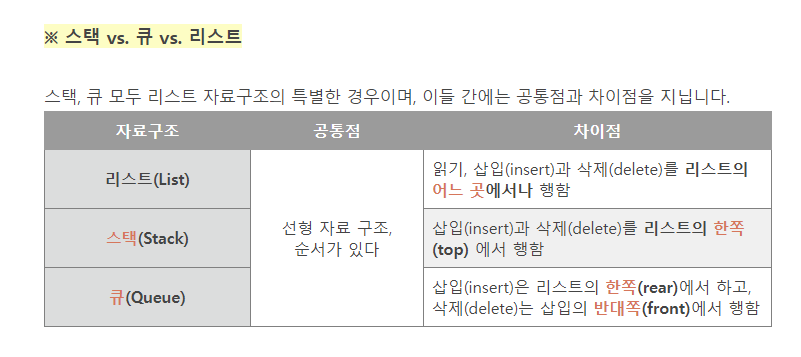 
1. 스택 (Stack)
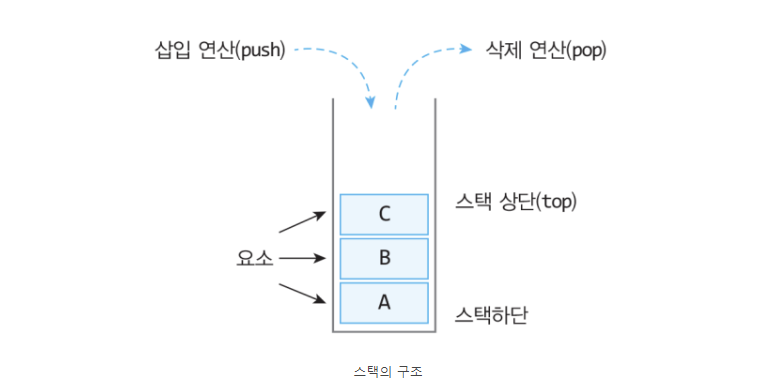
1) 개념
- 후입 선출 (LIFO : Last-In First-Out)
- top : 가장 최근에 들어온 자료 bottom : 가장 처음에 들어온 자료
- 스택 언더플로우 : 스택이 비어있는데, pop 하려고 하면! → 공백 스택
스택 오버플로우 : 스택이 꽉 차 있는데, push 하려고 하면! → 포화 스택(풀 스택)
- 용도
- 계산기, 후위 표기법, 재귀 구현 시 유용한 자료구조
- 대부분의 되돌리기(undo) 기능에도 사용
- 운영체제의 시스템 스택에도 사용됨 (함수 호출 시, 복귀주소 기억)
2) 스택 ADT (추상 자료형)
객체 : n개의 element(요소)들의 선형 리스트
연산 : 스택에 요소를 추가/삭제하는 연산과, 현재 스택 상태를 검사하는 연산들로 구성된다.
- init() : 스택 생성 + 초기화
- push(e) : 스택의 맨 위에 요소 e 추가
- pop(s) : 스택의 맨 위 요소 삭제
- peek(s) : 스택의 맨 위 요소를 삭제하지 않고 반환
- is_empty(s) : 스택이 비어있는지 검사
- is_full(s) : 스택이 가득 찼는지 검사
▶ 실제 기본 연산
peek(): 스택 맨 위의 데이터 반환 → 삭제 X (top함수로도 많이 쓴다.)push(): 스택에 데이터 삽입pop(): 스택에서 데이터 삭제하여 반환 → 삭제 Oisempty(): 스택에 원소가 없으면 ‘True’ 있으면 ‘False’ 반환isfull(): 스택에 원소가 가득하면 ‘True’ 가득하지 않으면 ‘False’ 반환
※ 스택 정적/동적 구현 → 1차원 배열/링크드 리스트 (C언어)
(출처 : https://roi-data.com/entry/자료구조-4-스택Stack이란-연산-구현방법)
3-1) 스택 구현 : 1차원 리스트 사용 (정적)
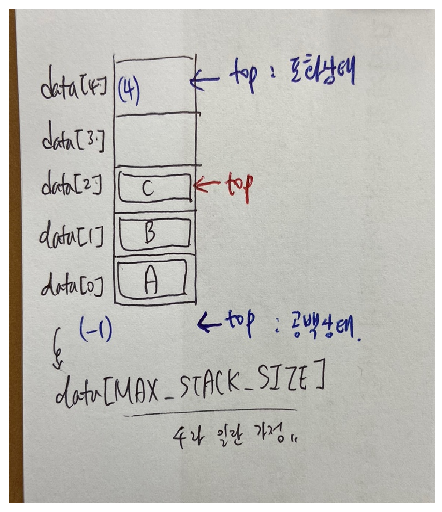
- 스택의 범위 : data[0] ~ data[top]
- 공백 상태 : -1 포화 상태 : top
# 1. 스택 생성
stack = [None for _ in range(MAX_SIZE = 5)]
top_pointer = -1
stack_size = 4
# 2. 스택 삽입 (push)
def push(n)-> None:
global top_pointer
if top_pointer + 1 >= stack_size:
print("stack overflow")
exit()
else:
top_pointer += 1
stack[top_pointer] = n
# 3. 스택 삭제 (pop)
def pop() -> None :
global top_pointer
del stack[top_pointer]
top_pointer -= 1
# 4. 스택 검사 (isempty / isfull)
def isempty() -> bool:
global top_pointer
if top_pointer < 0:
return True
else:
return False
def isfull() -> bool:
global top_pointer
if top_pointer == stack_size:
return True
else:
return False
def peek() -> int:
global top_pointer
return stack[top_pointer]3-2) 스택 구현 : 클래스 + 1차원 리스트 + 내장함수 사용 (동적)
class stack:
def __init__(self): # 1. 스택 객체 생성
self.items = []
def push(self, item): # 2. 스택 삽입 (push)
self.items.append(item)
def pop(self): # 3. 스택 삭제 후 리턴 (pop)
return self.items.pop()
def peek(self): # 4. 스택 맨 뒤 요소 리턴
return self.items[-1]
def isempty(self): # 5. 스택이 비었는지 확인 (비었으면 True 리턴)
return not self.items
stk = stack() # 스택 객체 생성
stk.push(1)
stk.push(2)
stk.push(3)
print(stk.items) # => [1,2,3]
print(stk.pop()) # => 3 (3 삭제하고 3을 출력함)
print(stk.items) # => [1,2]
print(stk.peek()) # => 2 (2 삭제 안 하고 2를 출력함)
print(stk.items) # => [1,2]
print(stk.pop())
print(stk.pop()) # 여기까지 해서, 스택은 빈 스택이 된다.
print(stk.isempty()) # 객체에 아무것도 없으므로 True 출력
print(stk.items) # 비어 있으므로 [] 출력3-3) 스택 규현 - deque 라이브러리 사용
공식문서 : https://docs.python.org/3.8/library/collections.html#collections.deque
from collections import deque
dq = deque() # 덱 생성
dq.apppend() # 덱의 가장 오른쪽에 원소 삽입
dq.popleft() # 가장 왼쪽 원소 반환
dq.appendleft() # 덱의 가장 왼쪽에 원소 삽입
dq.pop() # 가장 오른쪽 원소 반환
dq.clear() # 모든 원소 제거
dq.copy() # 덱 복사
dq.count(X) # x와 같은 원소의 개수를 계산2. 큐 (Queue)
1) 개념
- 큐는 '선착순'이다.
- FIFO(First-In First-Out) 규칙에 따라 데이터의 삽입과 삭제가 이뤄지는 순차적인 자료구조이다.
앞서 살펴본 스택과의 비교를 통해 큐를 설명하면 다음과 같다.
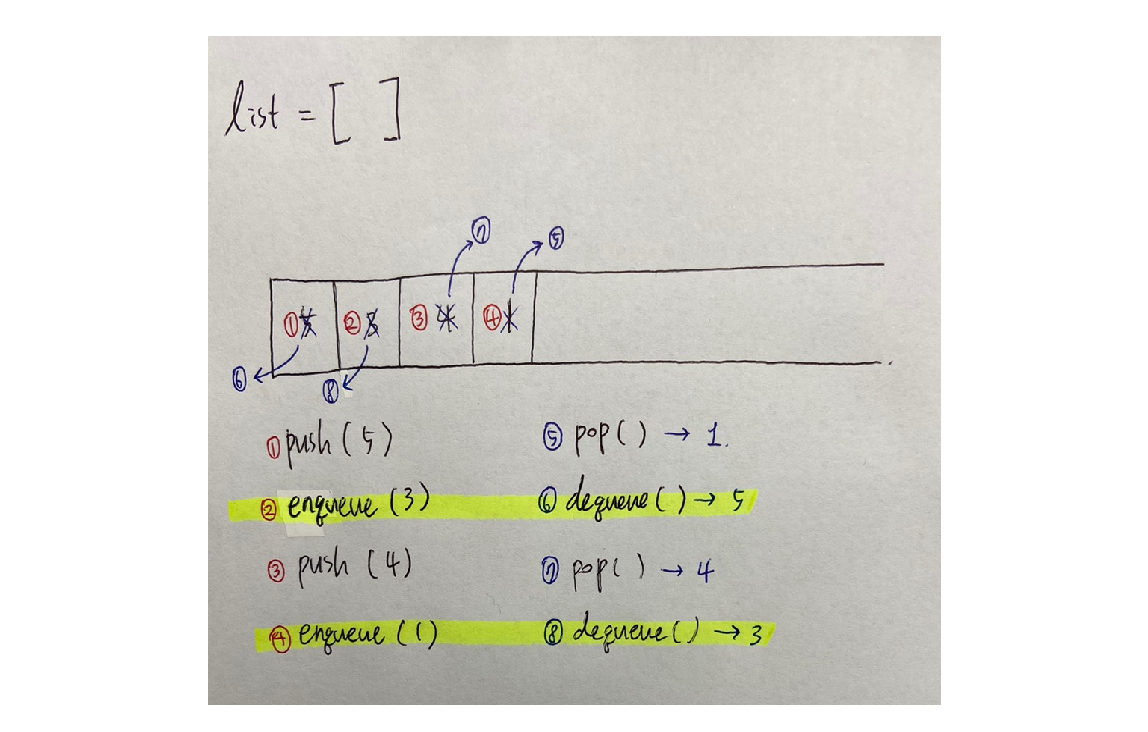
Insert (데이터 삽입) : 스택
push/ 큐enqueue
Delete (데이터 삭제) : 스택pop/ 큐dequeue
- 스택이 push와 pop을 수행하기 위해 필요한 정보는 한 가지이다.
:top→ 가장 마지막에 들어온 데이터의 위치(인덱스)만 알면 된다.- 큐가 enqueue와 dequeue를 수행하기 위해 필요한 정보는 두 가지이다.
:rear와front
→ 어느 인덱스로 들어와야 하는지(rear - enqueue) / 어느 인덱스로 나가야 하는지 (front - dequeue)
2) 큐 ADT (클래스)
객체 : items(list) / front_index(int)
※ rear와 front의 기능 모두front_index로 관리할 수 있다.
연산 : 큐 초기화 / enqueue / dequeue
class Queue:
def __init__(self):
self.items = [] # 빈 리스트
self.front_index = 0
def enqueue(self, val):
self.items.append(val)
def dequeue(self): # 리스트의 데이터 삭제 대신 인덱스의 이동으로 처리한다.
if self.front_index == len(self.itmes):
print("Queue is empty")
return None
else:
x = self.items[front_index]
front_index += 1
return x3) 선형 큐 & 원형 큐
보통은 큐를 구현할 때, 스택과 같이 '프링글스 통'으로 구현한다.
즉, 일자형 리스트(배열)의 형태로 큐의 구조와 기능을 정의하는데, 이를 '선형 큐'라고 한다.
그러나 일부 상황에서는 선형 큐가 단점을 갖기도 한다.
(길이가 고정된 리스트에서) 큐의 삽입과 삭제를 반복하다 보면, rear는 마지막 인덱스(n-1)에 위치하게 되고 이때 isFull()를 호출하면 True를 반환한다. front가 0이라면 맞는 리턴이지만, 만약 front가 0이 아닌 다른 인덱스에 위치한다면 틀린 리턴이다. 즉, 오류다.
이를 그림으로 이해해 보자면 다음과 같다.
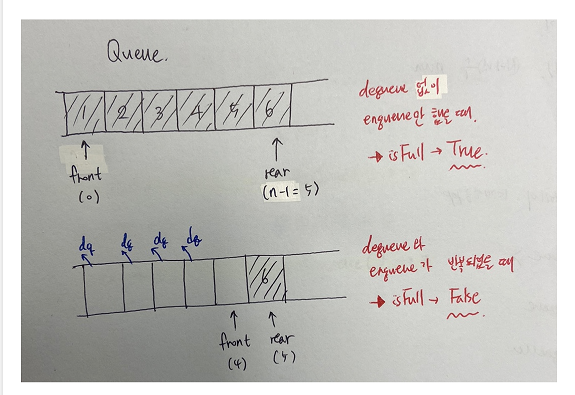오류가 생기는 이유는,
데이터가 dequeue 될 때마다 남은 원소들을 한 칸씩 앞으로 이동시키지 않고, front 포인터만 이동 시켜 큐의 연산을 진행했기 때문이다. (즉, front 앞에 있는 값들은 없는 걸로 치부한다.)
이와 같은 선형 큐의 단점을 보완하기 위해 나온 것이 바로 '원형 큐'이다.
(즉, 데이터 dequeue 후 기존의 데이터 이동 없이도, dequeue 된 공간을 지속적으로 활용할 수 있는 방안에 대한 해결책으로 원형 큐가 등장하였다.)
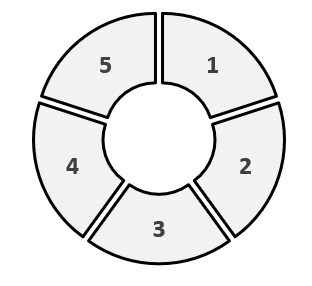원형 큐는 선형 큐와 마찬가지로 1차원 배열(리스트)를 사용하지만, 추상적으로 원형의 구조를 가진다고 생각하면 된다.
원형 큐의 특징과 연산을 정리해 보자면,
- 원형 큐도 1차원 배열(리스트)로 구현한다.
front와rear모두 첫 인덱스부터 시작한다.
front는 비어 있는 위치(인덱스)를 나타낸다.rear는 top에 있는 원소의 위치(인덱스)이다.- isEmpty() / isFull() 함수가 필요 없다.
→ 데이터 삽입, 삭제 시 큐가 full 혹은 empty인지 먼저 확인할 수 있도록 한다.- 입력 데이터의 크기가 n이라면, 1차원 배열의 크기를 n + 1로 설정한다.
- 데이터의 삽입(enqueue) 시, rear가 +1이 되고 → 해당 인덱스에 데이터를 넣는다.
rear = (rear + 1) % (n + 1)
→ 0 ~ n + 1 범위에서 rear가 1씩 증가하는 것- 만약
(1 증가된) rear == front라면, 큐는 Full이다.- 데이터의 삭제(dequeue) 시, front가 +1이 되고 → 해당 인덱스에 있는 데이터를 별도로 떼어 놓는다. (front가 위치한다는 것은 빈칸이라는 의미)
front = (front + 1) % (n + 1)
→ 0 ~ n + 1 범위에서 front가 1씩 증가하는 것- 만약
rear == front라면, 큐는 Empty이다.
원형 큐는 다음과 같이 구현할 수 있다.
1) CircularQueue.py
n = 10 # 입력 데이터의 크기가 10이라고 가정한다.
queue = [0] * (n+1)
front, rear = 0, 0
def enQueue(data: int) -> None:
global front, rear
if (rear+1) % (n+1) == front:
print("Q if full")
return
rear = (rear+1) % (n+1)
queue[rear % (n+1)] = data
def deQueue() -> None:
global front, rear
if rear == front:
print("Q is empty")
return
data = queue[(front+1) % (n+1)]
front = (front+1) % (n+1)
def printQueue() -> None:
global front, rear
idx = (front+1) % (n+1)
while True:
if front == rear:
print('Q is empty')
break
elif idx > rear:
break
idx += 1
print(f"{queue[(idx) % (n+1)]} ")
2) CircularQueue.cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
int count = 0;
int n;
int front = 0, rear = 0;
int* queue;
void enQueue(int data) {
if((rear+1) % (n+1) == front){
printf("Q is full\n");
return;
}
rear = (rear+1) % (n+1);
queue[rear % (n+1)] = data;
}
int deQueue() {
int data;
if(front == rear){
printf("Q is empty\n");
return;
}
data = queue[(front+1) % (n+1)];
front = (front+1) % (n+1);
}
void printQueue() {
int idx = 0;
idx = (front+1) % (n+1);
do{
if(front == rear){
printf("Q is empty\n");
break;
}
else if(idx > rear) break;
printf("%d ", queue[idx++ % (n+1)]);
} while(1);
}
int main(){
printf("원형 큐의 크기 입력: ");
scanf("%d", &n);
queue = (int*)malloc(sizeof(int) * (n+1));
while(1) {
int menu, data;
printf("\n1. 삽입, 2. 삭제, 3. 출력, 4. 종료\n");
scanf("%d", &menu);
switch(menu)
{
case 1:
printf("삽입할 데이터 입력: ");
scanf("%d", &data);
enQueue(data);
break;
case 2:
deQueue();
break;
case 3:
printQueue();
break;
case 4:
exit(1);
break;
}
}
return 0;
}3. 우선순위 큐 (Priority Queue)
1) 개념
“우선순위 큐는 힙의 구조를 가진다.”
(스택과 큐가 ‘리스트’라면, 우선순위 큐는 ‘힙’의 구조로 생각하면 된다.)
- 힙(완전이진트리)로서, 최대 힙 혹은 최소 힙의 구조를 가진다.
- 각각의 원소들은 ‘우선순위’를 가지고 있다.
- 큐의 기본 원리를 가지고 가되 + 우선순위가 높으면 그 원소부터 먼저 처리!
step 1. 우선순위 높은 원소가!
step 2. (우선순위가 같다면) 먼저 들어온 원소가! → FIFO
※ 힙이란?
- 완전이진트리의 형태로 이루어져 있다.
- 부모노드와 서브트리간 대소 관계가 성립된다.
- 이진탐색트리(BST)와 달리 중복된 값이 허용된다.
- ★ 이진탐색트리(BST)와 달리, 왼쪽/오른쪽 대소관계가 필요 없다.
(부모노드가 양쪽 자식보다는 커야 함 + 왼쪽 자식이 오른쪽 자식보다 더 커도 됨)- 최대힙 : 부모노드의 키 값이 자식노드의 키 값보다 크거나 같은 완전이진트리
- 최소힙 : 부모노드의 키 값이 자식노드의 키 값보다 작거나 같은 완전이진트리
(우선순위 큐를 힙 외에도 배열과 리스트로 구현할 수도 있다. 다만, 시간복잡도가 저리 되다 보니..힙을 사용한다.)
- 힙 트리의 높이 : log(N+1) / 시간복잡도 : O(logN)
- 탐색에 적용하기보다는, 정렬 혹은 최대 최소값 찾는 데에 유용한 자료구조라고 보면 된다.
- 노드는 왼쪽부터 채워지기 때문에 이 순서만 갖고 있다면, push 혹은 pop 되어도 완전이진트리를 유지한다.
2) 우선순위 큐 ADT (클래스)
우선순위 큐의 ADT (클래스)
객체 : 우선순위를 가진 요소들의 모임
연산
1. insert(x) : 우선순위 큐에 요소 x 추가
2. remove() : 우선순위 큐에서 가장 우선순위가 높은 요소를 삭제하고 반환
3. find() : 우선순위 큐에서 가장 우선순위가 높은 요소를 반환
(공부하면서 느낀 거지만, 힙 정렬과 완전히 맞닿아 있는 것 같다.)
삽입 연산 : insert(x)
- 삽입할 요소를 (새로운 노드로 만들어) 트리의 마지막 노드 다음에 넣는다.
- 새로운 노드가 부모 노드보다 크다면, 부모와 자식 노드를 swap 한다.
- 앞선 과정을 반복하여, 새로운 노드를 (힙 트리를 만족하는) 인덱스로 위치 시킨다.
이때, 삽입 연산의 시간복잡도는 O(logN)이다. (최악의 경우, 루트 노드까지 올라가야 하므로)
삭제연산 : remove()
힙 트리에서 루트 노드가 가장 우선순위가 높으므로 루트 노드부터 삭제한다.
루트 노드를 삭제하면, 남은 노드들을 가지고 힙 트리를 유지하기 위해 재정렬을 시도한다.
- 루트 노드를 삭제한다.
- 마지막 노드를 루트 노드로 올린다.
- 루트 자리에 위치한 마지막 노드를 자식 노드들과 비교하여, 제 위치에 갖다 놓는다.
(최대 힙인 경우 부모 > 자식 / 최소 힙인 경우 부모 < 자식의 형태가 되어야 한다.) - 위의 과정을 반복하여, 더 이상 부모와 자식간의 교환이 필요없는 정상적인 힙 트리로 재정렬한다.
삽입 연산과 마찬가지로, 삭제 연산 또한 시간복잡도가 O(logN)이 나온다.
잠깐..! 구현으로 넘어가기 전에, 힙 트리는 부모와 자식의 위치를 쉽게 구할 수 있는데 (루트 노드를 0부터 지정했다는 가정 하에)
👶 자식 노드의 인덱스를 구하는 방법은
- 왼쪽 자식 : 부모 노드(인덱스) * 2 + 1
- 오른쪽 자식 : 부모 노드(인덱스) * 2 + 2
🤱 부노 노드의 인덱스를 구하는 방법은
- 왼쪽 자식을 알 때 : 왼쪽 자식 노드(인덱스) // 2
- 오른쪽 자식을 알 때 : 오른쪽 자식 노드(인덱스) - 1 // 2
로 쉽게 구할 수 있다. (힙 소트에서 힙을 정렬할 때 많이 사용한다.)
3) 구현
우선순위 큐가 완전이진트리이다 보니, 중간 중간 비어 있는 요소가 없기 때문에 주로 배열(리스트)로 구현한다.
4) 응용 예제 : 힙 정렬
힙의 삭제/삽입은 각각 O(logN)이 걸린다고 했다.
따라서, 힙 정렬은 n개의 원소에 대해 n번의 삽입과 n번의 삭제가 이뤄지므로 정렬에 필요한 시간 복잡도는
logN + logN에 비례한다고 할 수 있다.
추가로, 최대값/최대값 찾을 때 → 최대힙/최소힙 사용해서 루트만 꺼내면 된다. O(1)
더 자세한 설명은 👉 WEEK01 WIL 2-3.정렬 여기에 정리해 놓았다.
5) 구현 : PriorityQueue 모듈
우선순위 큐를 쉽게 구현하는 방법으로는 PriorityQueue 모듈을 사용하는 방법이 있다.
- 클래스 임포트
from queue import PriorityQueue- 우선순위 큐 생성
que = PriorityQueue()
que = PriorityQueue(maxsize=10) # 디폴트 사이즈는 무한대이다. maxsize로 최대 크기를 지정할 수 있다.- 우선순위 큐에 원소 추가 :
put()
que.put(4)- 우선순위 큐에 원소 삭제 :
get()
que.get() # get()은 삭제된 원소를 리턴하므로, print()로 씌어서 삭제되는 원소를 출력할 수 있다.- 정렬 기준 변경
오름차순이 아닌, 다른 기준으로 원소를 정렬하고 싶으면 (우선순위, 값) 튜플의 형태로put(삽입) /get(삭제) 할 수 있다.
que.put((3, '장서영'))
que.put((2, '짱구'))
que.put((1, '뽀로로'))
print(que.get()[1]) # 뽀로로
print(que.get()[1]) # 짱구
print(que.get()[1]) # 장서영추가로, 백준 문제를 풀면서 더 알게 된 것은
- PriorityQueue 모듈을 사용했을 때, 큐가 비어 있는지 확인하는 방법은
.empty()를 호출하면 된다. (비어 있을 시, True 반환) - PriorityQueue(모듈)은 데이터를 추가(put)한 순서에 상관 없이 데이터를 꺼낼 때(get) 값을 오름차순하여 반환한다.
- 따라서, 결과를 역순(내림차순)으로 반환하고 싶다면, 튜플 형태로 값을 get/put 하면 된다.
ex)que.put((-num, num))삽입 →que.get()[1]삭제
6) 구현 : Heapq 모듈
heqpq 모듈을 사용해 우선순위 큐를 빠르게 사용할 수 있다.
-> https://docs.python.org/ko/3/library/heapq.html
추가로, PriorityQueue와 Heapq 모듈을 비교해 놓았다.
-> https://slowsure.tistory.com/130
💡 자료구조 연산 구현 시,
- 리스트(혹은 1차원 배열)의 크기를 지정한다. -> 아니면 무작정 크기를 많이 할당하기 때문
pop()은 del 혹은 remove를 하지 말 것.. (데이터 자체를 건드리기보다는 포인터로 처리하는 게 더 좋다고 한다.)
