특잇값 분해

Jane의 study note.·2022년 10월 10일

선형대수

목록 보기

9/9

정방행렬은 고유분해로 고윳값과 고유벡터를 찾을 수 있었다. 정방행렬이 아닌 행렬은 고유분해가 불가능하다. 하지만 대신 고유분해와 비슷한 특이분해를 할 수 있다.

1. 특잇값과 특이벡터

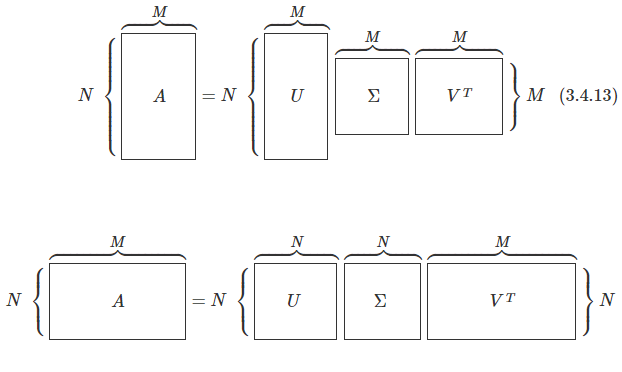
$N \times M$ 크기의 행렬 $A$ 를 다음과 같은 3개의 행렬의 곱으로 나타내는 것을 특이분해(singular-decomposition) 또는 특잇값 분해(singular value decomposition)라고 한다.

A = U\Sigma V^T

여기에서 $U, \Sigma, V$ 는 다음 조건을 만족해야 한다.

대각성분이 양수인 대각행렬이어야 한다. 큰 수부터 작은 수 순서로 배열한다.

\Sigma \in \mathbf{R}^{N \times M}

$U$ 는 $N$ 차원 정방행렬로 모든 열벡터가 단위벡터이고 서로 직교해야 한다.

U \in \mathbf{R}^{N \times N}

$V$ 는 $M$ 차원 정방행렬로 모든 열벡터가 단위벡터이고 서로 직교해야 한다.

V \in \mathbf{R}^{M \times M}

위 조건을 만족하는 행렬 $\Sigma$ 의 대각성분들을 특잇값(singular value), 행렬 $U$ 의 열벡터들을 왼쪽 특이벡터(left singular vector), 행렬 $V$ 의 행벡터들을 오른쪽 특이벡터(right singular vector)라고 부른다.

[정리] 특이분해는 모든 행렬에 대해 가능하다. 즉 어떤 행렬이 주어지더라도 위와 같이 특이분해할 수 있다.

증명은 이 책의 범위를 벗어나므로 생략한다.

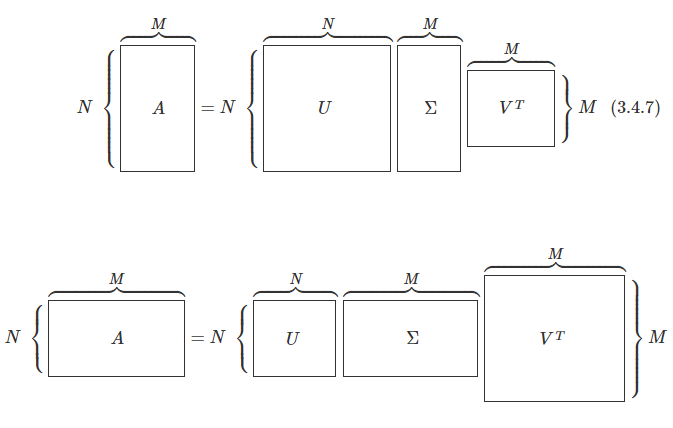
2. 특이값 분해 행렬의 크기

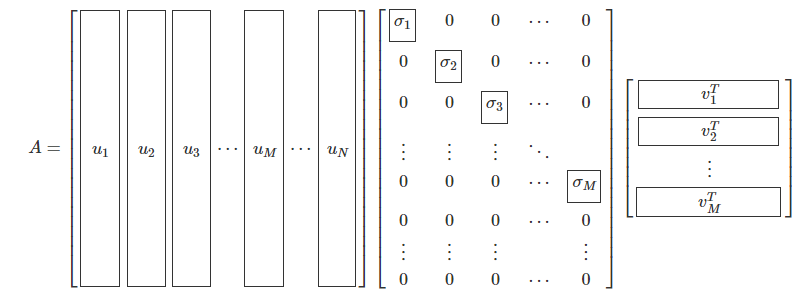
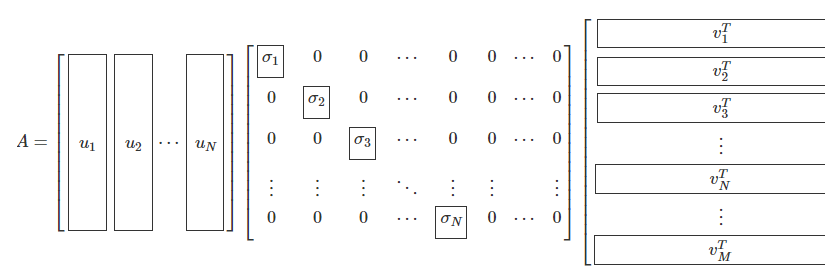
특잇값의 개수는 행렬의 열과 행의 개수 중 작은 값과 같다. 특이분해된 형태를 구체적으로 쓰면 다음과 같다.
만약 $N > M$ 이면 $\Sigma$ 행렬이 $M$ 개의 특잇값(대각성분)을 가지고 다음처럼 아랫 부분이 영행렬이 된다.

반대로 $N < M$ 이면 $\Sigma$ 행렬이 $N$ 개의 특잇값(대각성분)을 가지고 다음처럼 오른쪽 부분이 영행렬이 된다.
행렬의 크기만 표시하면 다음과 같다.

3. 특잇값 분해의 축소형

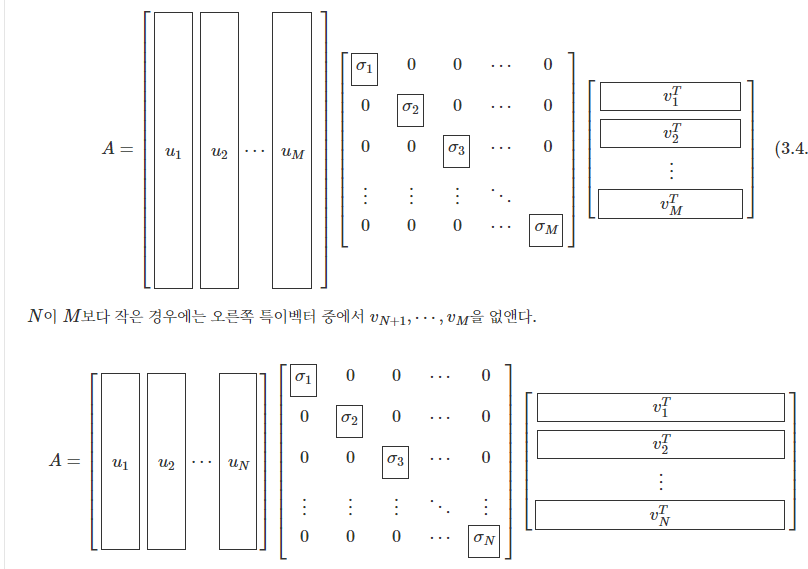
특잇값 대각행렬에서 0인 부분은 사실상 아무런 의미가 없기 때문에 대각행렬의 0 원소 부분과 이에 대응하는 왼쪽(혹은 오른쪽) 특이벡터들을 없애고 다음처럼 축소된 형태로 해도 마찬가지로 원래 행렬이 나온다.

$N$ 이 $M$ 보다 큰 경우에는 왼쪽 특이벡터 중에서 $u_{M+1}, \cdots, u_N$ 을 없앤다.

4. 파이썬을 사용한 특이분해

numpy.linalg 서브패키지와 scipy.linalg 서브패키지에서는 특이분해를 할 수 있는 svd() 명령을 제공한다. 오른쪽 특이행렬은 전치행렬로 출력된다는 점에 주의하라.

from numpy.linalg import svd

A = np.array([[3, -1], [1, 3], [1, 1]])
U, S, VT = svd(A)

5. 특잇값과 특이벡터의 관계

행렬 $V$ 는 정규직교(orthonormal)행렬이므로 전치행렬이 역행렬이다.

V^T = V^{-1}

특이분해된 등식의 양변에 $V$ 를 곱하면,

AV = U\Sigma V^TV = U\Sigma

A \begin{bmatrix} v_1 & v_2 & \cdots & v_M \end{bmatrix} = \begin{bmatrix} u_1 & u_2 & \cdots & u_N \end{bmatrix} \begin{bmatrix} \sigma_1 & 0 & \cdots \\ 0 & \sigma_2 & \cdots \\ \vdots & \vdots & \ddots \\ \end{bmatrix}

행렬 $A$ 를 곱하여 정리하면 $M$ 이 $N$ 보다 클 때는

\begin{bmatrix} Av_1 & Av_2 & \cdots & Av_N \end{bmatrix} = \begin{bmatrix} \sigma_1u_1 & \sigma_2u_2 & \cdots & \sigma_Nu_N \end{bmatrix}

이 되고 $N$ 이 $M$ 보다 클 때는

\begin{bmatrix} Av_1 & Av_2 & \cdots & Av_M \end{bmatrix} = \begin{bmatrix} \sigma_1u_1 & \sigma_2u_2 & \cdots & \sigma_Mu_M \end{bmatrix}

이 된다.

즉, $i$ 번째 특잇값 $\sigma_i$ 와 특이벡터 $u_i$ , $v_i$ 는 다음과 같은 관계가 있다.

Av_i = \sigma_i u_i \;\; (i=1, \ldots, \text{min}(M,N))

이 관계는 고유분해와 비슷하지만 고유분해와는 달리 좌변과 우변의 벡터가 다르다.

6. 특이분해와 고유분해의 관계

행렬 $A$ 의 분산행렬 $A^TA^{}$ 는

A^TA^{} = (V^{} \Sigma^T U^T)( U^{}\Sigma^{} V^T) = V^{} \Lambda^{} V^T

가 되어 행렬 $A$ 의 특잇값의 제곱(과 0)이 분산행렬 $A^TA^{}$ 의 고유값, 행렬 $A$ 의 오른쪽 특이벡터가 분산행렬 $A^TA^{}$ 의 고유벡터가 된다.

위 식에서 $\Lambda$ 은 $N$ 이 $M$ 보다 크면

\Lambda = \begin{bmatrix} \sigma_1^2 & 0 & \cdots & 0 \\ 0 & \sigma_2^2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_M^2 \\ \end{bmatrix}

이고 $N$ 이 $M$ 보다 작으면

\Lambda = \begin{bmatrix} \sigma_1^2 & 0 & \cdots & 0 & \cdots & 0 \\ 0 & \sigma_2^2 & \cdots & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & \sigma_N^2 & \cdots & 0 \\ \vdots & \vdots & \cdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & \cdots & 0 \\ \end{bmatrix} = \text{diag}(\sigma_1^2, \sigma_2^2, \cdots, \sigma_N^2, 0, \cdots, 0)

이다.

마찬가지 방법으로 행렬 $A$ 의 왼쪽 특이벡터가 행렬 $AA^T$ 의 고유벡터가 된다는 것을 증명할 수 있다.

7. 1차원 근사

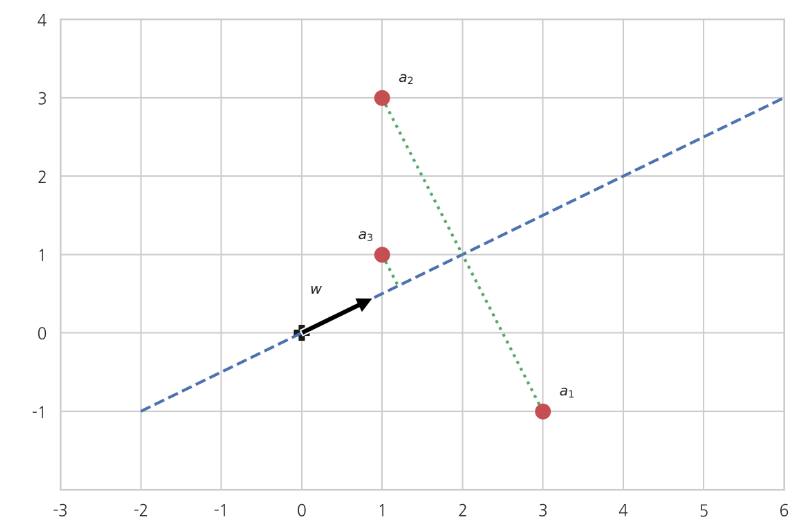
2차원 평면 위에 3개의 2차원 벡터 $a_1, a_2, a_3$ 가 있다. 원점을 지나면서 모든 점들과 가능한 한 가까이 있는 직선을 만들고 싶다면 직선의 방향을 어떻게 해야 할까? 직선의 방향을 나타내는 단위 벡터를 $w$ 라고 하자.

벡터 $w$ 와 점 $a_i$ 의 거리의 제곱은 다음처럼 계산할 수 있다.(연습 문제 3.1.9)

\Vert a_i^{\perp w}\Vert^2 = \Vert a_i\Vert^2 - \Vert a_i^{\Vert w}\Vert^2 = \Vert a_i\Vert^2 - (a_i^Tw)^2

벡터 $a_1, a_2, a_3$ 를 행벡터로 가지는 행렬 $A$ 를 가정하면

A = \begin{bmatrix} a_1^T \\ a_2^T \\ a_3^T \end{bmatrix}

행벡터의 놈의 제곱의 합은 행렬의 놈이므로 모든 점들과의 거리의 제곱의 합은 행렬의 놈으로 계산된다. (연습 문제 2.3.2)

\begin{aligned} \sum_{i=1}^3 \Vert a_i^{\perp w}\Vert^2 &= \sum_{i=1}^3 \Vert a_i\Vert^2 - \sum_{i=1}^3 (a_i^Tw)^2 \\ &= \Vert A \Vert^2 - \Vert Aw\Vert^2 \\ \end{aligned}

점 $a_i$ 의 위치가 고정되어 있으므로 행렬 $A$ 의 놈 값은 고정되어 있다. 따라서 이 값이 가장 작아지려면 $\Vert Aw\Vert^2$ 의 값이 가장 크게 만드는 $w$ 를 찾아야 한다.이 문제는 다음처럼 수식으로 쓸 수 있다.

\arg\max_w \Vert Aw \Vert^2

8. 1차원 근사의 풀이

벡터 $w$ 와 점 $a_i$ 의 거리의 제곱은 다음처럼 계산할 수 있다.(연습 문제 3.1.9)

\Vert a_i^{\perp w}\Vert^2 = \Vert a_i\Vert^2 - \Vert a_i^{\Vert w}\Vert^2 = \Vert a_i\Vert^2 - (a_i^Tw)^2

벡터 $a_1, a_2, a_3$ 를 행벡터로 가지는 행렬 $A$ 를 가정하면

A = \begin{bmatrix} a_1^T \\ a_2^T \\ a_3^T \end{bmatrix}

행벡터의 놈의 제곱의 합은 행렬의 놈이므로 모든 점들과의 거리의 제곱의 합은 행렬의 놈으로 계산된다. (연습 문제 2.3.2)

\begin{aligned} \sum_{i=1}^3 \Vert a_i^{\perp w}\Vert^2 &= \sum_{i=1}^3 \Vert a_i\Vert^2 - \sum_{i=1}^3 (a_i^Tw)^2 \\ &= \Vert A \Vert^2 - \Vert Aw\Vert^2 \\ \end{aligned}

\arg\max_w \Vert Aw \Vert^2

위에서 예로 든 행렬 $A \in \mathbf{R}^{3 \times 2}$ 를 특이분해하면 2개의 특잇값, 왼쪽/오른쪽 특이벡터를 가진다. 이를 각각 다음처럼 이름붙인다.

첫 번째 특잇값: $\sigma_1$ , 첫 번째 왼쪽 특이벡터 $u_1 \in \mathbf{R}^{3}$ , 첫 번째 오른쪽 특이벡터 $v_1 \in \mathbf{R}^{2}$
두 번째 특잇값: $\sigma_2$ , 두 번째 왼쪽 특이벡터 $u_2 \in \mathbf{R}^{3}$ , 두 번째 오른쪽 특이벡터 $v_2 \in \mathbf{R}^{2}$

첫 번째 특잇값 $\sigma_1$ 은 두 번째 특잇값 $\sigma_2$ 보다 같거나 크다.

\sigma_1 \geq \sigma_2

또한 위에서 알아낸 것처럼 A에 오른쪽 특이벡터를 곱하면 왼쪽 특이벡터 방향이 된다.

A v_1 = \sigma_1 u_1

A v_2 = \sigma_2 u_2

오른쪽 특이벡터 $v_1, v_2$ 는 서로 직교하므로 (같은 방향이 아니라서) 선형독립이고 2차원 평면공간의 기저벡터가 될 수 있다.

우리는 $\Vert Aw\Vert$ 의 값이 가장 크게 만드는 $w$ 를 찾아야 하는데 $w$ 는 2차원 벡터이므로 2차원 평면공간의 기저벡터인 $v_1, v_2$ 의 선형조합으로 표현할 수 있다.

w = w_{1} v_1 + w_{2} v_2

단, $w$ 도 단위벡터이므로 $w_{1}, w_{2}$ 는 다음 조건을 만족해야 한다.

w_{1}^2 + w_{2}^2 = 1

이때 $\Vert Aw\Vert$ 의 값은

\begin{aligned} \Vert Aw\Vert^2 &= \Vert A(w_{1} v_1 + w_{2} v_2)\Vert^2 \\ &= \Vert w_{1}Av_1 + w_{2}Av_2 \Vert^2 \\ &= \Vert w_{1} \sigma_1 u_1 + w_{2} \sigma_2 u_2 \Vert^2 \\ &= \Vert w_{1} \sigma_1 u_1 \Vert^2 + \Vert w_{2} \sigma_2 u_2 \Vert^2 \;\; \text{(orthogonal)} \\ &= w_{1}^2 \sigma_1^2 \Vert u_1 \Vert^2 + w_{2}^2 \sigma_2^2 \Vert u_2 \Vert^2 \\ &= w_{1}^2 \sigma_1^2 + w_{2}^2 \sigma_2^2 \;\; \text{(unit vector)}\\ \end{aligned}

$\sigma_1 > \sigma_2 > 0$ 이므로 $w_{1}^2 + w_{2}^2 = 1$ 라는 조건을 만족하면서 위 값을 가장 크게 하는 $w_{1}, w_{2}$ 값은

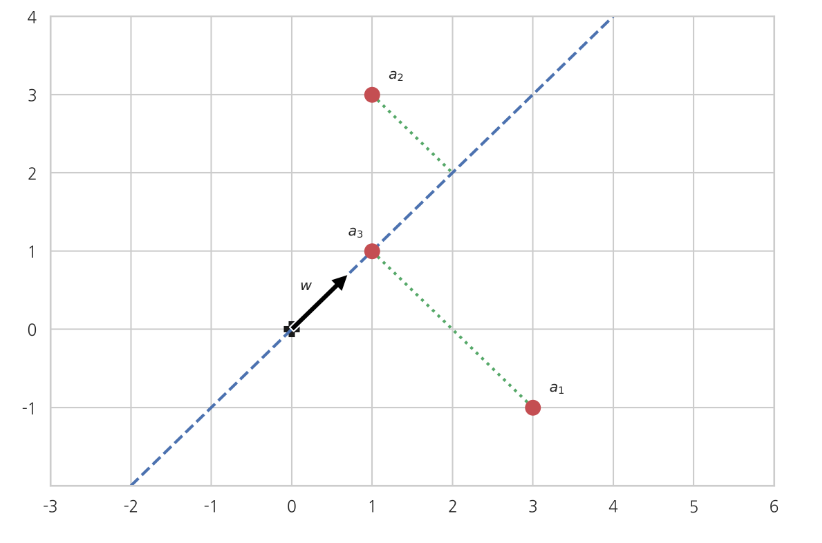
w_{1} = 1, w_{2} = 0

이다. 즉, 첫 번째 오른쪽 특이벡터 방향으로 하는 것이다.

w = v_1

이때 $\Vert Aw\Vert$ 는 첫 번째 특잇값이 된다.

\Vert Aw\Vert = \Vert Av_1\Vert = \Vert \sigma_1 u_1\Vert = \sigma_1 \Vert u_1\Vert = \sigma_1

위에서 예로 들었던 행렬

A = \begin{bmatrix} 3 & -1 \\ 1 & 3 \\ 1 & 1 \end{bmatrix}

첫 번째 오른쪽 특이벡터

v_1 = \begin{bmatrix} \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} \\ \end{bmatrix}

가 가장 거리의 합이 작은 방향이 된다. 그리고 이때의 거리의 제곱의 합은 다음과 같다.

\Vert A \Vert^2 - \Vert Aw\Vert^2 =\Vert A \Vert^2 - \sigma_1^2

만약 $N=3$ 이 아니라 일반적인 경우에는 다음처럼 풀 수 있다.

\begin{aligned} \Vert Aw \Vert^2 &= \sum_{i=1}^{N} (a_i^Tw)^2 \\ &= \sum_{i=1}^{N} (a_i^Tw)^T(a_i^Tw) \\ &= \sum_{i=1}^{N} w^Ta_ia_i^Tw \\ &= w^T \left( \sum_{i=1}^{N} a_ia_i^T \right) w \\ &= w^T A^TA w \\ \end{aligned}

분산행렬의 고유분해 공식을 이용하면,

\begin{aligned} w^T A^TA w &= w^T V \Lambda V^T w \\ &= w^T \left( \sum_{i=1}^{M} \sigma^2_iv_iv_i^T \right) w \\ &= \sum_{i=1}^{M}\sigma^2_i(w^Tv_i)(v_i^Tw) \\ &= \sum_{i=1}^{M}\sigma^2_i\Vert v_i^Tw\Vert^2 \\ \end{aligned}

이 된다. 이 식에서 $M$ 은 0이 아닌 특잇값 개수다.

즉, 우리가 풀어야 할 문제는 다음과 같다.

\arg\max_w \Vert Aw \Vert^2 = \arg\max_w \sum_{i=1}^{M}\sigma^2_i\Vert v_i^Tw\Vert^2

이 값을 가장 크게 하려면 $w$ 를 가장 큰 특잇값에 대응하는 오른쪽 고유벡터 $v_1$ 으로 해야 한다.

9. 랭크-1 근사문제

또 $a_i$ 를 $w$ 에 투영한 벡터는

a^{\Vert w}_i = (a_i^Tw)w

이므로 $w$ 벡터를 이용하면 $N$ 개의 $M$ 차원 벡터 $a_1, a_2, \cdots, a_N\;(a_i \in \mathbf{R}^M)$ 를 1차원으로 투영(projection)하여 가장 비슷한 $N$ 개의 1차원 벡터 $a^{\Vert w}_1, a^{\Vert w}_2, \cdots, a^{\Vert w}_N\;(a^{\Vert w}_i \in \mathbf{R}^1)$ 를 만들 수 있다.

A'= \begin{bmatrix} \left(a^{\Vert w}_1\right)^T \\ \left(a^{\Vert w}_2\right)^T \\ \vdots \\ \left(a^{\Vert w}_N\right)^T \end{bmatrix} = \begin{bmatrix} a_1^Tw^{}w^T \\ a_2^Tw^{}w^T \\ \vdots \\ a_N^Tw^{}w^T \end{bmatrix} = \begin{bmatrix} a_1^T \\ a_2^T \\ \vdots \\ a_N^T \end{bmatrix} w^{}w^T = Aw^{}w^T

이 답은 원래 행렬 $A$ 에 랭크-1 행렬 $w^{}w^T$ 를 곱해서 원래의 행렬 $A$ 와 가장 비슷한 행렬 $A'$ 을 만드는 문제와 같다.

\arg\min_w \Vert A - A' \Vert = \arg\min_w \Vert A^{} - A^{}w^{}w^T \Vert

따라서 문제를 랭크-1 근사문제(rank-1 approximation problem)라고도 한다.

10. K차원 근사

이번에는 $N$ 개의 $M$ 차원 벡터 $a_1, a_2, \cdots, a_N\;(a_i \in \mathbf{R}^M)$ 를 1차원이 아니라 정규직교인 기저벡터 $w_1, w_2, \cdots, w_K$ 로 이루어진 $K$ 차원 벡터공간으로 투영하여 가장 비슷한 $N$ 개의 $K$ 차원 벡터 $a^{\Vert w}_1, a^{\Vert w}_2, \cdots, a^{\Vert w}_N\;$ 를 만들기 위한 정규직교 기저벡터 $w_1, w_2, \cdots, w_K$ 를 찾는 문제를 생각하자. 이 문제는 랭크- $K$ 근사문제라고 한다.

기저벡터행렬을 $W$ 라고 하자.

W = \begin{bmatrix} w_1 & w_2 & \cdots & w_K \end{bmatrix}

정규직교 기저벡터에 대한 벡터 $a_i$ 의 투영 $a^{\Vert w}_i$ 는 각 기저벡터에 대한 내적으로 만들 수 있다.

\begin{aligned} a^{\Vert w}_i &= (a_i^Tw_1)w_1 + (a_i^Tw_2)w_2 + \cdots + (a_i^Tw_K)w_K \\ \end{aligned} = \sum_{k=1}^K (a_i^Tw_k)w_k

벡터 $a_1, a_2, \cdots, a_N$ 를 행벡터로 가지는 행렬 $A$ 를 가정하면

A = \begin{bmatrix} a_1^T \\ a_2^T \\ \vdots \\ a_N^T \end{bmatrix}

모든 점들과의 거리의 제곱의 합은 다음처럼 행렬의 놈으로 계산할 수 있다.

\begin{aligned} \sum_{i=1}^N \Vert a_i^{\perp w}\Vert^2 &= \sum_{i=1}^N \Vert a_i\Vert^2 - \sum_{i=1}^N \Vert a^{\Vert w}_i\Vert^2 \\ &= \Vert A \Vert^2 - \sum_{i=1}^N \Vert a^{\Vert w}_i\Vert^2 \\ \end{aligned}

행렬 $A$ 는 이미 주어져있으므로 이 값을 가장 작게 하려면 두 번째 항의 값을 가장 크게 하면 된다.
두 번째 항은 K=1일 때와 같은 방법으로 분산행렬 형태로 바꿀 수 있다.

\begin{aligned} \sum_{i=1}^N \Vert a^{\Vert w}_i\Vert^2 &= \sum_{i=1}^N \sum_{k=1}^K \Vert (a_i^Tw_k)w_k \Vert^2 \\ &= \sum_{i=1}^N \sum_{k=1}^K \Vert a_i^Tw_k \Vert^2 \\ &= \sum_{k=1}^K w_k^T A^TA w_k \\ \end{aligned}

분산행렬의 고유분해를 사용하면

\begin{aligned} \sum_{k=1}^K w_k^T A^TA w_k &= \sum_{k=1}^K w_k^T V \Lambda V^T w_k \\ &= \sum_{k=1}^K w_k^T \left( \sum_{i=1}^{M} \sigma^2_iv_iv_i^T \right) w_k \\ &= \sum_{k=1}^K \sum_{i=1}^{M}\sigma^2_i\Vert v_i^Tw_k\Vert^2 \\ \end{aligned}

이 문제도 1차원 근사문제처럼 풀면 다음과 같은 답을 얻을 수 있다.

가장 큰 $K$ 개의 특잇값에 대응하는 오른쪽 특이벡터가 기저벡터일 때 가장 값이 커진다.

11. 랭크-K 근사문제

우리가 찾아야 하는 것은 이 값을 가장 크게 하는 $K$ 개의 영벡터가 아닌 직교하는 단위벡터 $w_k$ 이다. 고유분해의 성질로부터 오른쪽 기저벡터 중 가장 큰 $K$ 개의 특잇값에 대응하는 오른쪽 특이벡터가 우리가 찾는 기저벡터가 된다.

이 문제는 다음처럼 랭크- $K$ 근사문제의 형태로 만들 수도 있다.

\begin{aligned} a^{\Vert w}_i &= (a_i^Tw_1)w_1 + (a_i^Tw_2)w_2 + \cdots + (a_i^Tw_K)w_K \\ &= \begin{bmatrix} w_1 & w_2 & \cdots & w_K \end{bmatrix} \begin{bmatrix} a_i^Tw_1 \\ a_i^Tw_2 \\ \vdots \\ a_i^Tw_K \end{bmatrix} \\ &= \begin{bmatrix} w_1 & w_2 & \cdots & w_K \end{bmatrix} \begin{bmatrix} w_1^T \\ w_2^T \\ \vdots \\ w_K^T \end{bmatrix} a_i \\ &= WW^Ta_i \end{aligned}

이러한 투영벡터를 모아놓은 행렬 $A'$ 는

A'= \begin{bmatrix} \left(a^{\Vert w}_1\right)^T \\ \left(a^{\Vert w}_2\right)^T \\ \vdots \\ \left(a^{\Vert w}_N\right)^T \end{bmatrix} = \begin{bmatrix} a_1^TW^{}W^T \\ a_2^TW^{}W^T\\ \vdots \\ a_N^TW^{}W^T \end{bmatrix} = \begin{bmatrix} a_1^T \\ a_2^T \\ \vdots \\ a_N^T \end{bmatrix} W^{}W^T = AW^{}W^T

따라서 이 문제는 원래 행렬 $A$ 에 랭크-K 행렬 $W_{}W^T$ 를 곱해서 원래의 행렬 $A$ 와 가장 비슷한 행렬 $A'$ 을 만드는 문제와 같다.

\arg\min_{w_1,\cdots,w_K} \Vert A - AW^{}W^T \Vert

※ 출처

김도형의 데이터 사이언스스쿨 중 3.4 특잇값 분해

Jane의 study note.

이전 포스트