좌표와 변환

Jane의 study note.·2022년 10월 10일

선형대수

목록 보기

7/9

이 절에서는 공간상에서 좌표를 정의하기 위해 필요한 개념을 살펴본다. 우선 벡터의 선형독립과 랭크의 개념을 알아보고 기저벡터와 좌표변환이 선형대수와 어떻게 연관이 있는지 공부한다. 좌표변환은 이미지 처리 작업뿐 아니라 다변수 확률변수를 분석하는데도 사용된다.

1. 선형종속과 선형독립

벡터 집합 $x_1, x_2, \ldots, x_N$ 을 이루는 벡터의 선형조합이 영벡터가 되도록 하는 스칼라 계수 $c_1, c_2, \ldots, c_N$ 이 존재하면 이 벡터들이 선형종속(linearly dependent)이라고 한다. 단 $c_1 = c_2 = \cdots = c_N = 0$ 으로 계수가 모두 0인 경우는 제외한다.

c_1 x_1 + c_2 x_2 + \cdots + c_N x_N = 0

반대로 벡터들의 선형조합이 0이 되면서 모두 0은 아닌 계수들이 존재하지 않으면 그 벡터들은 선형독립(linearly independent)이라고 한다.
선형독립을 논리 기호로 나타내면 다음과 같다.

c_1 x_1 + \cdots + c_N x_N = 0 \;\; \rightarrow \;\; c_1 = \cdots = c_N = 0

왼쪽에서 오른쪽 방향 화살표의 의미는 벡터들의 선형조합이 0이면 반드시 계수들이 모두 0이라는 뜻이다.

선형독립을 다음처럼 표현하기도 한다.

c_1 x_1 + \cdots + c_N x_N = 0 \;\; \leftrightarrow \;\; c_1 = \cdots = c_N = 0

오른쪽에서 왼쪽 방향 화살표의 의미는 모든 계수가 0일 때 선형조합이 0이 된다는 뜻이다. 이는 꼭 선형독립이 아니더라도 당연하게 성립한다.

1. 선형독립과 선형 연립방정식

선형독립 관계를 행렬과 벡터의 곱으로 나타낼 수도 있다. 다음 식에서 $c_i$ 는 $x_i$ 에 대한 가중치 계수이고 $c$ 는 $c_i$ 를 원소로 가지는 가중치 벡터이다. $X$ 는 열벡터 $x_1, x_2, \ldots, x_N$ 를 열로 가지는 행렬이다. 이제부터는 벡터의 집합으로 모두 이런 식으로 행렬로 표시하겠다.

c_1 x_1 + \cdots + c_N x_N = \begin{bmatrix} x_1 & x_2 & \cdots & x_N \end{bmatrix} \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_N \end{bmatrix} = X c

따라서 어떤 벡터들이 선형독립인지 아닌지를 알아내는 문제는 선형 연립방정식을 푸는 문제와 같다.

Xc=0

이 연립방정식의 해가 영벡터밖에 없으면 선형독립이다. 만약 영벡터가 아닌 해가 존재하면 선형종속이다. 해가 무한히 많은 경우에는 그 중에 영벡터가 아닌 해가 반드시 존재하므로 선형 종속이다.

벡터 $x_1, x_2, \ldots, x_N$ 이 선형독립이라는 것을 논리기호로 나타내면 다음과 같다.

Xc = 0 \;\; \rightarrow \;\; c=0

$c=0$ 이면 $Xc = 0$ 은 당연히 성립하므로 위 식 대신 다음처럼 쓰기도 한다.

Xc = 0 \;\; \leftrightarrow \;\; c=0

2. 선형종속인 경우

벡터가 선형종속이 되는 대표적인 세 경우를 알아보자. 예측모형을 만들기 위한 특징행렬 $X$ 의 열벡터들이 선형종속이거나 선형종속에 가까운 현상을 다중공선성(multicollinearity)이라고 부른다. 다중공선성이 발생하면 예측의 성능이 나빠지므로 되도록 이러한 경우가 발생하지 않도록 주의해야 한다.

경우 1: 벡터의 개수가 벡터의 차원보다 크면 선형종속이다.

벡터의 차원보다 벡터의 수가 많으면 그 벡터를 행으로 가지는 행렬 $X$ 의 행의 개수보다 열의 개수가 많다. 따라서 이 행렬이 표현하는 연립방정식을 고려하면 미지수의 수가 방정식의 수보다 커서 해가 무한히 많다. 해가 무한히 많다는 것은 영벡터가 아닌 해 $c$ 도 존재한다는 뜻이다. 따라서 그 벡터들은 선형종속이다.
반대로 행의 개수가 열의 개수와 같거나 크면 대부분 선형독립이다. 우리가 분석할 대부분의 데이터는 데이터(행)의 수가 특징(열)의 수보다 많기 때문에 여기에 해당한다.

경우 2: 값이 같은 벡터가 있으면 반드시 선형종속이다.

만약 $i$ 번째 벡터 $x_j$ 와 $j$ 번째 벡터 $x_j$ 가 같으면 $c_j = -c_i$ 로 놓고 다른 $c$ 값은 모두 0으로 하면

\begin{aligned} & 0 \cdot x_1 + \cdots + c_i \cdot x_i +\cdots + c_j \cdot x_j + \cdots + 0 \cdot x_N \\ &= 0 \cdot x_1 + \cdots + c_i \cdot x_i +\cdots + (-c_i) \cdot x_j + \cdots + 0 \cdot x_N \\ &= 0 \end{aligned}

따라서 다음처럼 중복된 데이터가 있으면 선형종속이다.

\begin{bmatrix} 1 & 5 & 1 \\ 3 & 6 & 3 \\ 4 & 6 & 4 \end{bmatrix}

벡터 $x_j$ 가 벡터 $x_i$ 의 실수배인 경우도 마찬가지이다.

예측 모형을 위한 특징행렬을 만들 때 실수로 위와 같은 행렬을 만드는 경우가 종종 있다. 우리가 실무에서 다루게 되는 데이터는 그 양이 크기 때문에 엑셀 등으로 한 눈에 볼 수 없는 경우가 많아서 위와 같은 실수를 하는 경우에도 빨리 발견하기 어렵다.

경우 3: 어떤 벡터가 다른 벡터의 선형조합이면 반드시 선형종속이다.

예를 들어 벡터 $x_1$ 과 다른 벡터 $x_2, x_3$ 사이에 다음 관계가 성립한다고 하자.

x_1 = 2 x_2 - 3 x_3

그러면 $c_1=-1, c_2=2 c_3=-3$ 일 때

-1\cdot x_1 + 2 x_2 - 3 x_3 = 0

이므로 선형종속이다.

이 경우도 데이터 분석에서 흔히 하는 실수이다. 예를 들어 국어, 영어, 수학 점수를 각각 별도의 데이터로 포함하면서 이 세 점수에 의존하는 총점수나 평균을 다시 데이터로 포함하면 선형종속이 된다.

2. 랭크

행렬의 열벡터 중 서로 독립인 열벡터의 최대 개수를 열랭크(column rank)라고 하고
행벡터 중 서로 독립인 행벡터의 최대 개수를 행랭크(row rank)라고 한다.
행랭크와 열랭크에 대해서는 다음 정리가 성립한다.

[정리] 행랭크와 열랭크는 항상 같다.

따라서 행 랭크나 열 랭크를 그냥 랭크(rank)라고 하기도 한다.
행렬 $A$ 의 랭크는 기호로 $\text{rank}A$ 와 같이 표시한다.

행랭크는 행의 개수보다 커질 수 없고 열랭크는 열의 개수보다 커질 수 없기 때문에 행의 개수가 $N$ 이고 열의 갯수가 $M$ 인 행렬의 랭크는 행의 개수 $N$ 과 열의 개수 $M$ 중 작은 값보다 커질 수 없다.

\text{rank} A \leq \min(M, N)

A \in \mathbf{R}^{N \times M}

넘파이 linalg 서브 패키지의 `matrix_rank()` 함수로 행렬의 랭크를 계산할 수 있다.

X1 = np.array([[1, 3], [2, 4]])
np.linalg.matrix_rank(X1)

1. 풀랭크

위에서 예로 든 행렬 $X_1$ 나 $X_2$ 처럼 랭크가 행의 개수와 열의 개수 중 작은 값과 같으면 풀랭크(full rank)라고 한다.

\text{rank}A = \min(M, N)

선형독립인 벡터들을 행 또는 열로 가지는 행렬을 만들면 정의에 의해 항상 풀랭크다.

2. 로우 랭크 행렬

$N$ 차원 벡터 $x$ 하나를 이용하여 만들어지는 다음과 같은 행렬을 랭크-1 행렬(rank-1 matrix)이라고 한다.

xx^T \in \mathbf{R}^{N \times N}

이 행렬의 열벡터들은 $x$ 라고 하는 하나의 벡터를 $x_1$ 배, $x_2$ 배, ... $x_n$ 배한 벡터이므로 독립적인 열벡터는 1개다. 따라서 랭크-1 행렬의 랭크는 1이다.

\begin{aligned} xx^T &= x \begin{bmatrix} x_1 & x_2 & \cdots & x_n \end{bmatrix} \\ &= \begin{bmatrix} x_1x & x_2x & \cdots & x_nx \end{bmatrix} \end{aligned}

선형독립인 두 개의 $N$ 차원 벡터 $x_1, x_2$ 를 이용하여 만든 다음과 같은 행렬은 랭크-2 행렬(rank-2 matrix)이라고 한다.

\begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} x_1^T \\ x_2^T \end{bmatrix} = x_1x_1^T + x_2x_2^T

앞서와 비슷한 방법으로 랭크-2 행렬의 랭크는 2임을 보일 수 있다.

만약 $M$ 개의 $N$ 차원 벡터 $x_1, x_2, \cdots, x_M$ 을 이용하면 랭크-M 행렬(rank-M matrix)이 된다.

\begin{bmatrix} x_1 & x_2 & \cdots & x_M \end{bmatrix} \begin{bmatrix} x_1^T \\ x_2^T \\ \vdots \\ x_M^T \end{bmatrix} = x_1x_1^T + x_2x_2^T + \cdots + x_Mx_M^T = \sum_{i=1}^M x_ix_i^T

이러한 행렬들을 가리켜 로우-랭크 행렬(low-rank matrix)이라고 한다. 로우-랭크 행렬은 나중에 특이분해(singular value decomposition)와 PCA(principal component analysis)에서 사용된다.

3. 벡터공간과 기저벡터

여러 벡터를 선형조합을 하면 다른 벡터를 만들 수 있다. 벡터 N개가 서로 선형독립이면 이 벡터들을 선형조합하여 만들어지는 모든 벡터의 집합을 벡터공간(vector space) $V$ 라 하고 이 벡터공간의 차원을 $N$ 이라고 한다. 그리고 그 벡터들을 벡터공간의 기저벡터(basis vector)라고 한다.

V = \{ c_1x_1 + \cdots + c_Nx_N \; \vert \; c_1, \ldots, c_N \in \mathbf{R} \}

벡터공간의 차원(dimension)이 벡터의 차원(길이)가 아니라 기저벡터의 개수로 정의된다는 점에 유의해야 한다.

$N$ 차원 벡터 $N$ 개 $x_1, x_2, \cdots, x_N$ 이 선형독립인 경우에는 다음 정리가 성립한다.

[정리] $N$ 개의 $N$ 차원 벡터 $x_1, x_2, \cdots, x_N$ 이 선형독립이면 이를 선형조합하여 모든 $N$ 차원 벡터를 만들 수 있다.

다음과 같이 증명한다. 임의의 벡터 $x$ 가 있다고 하자. 기저벡터 $x_1, x_2, \cdots, x_N$ 와 이 벡터 $x$ 를 열벡터로 사용하여 만든 행렬

X = \left[ x_1, x_2, \cdots, x_N, x \right]

는 크기가 $N \times (N+1)$ 이므로 랭크값은 $N$ 보다 커질 수는 없다. 그런데 $N$ 개의 선형독립인 열벡터가 있기 때문에 랭크값은 $N$ 이고 풀랭크다. 따라서 어떠한 $N$ 차원 벡터를 생각하더라도 기저벡터의 조합으로 표현할 수 있다.

1. 랭크와 역행렬

정방행렬의 랭크와 역행렬 사이에는 다음과 같은 정리가 성립한다.

[정리] 정방행렬이 풀랭크면 역행렬이 존재한다. 역도 성립한다. 즉, 정방행렬의 역행렬이 존재하면 풀랭크다.

따라서 다음 두 문장은 같은 뜻이다.

정방행렬이 풀랭크다 $\leftrightarrow$ 역행렬이 존재한다

다음과 같이 증명한다.

(1)
우선 왼쪽에서 오른쪽 방향 즉, 정방행렬이 풀랭크이면 역행렬이 존재한다는 것을 증명하자. 정방행렬이 풀랭크이면 선형독립이고 기저벡터가 되므로 어떠한 벡터에 대해서도 그 벡터를 만들 수 있는 선형조합을 생각할 수 있다. 예를 들어 다음과 같은 벡터 $e_1, \cdots, e_N$ 을 만들기 위한 조합 $c_1, \cdots, c_N$ 도 있을 수 있다.

Xc_1 = e_1 = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}

Xc_2 = e_2 = \begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix}

이 식들을 모으면 다음과 같아진다.

X \begin{bmatrix} c_1 & c_2 & \cdots & c_N \end{bmatrix} = XC = I

정방행렬의 경우 $XC=I$ 이면 $CX=I$ 가 성립한다.(연습문제 2.4.4) 따라서

XC = CX = I

인 행렬 $C$ 가 존재한다. 이 행렬이 역행렬이다.

(2)
다음으로 오른쪽에서 왼쪽 방향 즉, 역행렬이 존재하면 풀랭크라는 것을 증명하자.
역행렬이 존재하는 경우에 다음 식이 성립한다는 것을 증명하면 된다.

Xc = 0 \;\; \leftrightarrow \;\; c=0

(i) 우선 역행렬이 존재하든 말든 $c = 0$ 이면 $Xc=0$ 는 당연하다. 따라서 오른쪽에서 왼쪽 방향은 증명된다.

(ii) 다음으로 역행렬이 존재할 때 $Xc=0$ 이면

X^{-1}Xc = c = 0

이므로 왼쪽에서 오른쪽 방향도 증명된다. 따라서 역행렬이 존재하면 풀랭크다.

4. 투영

벡터공간 투영

$M$ 개의 $N$ 차원 기저벡터 $v_1, v_2, \cdots, v_M$ 가 존재한다고 하자. $M$ 은 $N$ 보다 작다.
이 때 모든 $N$ 차원 벡터 $x$ 에 대해 기저벡터 $v_1, v_2, \cdots, v_M$ 를 선형조합하여 만든 벡터 $x^{\Vert v}$ 와 원래 벡터 $x$ 의 차 $x - x^{\Vert v}$ 가 모든 기저벡터에 직교하면 그 벡터 $x^{\Vert v}$ 를 $v_1, v_2, \cdots, v_M$ 벡터공간에 대한 투영벡터라 하고 차이 벡터 $x - x^{\Vert v} = x^{\perp v}$ 를 벡터공간에 대한 직교벡터라 한다.

(x - x^{\Vert V}) \perp \{ v_1, v_2, \cdots, v_M \}

다음 그림은 $N=3,M=2$ 즉 3차원 벡터를 2차원 벡터공간에 투영하는 예를 보인 것이다.

정규직교인 기저벡터로 이루어진 벡터공간

만약 기저벡터 $v_1, v_2, \cdots, v_M$ 가 정규직교(orthonormal)이면 투영벡터 $x^{\Vert v}$ 는 각 기저벡터에 대한 내적값으로 표현된다.

x^{\Vert V} = (x^Tv_1)v_1 + (x^Tv_2)v_2 + \cdots + (x^Tv_M)v_M

그리고 투영벡터의 길이의 제곱은 각 기저벡터와의 내적의 제곱합이다.

\Vert x^{\Vert V} \Vert^2 = \sum_{i=1}^M (x^Tv_i)^2

벡터 $x$ 에서 이 벡터 $x^{\Vert V}$ 를 뺀 벡터 $x - x^{\Vert V}$ , 즉 직교벡터 $x^{\perp V}$ 가 기저벡터 $v_1, v_2, \cdots, v_M$ 에 모두 직교한다는 것은 다음처럼 증명할 수 있다.

\begin{aligned} v_i^T(x - x^{\Vert v}) &= v_i^Tx - v_i^T \left( (x^Tv_1)v_1 + (x^Tv_2)v_2 + \cdots + (x^Tv_M)v_M \right) \\ &= v_i^Tx - \left( (x^Tv_1)v_i^Tv_1 + (x^Tv_2)v_i^Tv_2 + \cdots + (x^Tv_M)v_i^Tv_M \right) \\ &= v_i^Tx - x^Tv_i \\ &= 0 \end{aligned}

따라서 직교벡터 $x^{\perp V}$ 는 기저벡터 $v_1, v_2, \cdots, v_M$ 으로 이루어진 벡터공간의 모든 벡터에 대해 직교한다.

이 사실로부터 벡터 $x$ 의 투영벡터 $x^{\Vert V}$ 은 기저벡터 $v_1, v_2, \cdots, v_M$ 으로 이루어진 벡터공간의 모든 벡터 중에서 가장 벡터 $x$ 와 가까운 벡터라는 것도 알 수 있다.

기저벡터 $v_1, v_2, \cdots, v_M$ 으로 이루어진 벡터공간의 어떤 벡터를 $y$ 라고 하자. 그러면 $x^{\Vert V}$ 와 $y$ 의 차이 벡터 $x^{\Vert v} - y$ 도 $v_1, v_2, \cdots, v_M$ 으로 이루어진 벡터공간에 존재하므로 직교벡터 $x^{\perp V}$ 와 직교한다.

\begin{aligned} \Vert x - y \Vert^2 &= \Vert x - x^{\Vert V} + (x^{\Vert V} - y) \Vert^2 \\ &= \Vert x^{\perp V} + (x^{\Vert V} - y) \Vert^2 \\ &= \Vert x^{\perp V} \Vert^2 + \Vert (x^{\Vert V} - y) \Vert^2 \\ &\geq \Vert x^{\perp V} \Vert^2 \end{aligned}

5. 표준기저벡터

기저벡터 중에서도 원소 중 하나만 값이 1이고 다른 값은 0으로 이루어진 다음과 같은 기저벡터를 표준기저벡터(standard basis vector)라고 한다.

e_1 = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}, \;\; e_2 = \begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix}, \;\; \cdots, \;\; e_N = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix}

표준기저벡터를 열로 가지는 행렬은 항등행렬이 된다.

\begin{bmatrix} e_1 & e_2 & \cdots & e_N \end{bmatrix} = I_N

6. 좌표

어떤 벡터의 좌표(coordinate)는 기저벡터를 선형조합하여 그 벡터를 나타내기 위한 계수벡터를 말한다.

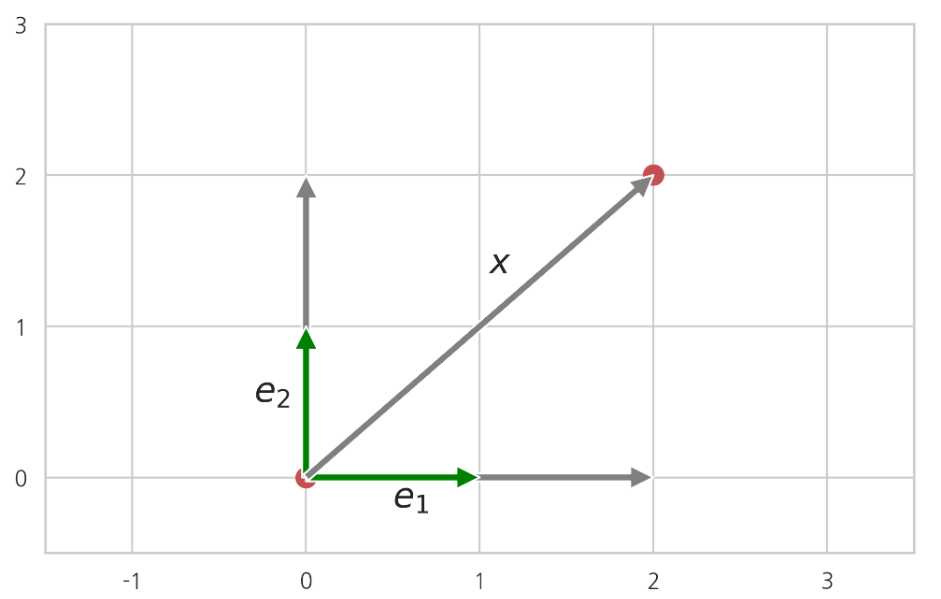
예를 들어 다음처럼 기저벡터 $\{e_1,e_2\}$ 를 선형조합하여 벡터 $x$ 를 나타낼 수 있다고 가정하자.

x = x_{e_1} e_1 + x_{e_2} e_2

이 때 벡터 $x_e$

x_e = \begin{bmatrix} x_{e_1} \\ x_{e_2} \end{bmatrix}

를 벡터 $x$ 의 기저벡터 $\{e_1,e_2\}$ 에 대한 좌표벡터 혹은 간단히 좌표(coordinate)라고 한다. 벡터와 기저벡터 그리고 좌표의 관계는 다음과 같다.

x = [ e_1 e_2 ] \begin{bmatrix} x_{e_1} \\ x_{e_2} \end{bmatrix} = [ e_1 e_2 ] \; x_e

표준기저벡터를 모아놓은 행렬이 항등행렬이기 때문에 표준기저벡터에 대한 벡터의 좌표 $x_e$ 는 원래 벡터 $x$ 와 같다. 하지만 같은 벡터라도 다른 기저벡터를 사용하면 좌표가 달라진다. 따라서 하나의 벡터도 기저벡터에 따라 여러 좌표를 가질 수 있다.

※ 출처

김도형의 데이터 사이언스스쿨 중 3.2 좌표와 변환

Jane의 study note.

이전 포스트

선형대수와 해석기하의 기초

다음 포스트