키워드: 차원축소, 선형결합(linear combination), 공분산 행렬(covariance matrix), 상관계수(correlation), 피어슨 상관계수, 공분산(covariance), 사영(Projection)

주성분 분석 ( PCA : Principal Component Analysis )

참고자료

1. 김성범 소장, [핵심 머신러닝] 중 주성분분석(PCA) 강의
2. 주재걸, 인공지능을 위한 선형대수
3. 파이썬 라이브러리를 활용한 머신러닝
4. 핸즈온 머신러닝, 박해선 강의
5. 이어드림, 김용담, 이상엽 강의

1. 주성분 분석 개요

1) 주성분 분석이 등장하게 된 배경과 차원축소

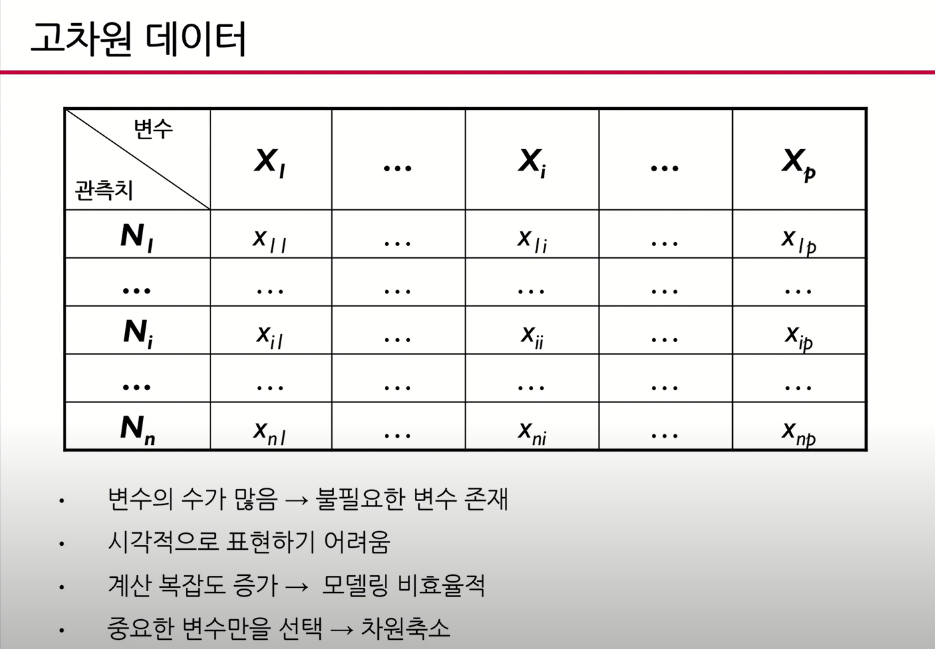
• 고차원 데이터는 X변수의 수가 굉장히 많은 데이터를 말함 -> 제조업, 의류업체에서 고성능의 데이터 수집기기의 등장으로 고차원 데이터가 도출되서 생산되고 있음
• 고성능 데이터를 수집하는 사람들은 데이터 분석을 목적으로 하고 있지 않기 때문에 데이터가 많아서 좋기도 하지만불필요한 변수도 존재하기도 함
• 고차원 데이터는 시각적으로 표현하기가 어려움
• 데이터의 양이 많아서 데이터의 계산복잡도가 증가해서 모델이 비효율적인 경우도 있음
• 이 경우 중요한 변수만 선택하는 방법이 많이 사용되는데 이를 차원축소라고 한다.

2) 차원을 축소하는 방법 2가지: 변수 선택, 변수 추출

• 변수선택(selection): 분석 목적에 부합하는 소수의 예측변수만을 선택
  - 장점: 오리지널 원래 변수를 그냥 뽑는 것이기 때문에 해석이 용이함
  - 단점: 다변량 데이터에서는 상관관계가 존재하는데 이를 고려하지 못함
• 변수추출(extraction): 그냥 뽑는 것이 아니라예측 변수(기존 변수)의 변환을 통해 새로운 변수 추출
  - 새로운 변수 $z$를 정의하고 이는 기존 변수들의 변환을 통해 추출된 값
  - $z = f(x_1, x_2, ... x_{100})$
  -단점: 추출된 새로운 z변수는 원래변수의 결합으로 되어있기 때문에 해석이 용이하지 않음

3) 변수선택/추출을 통한 차원 축소

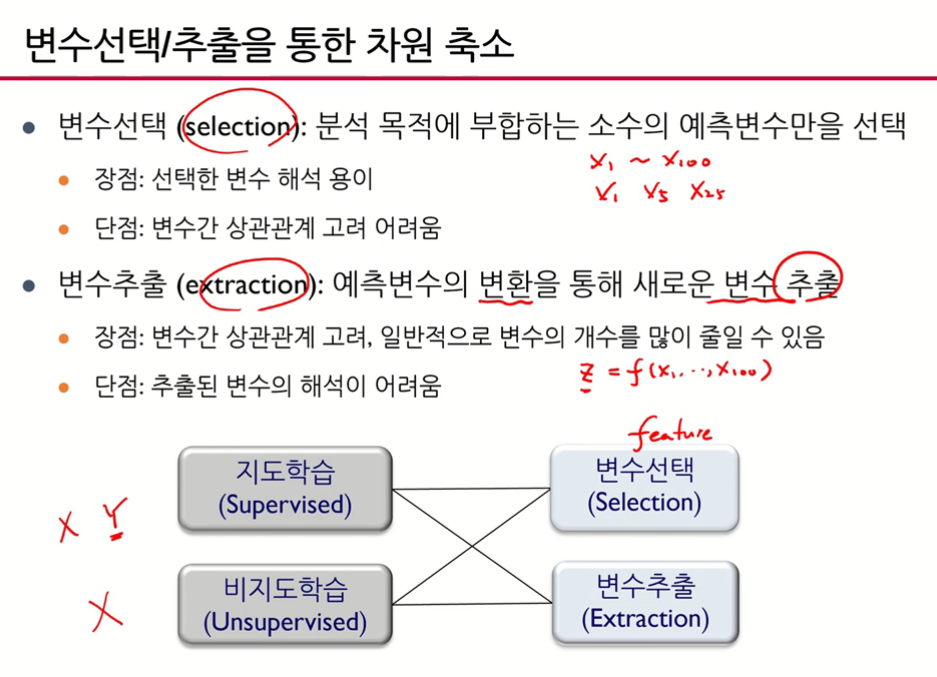
• 지도 변수 선택볍
• 지도 변수 추출볍
• 비지도 변수 선택볍 :
• 비지도 변수 추출볍 : y를 이용하지 않고 x들의 결합으로 변수 추출 -> PCA

4) 주성분 분석 스펠링

5) 주성분 분석 개요

• 차원을 축소한다 = 중요한 변수를 추출한다.
• 차원을 축소하면 시각화, 군집화, 압축이 가능하다.

최근에 우리가 볼 수 있는 데이터 대부분이 고차원 데이터이다.

• 고차원 데이터는 많다. 예를 들어, 이미지는 여러 개의 픽셀로 구성되고 픽셀 하나하나가 변수가 되는 고차원 데이터이고 고해상도의 이미지는 X변수가 굉장히 많다.
• 오른쪽 위그림처럼 시그널(신호)도 선들의 연속이 무수히 많은 점들의 연속으로 구성되는데 점하나하나가 X변수가 되는 굉장히 고차원 데이터이다.
• 그 외 네트워크 데이터(오른쪽 그림 아래)나 텍스트 데이터도 고차원 데이터이다.
• 최근에 우리가 볼 수 있는 데이터 대부분이 고차원 데이터이다.

• 데이터의 변수가 너무 많아서 효율성이 떨어질 때 줄이는 변수로 모델링을 하는 용도로 많이 사용한다.
  
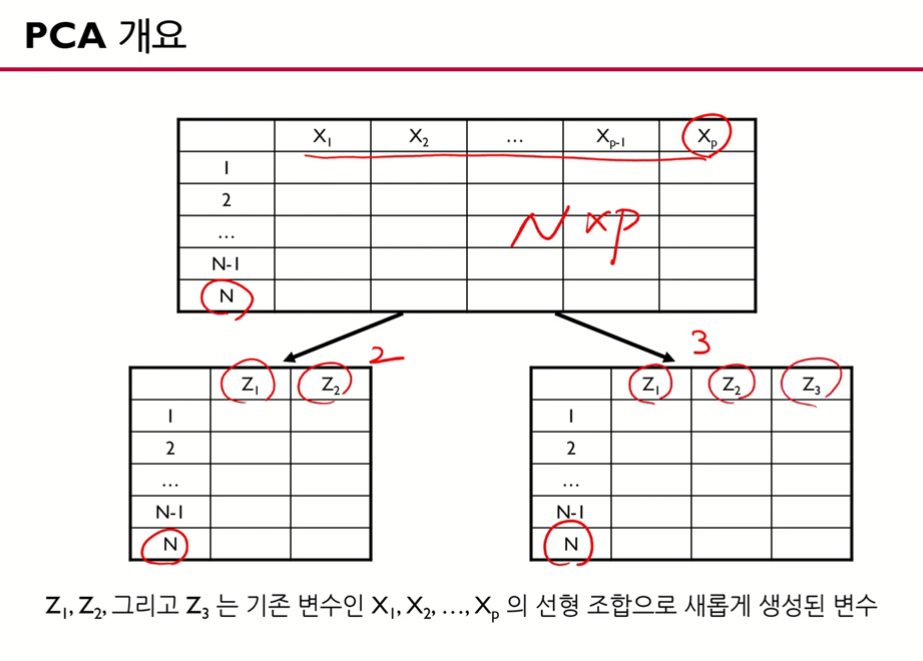
• 변수의 수를 2개로 3개로 줄임
  
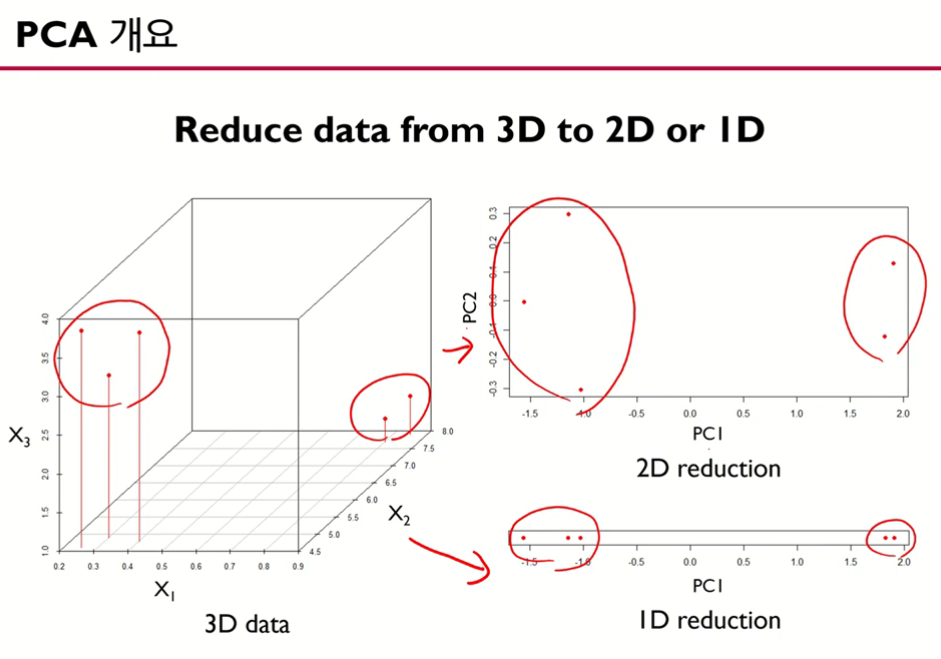
• 원래 데이터가 3차원에서 주성분 분석을 통해 2차원, 1차원으로 줄임
• 원래 데이터 관측치가 3+2=5개가 있음
• 차원을 축소했음에도 2차원, 1차원에도 관측치가 모두 5개씩 있음(데이터가 잘 보존됨)

• $Z$는 모든 $X$변수★를 가지고 선형결합을 함
• 선형 결합(linear combination)이란 $X$들의 더하기와 빼기로만 결합을 시킨 결합을 의미함
• $Z_1$,$Z_2$,$Z_p$.. 모두 X들의 선형결합
• $Z_1$,$Z_2$,$Z_p$이 뭐가 다른가? -> X는 같은데 앞에 있는 계수들,$\alpha$가 다 다름, 그래서 $Z_1$,$Z_2$는 다른 변수
• 원래 변수 $X$도 $p$개가 있고 새로운 변수 $Z$도 $p$개가 있다. (똑같은 갯수의 추출된 변수들을 얻을 수 있다.)
• $Z$가 핵심, 주성분(주가 되는 성분들을 추출했다)

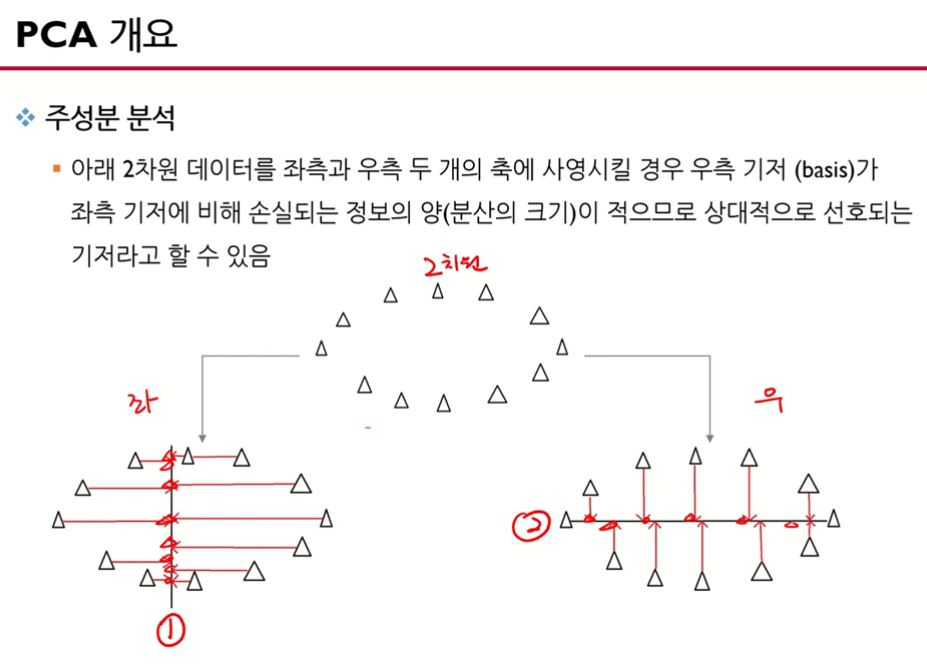
• X변수들을 가지고 Z(주성분)을 찾아야 함
• 그림은 2차원의 데이터를 1차원으로 바꾸려고 하는 것
  - 좌측은 세로선(1번축)에 데이터 세모를 사영(projection) 시킴
  - 우측은 가로선(2번축)에 데이터 세모를 사영(projection) 시킴
  - 사영 후에 데이터의 분산을 보면 1번이 클까? 2번이 클까? 2번이 분산이 더 크다.
  - 자세한 이유는 다음 그림 참고
  
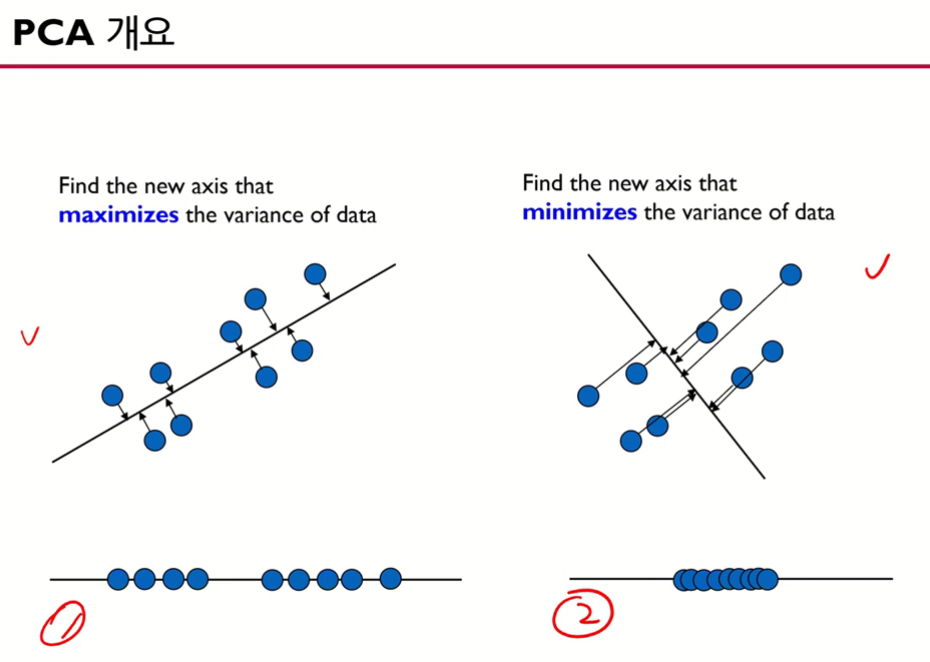
• 이 그림에서는 1번의 분산이 크다.
• 주성분 분석 관점에서는 1번이 좋다. 즉, 분산이 큰 것이 주성분 분석에서는 좋다!
• 이처럼 원래 데이터의 분산을 최대로 하는 축을 찾겠다는 것

2. 주성분 분석 수리적 배경

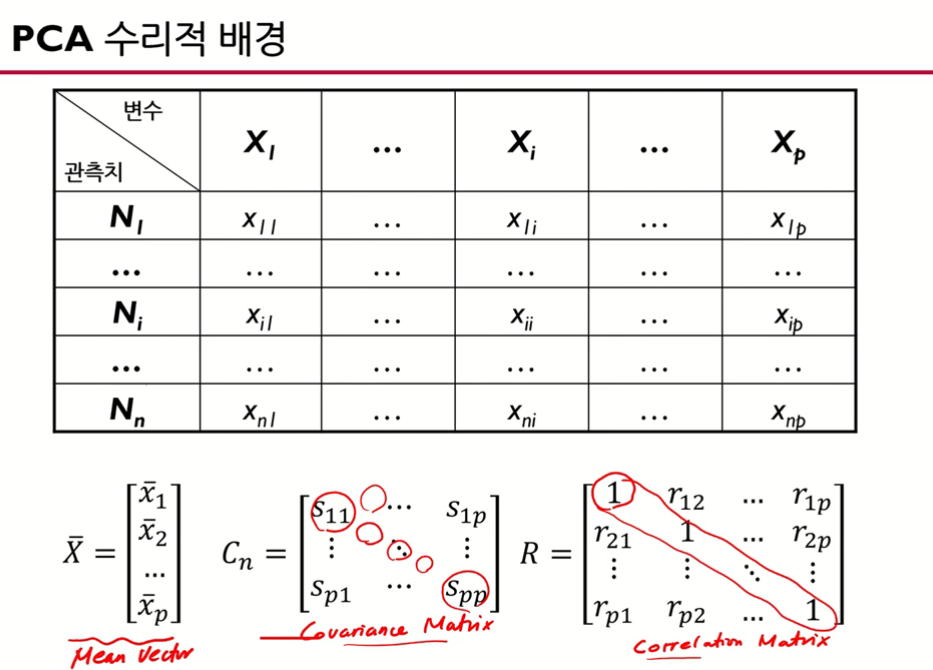
• $X$가 $p$개인 고차원의 다변량 데이터
• 고차원 데이터($x$가 $p$개인 다변량 데이터)를 요약하는 matrix measure는 여러 개가 있다.
  - 1) mean vector: 평균을 담고 있는 벡터
  - 2) covariance matrix (공분산 행렬)
  - 3) correlation matrix (상관계수 행렬): 공분산을 분산들을 곱해서 제곱근을 취한 값으로 나눠주면 (피어슨 상관계수식) 상관계수(correlation)를 얻을 수 있음, 행렬에 상관계수가 들어가 있음, 대각에 있는 원소는 자기자신과의 상관관계이기 때문에 1이 들어감.
  -> 2), 3)은 우리가 가지고 있는 고차원 데이터의 상관계수, 상관관계에 대한 정보를 잘 요약하고 있는 행렬, 굉장히 중요한 정보들이다.
  
• 대각원소에는 각 변수의 분산이 담겨져 있고 비대각원소에는 2개의 변수의 공분산이 들어가 있다.

사영 (projection)

20:18~

3. 주성분 분석 알고리즘

4. 주성분 분석 예제

---

주성분 분석

• 가장 인기 있는 차원 축소 알고리즘
• 데이터에 가장 가까운 초평면을 해석적으로 정의한 후, 그 평면에 데이터를 투영시키는 방법

분산 보존

• PCA는 훈련 세트에서 분산이 최대인 축을 찾음
1. 위 그림에서는 실선
2. 또한 첫 번째 축에 직교하고(수직이고) 남은 분산을 최대로 보존하는 두 번째 축을 찾음
• 2D 예제에서는 직교인 축이 1개밖에 없으므로 선택의 여지가 없음 => 점선이 됨
3. 고차원 데이터셋이라면 PCA는 이전의 두 축에 직교하는 세 번째 축을 찾음
4. 데이터 셋에 있는 차원의 수만큼 n번째 축을 찾음
• i번째 축을 이 데이터의 i번째 주성분(PC : Principal Component)이라고 부름
• 즉, 첫번째 PC는 벡터 𝑐! 이 놓인 축
• 두 번째 PC는 벡터 𝑐" 가 놓인 축

주성분

주성분 주의할 점

특잇값 분해 ( SVD: Singular Value Decomposition )

• 훈련 데이터 셋의 주성분을 찾는 방법
• 표준 행렬 분해 기술로, 훈련 세트 행렬 X를 세 개 행렬의 행렬 곱셈인 𝑈Σ𝑉! 로 분해할 수 있음
• 여기서 찾고자 하는 모든 주성분의 단위 벡터가 V에 다음과 같이 담겨 있음

d차원으로 투영하는 방법 ( 유사역행렬 기반 )

사이킷런으로 PCA 이용하기

설명된 분산의 비율 ( 설명력 )

적절한 차원 수 선택하는 방법 ( MNIST 784차원 데이터 기반 )

PCA에서 적절한 차원 수 선택하는 방법

PCA 기반 압축화 기능 ( 압축 )

PCA 기반 압축화 기능 ( 재복원 )

랜덤 PCA

점진적 PCA

커널 트릭

샘플을 매우 높은 고차원 공간으로 암묵적으로 매핑하여,
서포트 벡터 머신의 비선형 분류와 회귀를 가능하게 하는 수학적 기법
• 고차원 특성 공간에서의 선형 결정 경계는 원본 공간에서는 복잡한 비선형 결정 경계에 해당함

커널 PCA

같은 기법을 PCA에 적용해 차원 축소를 위한 복잡한 비선형 투영 수행 가능
• 투영된 후 샘플의 군집을 유지하거나 꼬인 매니폴드에 가까운 데이터 셋을 펼칠 때도 유용하다

커널 PCA 활용 해보기 ( 스위스 롤 데이터 )

사이킷런 KernelPCA를 이용 ( Kernel=‘rbf’ )

커널 선택과 하이퍼파라미터 튜닝

---

지역선형임베딩 ( LLE : Locally Linear Embedding )

또 다른 강력한 비선형 차원 축소(NLDR) 기술
• 이전 알고리즘처럼 투영에 의존하지 않는 매니폴드 학습
• LLE는 각 훈련 샘플이 가장 가까운 이웃에 얼마나 선형적으로 연관되어 있는지 측정
• 그 후 국부적인 관계가 가장 잘 보존되는 훈련 세트의 저차원 표현을 찾게 됨
• 잡음이 너무 많지 않은 경우 꼬인 매니폴드를 펼치는데 잘 작동하는 방법이다

LLE 활용 해보기 ( 스위스 롤 데이터 )

다른 차원 축소 기법

1. 랜덤 투영

랜덤한 선형 투영을 사용해 데이터를 저차원 공간으로 투영
• 이러한 랜덤 투영이 실제로 거리를 잘 보존함
• 차원 축소 품질은 샘플 수와 목표 차원수에 따라 다르며, 초기 차원수에는 의존적이지 않음

2. 다차원 스케일링(MDS)

샘플 간의 거리를 보존하면서 차원을 축소

3. Isomap

각 샘플을 가장 가까운 이웃과 연결하는 식으로 그래프를 만드는 방법
• 그 후 샘플 간의 지오데식 거리를 유지하면서 차원을 축소

4. t-SNE

비슷한 샘플은 가까이, 비슷하지 않은 샘플은 멀리 떨어지도록 하면서 차원을 축소

5. 선형 판별 분석(LDA)