랜덤 포레스트 (Random Forest)

참고자료

1. 김성범 소장, [핵심 머신러닝] 중 의사결정나무모델 강의
2. 파이썬 라이브러리를 활용한 머신러닝
3. 핸즈온 머신러닝, 박해선 강의
4. 이어드림, 김용담, 이상엽 강의

0. 앙상블 (ensemble)

• 랜덤 포레스트의 배경
• 여러 base 모델들의 예측을 다수결 법칙 또는 평균을 이요해 통합하여 예측 정확성을 향상시키는 방법
• 분류문제에서 무작위 예측을 한다는 것은 0.5
  - 2가지 경우 밖에 없으므로 대충해도 0.5는 나옴
  
  
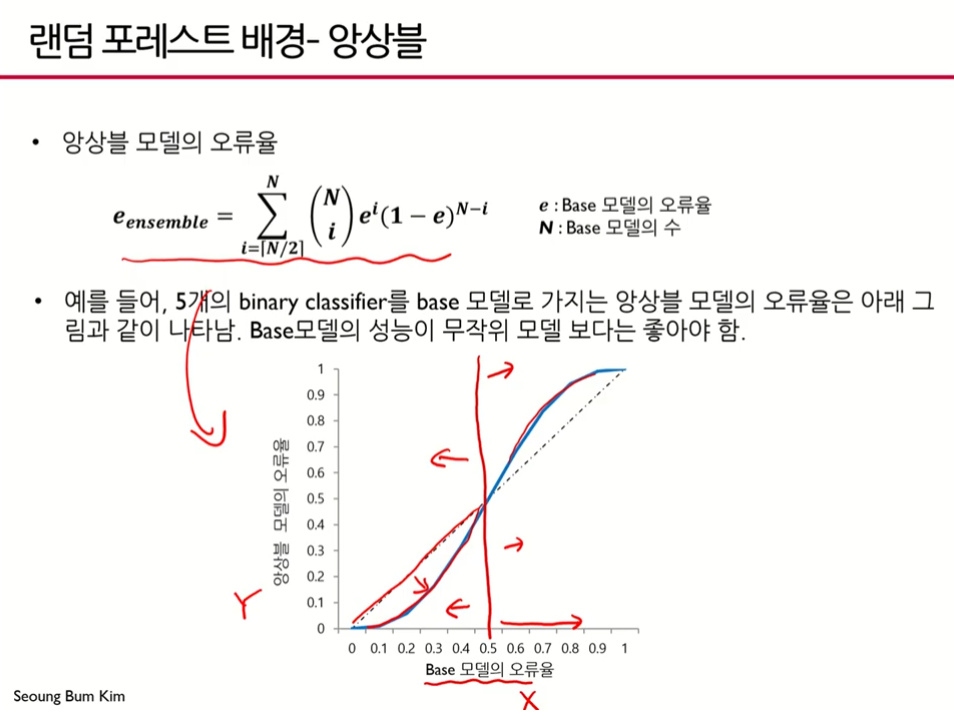
• 베이스모델의 오류율이 안좋은 경우(x축, 0.5보다 큰 경우) 앙상블 모델의 오류율(y축)도 더 커진다. 베이스모델이 오류율이 커질수록 앙상블 모델은 더욱 커진다. 베이스모델을 1개 사용했을 때보다 오히려 안좋다.
• 그러나 베이스 모델의 오류율이 0.5보다 작은 경우에 이를 앙상블할 경우에 오류율이
  그래프와 같이 훨씬 더 줄어들 수 있다.
  
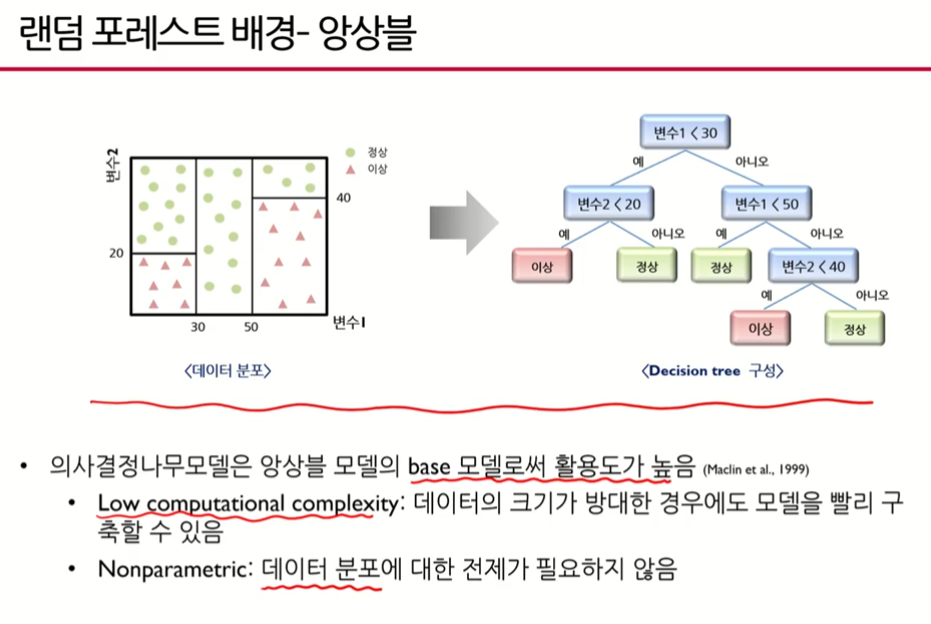
  랜덤포레스트가 앙상블 모델의 베이스 모델로서 사용되는 이유
• 빠른 연산량
• 데이터의 분포가 필요하지 않음, 정규분포를 따라야 한다든지, 지수분포를 따라야 한다는지와 같은 전제가 필요하지 않다. 넌파라메트릭, 비모수적 모델

1. 랜덤포레스트

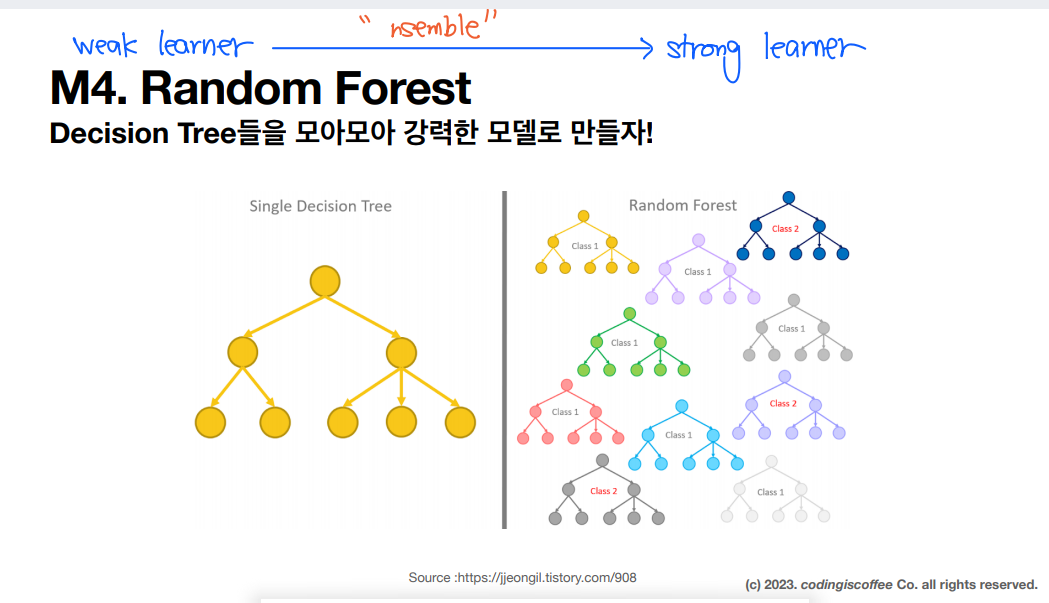
• 배깅
• 랜덤 서브스페이스
• 2번: 개별모델의 독립성을 확보하기 위해 변수를 무작위로 선택함

1) 배깅 (Bagging, Bootstrap Aggregating)

• Bootstrap : 샘플링, 한 번 시작되면 알아서 진행되는 일련의 과정
• Aggregating : 집계
  
  z
• 배깅(Bagging)은 Bootstrap Aggregating의 약자로, 중복을 허용한 랜덤 샘플링을 통해 여러 개의 모델을 학습하고, 이들의 예측을 평균 또는 다수결 방식으로 결합하여 최종 예측을 수행하는 앙상블 학습 방법이다.
  
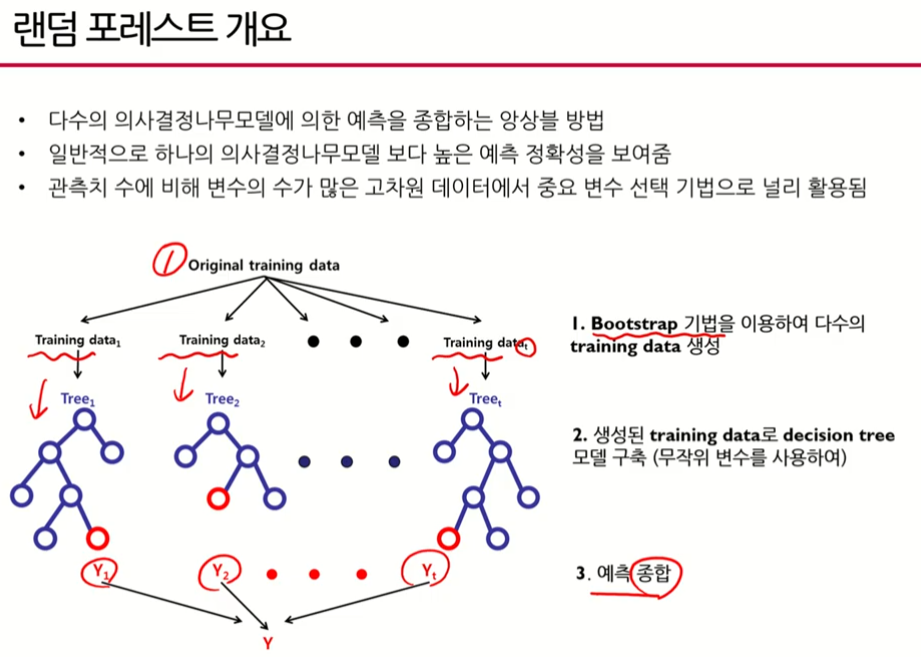
• 원래 데이터(observations)가 있고 부트스트랩을 통해 여러개의 학습데이터를 획득한 후(여기서는 M개) 각각의 학습 데이터에 대해 의사결정나무모델을 만들고 그 결과들을 통해서 우리가 최종적으로 예측(Forest)한다.
  
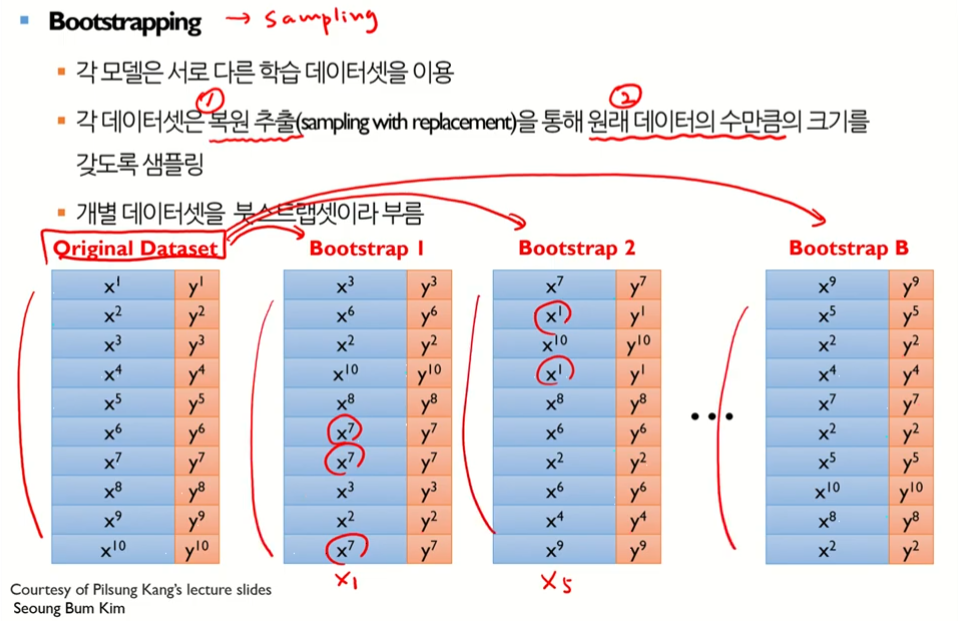
• 부트스트랩 샘플링은 1) 복원추출이어야 하고 2) 원래 데이터의 수만큼 크기를 가져야 한다.
  - 위 그림처럼 복원추출이기 때문에 하나의 데이터가 $x^7$처럼 여러 번 선택 될수도 있고 아예 추출되지 않을 수도 있다.
  - 또한 원본 데이터가 10개 있었기 떄문에 부트스트랩(샘플링) 시행 시 10개를 뽑아야 한다.
  
• 한번도 선택되지 않을 확률은 이론상 0.368이다. (※계산: 수악중독 자연상수 $e$)
• 배깅에서 각 모델이 선택될 확률은 $(1 - \frac{1}{n})$이다. 이는 하나의 데이터 샘플이 선택되지 않을 확률이기도 하다.
• n개의 모델이 모두 독립적으로 선택되지 않을 확률은 $(1 - \frac{1}{n})^n$이다.
  
• 1방법: 다수결 원칙에 의한 방법
• 학습 정확도
• Ensemble population 부스트랩스 셋(의사결정나무모델) 10개를 생성
• test instance(observations)에 대해 y가 1일 확률, 0.5보다 크면 레이블이 1로 예측, 작으면 0으로 예측됨
• 예측된 레이블
  
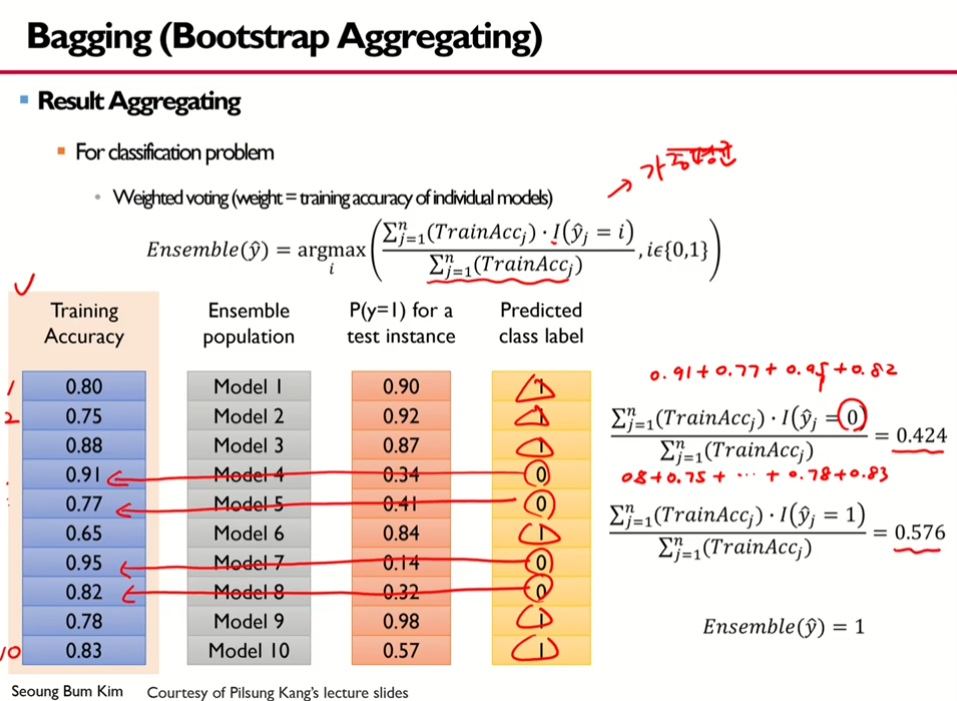
• 2방법: 가중평균에 의한 방법
  
  

2) 랜덤 서브스페이스 (Random Subspace)

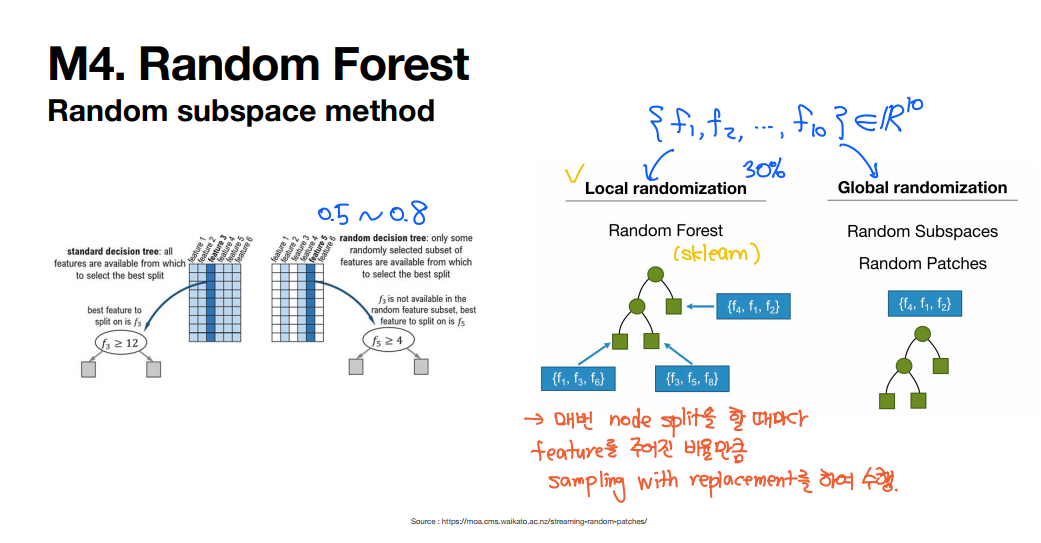
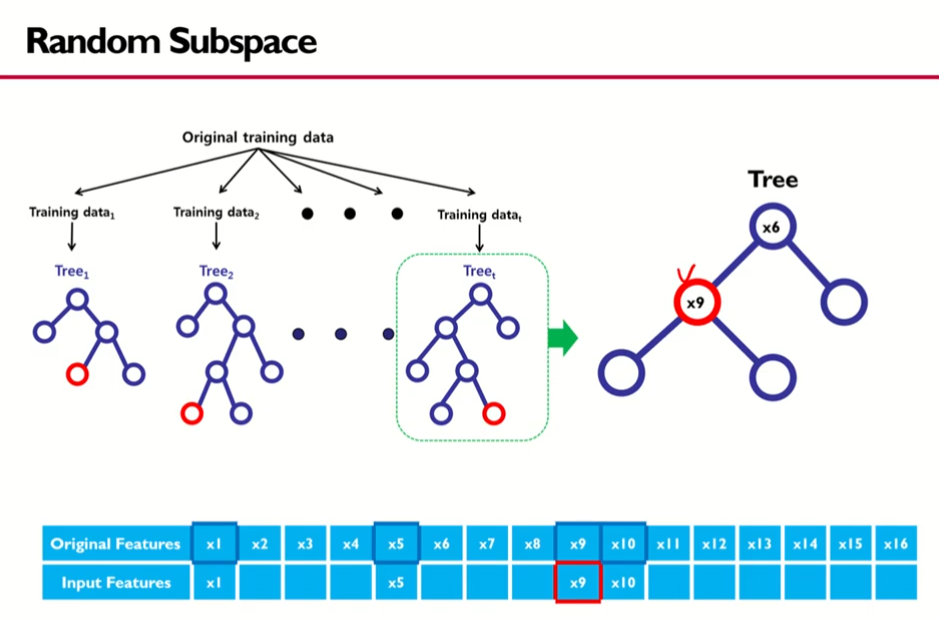
1. 원래 변수들 중에 모델 구축에 쓰일 입력 변수($x_m$)를 무작위로 선택
- ex> $x_1, x_5, x_9, x_{10}$을 선택
2. 선택된 입력 변수 중에 분할될 변수를 선택 -> 일반트리의 분할점s와 분할변수j를 선택하는 것과 동일 -> 노드에 대해 분할됨
- ex> 위에서 선택된 4개의 변수 중에 1개를 고른다. 여기서는 $x_6$을 선택함
- 두개의 노드가 생기고 그 두개의 노드에 대해 각각 랜덤하게 $x$ 4개가 선정됨
- 이번에는 $x_1, x_5, x_9, x_{10}$이 선택되었고 이중에서 살펴보니 $x_9$가 가장 좋더라.
- 이런식으로 모든 변수를 고려하는 것이 아닌 일부만 고려한다.
-> 16개의 변수가 있었으나 4개씩 랜덤하게 선택하고 그 중에서 가장 좋은 변수를 선택하는 과정을 거침, 이를 Random Subspace라고 한다.
(랜덤서브스페이스: 랜덤하게 서브스페이스를 찾는다.)
3. 이러한 과정을 full-grown tree가 될때까지 반복

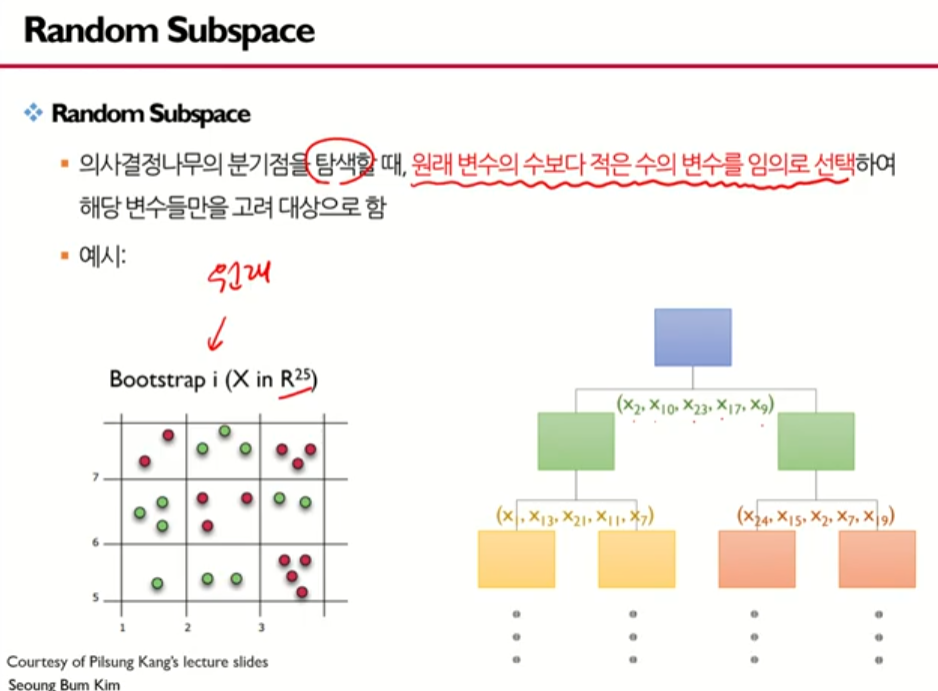
• 16개 중 4개 선택하는 것처럼 적은 수를 임의로 선택해서 분지를 수행함
• i번째 부트스트랩으로 얻어진 i번째 부트스트랩 셋
• $R^{25}$는 25개의 데이터가 있음을 의미
• 여기서 랜덤하게 $x$변수 5개를 선택해서 가장 최고의 분할변수와 분할점을 찾아 분지를 하고.. 쭉쭉쭉 이어짐
  
• 배깅을 통해 다양성을 확보하고 랜덤 서브스페이스를 통해 랜덤성을 확보하였다.
• 랜덤 포레스트와 앙상블 모델이 좋게 작용되려면 다양성과 랜덤성이 확보되어야 하는 것이 큰 전제인데 랜덤 포레스트가 그 정당성을 확보한 케이스

Generalization Error

• $\bar{p}$ : 개별 베이스모델이 서로 독립이면 좋음 -> 즉, 평균 상관관계가 작으면 좋은 것
• 우항이 최댓값
• s는 개별트리의 정확도가 높을수록 s는 증가한다(올바로 예측한 트리가 많고 잘못 예측한 트리는 적어 그 차이가 클때), s(분모, 분자의 빼준값)가 커지면 전체적으로 우항의 upper bound가 작아짐
• 따라서 Generalization Error(일반화 오류)를 줄이려면 $\bar{p}$(상관관계)를 줄여 최대한 독립으로 만들던지 s를 크게 만들던지 하면 된다.

랜덤 포레스트의 중요변수 선택법

• 선형회귀 같은 경우 에러가 정규분포를 따른다던지, 로지스틱회귀 모델은 어느 분포에 근거한다던지와 같은 확률분포를 가정하고 있기 때문에 통계적인 추론이 가능하다. (통계적으로 중요하다, 안중요하다 해석가능)
• 랜덤포레스트는 의사결정나무를 기반으로 가정하고 있는데 이는 전혀 확률분포를 가정하지 않고 있다. 이는 순수한 넌파라미터모델(비모수적 모델)이다.
  

OOB (out of bag)

• 내 가방에 없는 데이터 = 부트스트랩에 선택되지 않는 데이터 (포함되지 않아서)
  
  
• (1) 개별 트리가 생성되었으면 OOB 데이터를 생성트리에 넣어서 에러를 계산해봄(OOB error), $r_t$개의 oob 에러가 생성됨, r은 원래데이터에서 oob만 계산한 것
• (2) 원래있는 변수의 값과 다르게 뒤섞음, e는 특정 변수의 값들을 뒤섞은 것, 뒤섞은 다음에 에러를 봄
• (3) $d_i$는 뒤섞은 에러에서 원래데이터 에러를 뺀 것, 절대적인 차이가 중요하므로 양변에 절대값 취해줘도 됨
  -> 이 차이가 크다는 것은 해당 변수가 다른 값으로 대체됐을 때 성능이 굉장히 안좋아진다는 말(에러가 굉장히 커진다.)
  - 차이는 t개가 나옴, 그 차이의 $\bar{d_i}$ (평균)을 구하고 $S^2_{d}$(분산)을 구한다.
  -> $\bar{d_i}$값이 크면 해당 변수는 중요한 변수라는 뜻
• (4) $\bar{d_i}$가 혹시 크더라도 분산이 크면서 크기 때문에 페널티를 주겠다. $X_i$의 변수 중요도 $v_i$가 작아질 수 있다. 분산은 페널티를 주는 스케일의 역할을 한다고 보면 되고 핵심은 차이($d_i$)나 차이의 평균($\bar{d}$)이 크면 해당변수는 굉장히 중요함을 의미한다.
• 랜덤 포레스트의 각 변수 $X_1, X_2...X_{20}$에 대한 변수 중요도 $v_1, v_2...v_{20}$가 나오고 그에 대해 가장 큰값, 가장 중요한 변수를 찾을 수 있다.

하이퍼 파라미터

• 선형회귀모델이나 로지스틱회귀모델에서는 $\beta$값이 있었고 뉴럴네트워크에서 알고리즘을 결정했던 $w$값 있었다. 이는 유저가 아닌 알고리즘으로 결정하였다.
  - 이러한 파라미터는 랜덤 포레스트 모델에는 없다.
• 랜덤포레스트에서 유저가 결정해야 하는 파라미터는
  -1. Decision Tree의 수: 베이스 모델로 의사결정나무를 사용해야 한다고 했는데 그것을 몇 개로 해야할 것인가?
  => 딱히 정해져있지 않고 책마다 다르지만, 대략 2,000개 정도의 decision tree가 필요하다고 봄 (러프한 가이드라인, 소장님 소견: 많이 구축해보았는데 어떤 경우는 500개 정도만 써도 충분한 결과가 나올 때도 있고, 어느때는 5000개, 1만개 이상 써야 원하는 결과가 나올 때도 있었다.)
  -2. 무작위 선택 변수의 수: 랜덤 서브스페이스를 구현하기 위해서 무작위로 변수를 뽑았는데 그 변수를 몇개를 뽑아야 하는가? (위의 예제에서 16개 중 4개 뽑듯이, 4개는 사람이 결정한 것)
  => 마찬가지도 딱히 정해진 것은 없으나 어떤 문헌에 의하면 분류모델에서는 $\sqrt{변수의 수}$, 회귀모델에서는 $변수의 수/3$(예를들어 변수의 수가 18개 인 경우, 무작위로 선택하는 변수의 수는 6개 정도가 됨) (러프한 가이드라인, 결국 유저가 결정해야 하는 것이기 때문에 trial and error 스텝이 필요하다.
  

랜덤포레스트 알고리즘

• $B$ (부스트랩의 갯수): 부트스트랩을 라지B만큼 생성하고 그만큼의 개별 의사결정나무를 만들겠다는 것
• 1번 i: m < p 아야함!
• 2번: 트리를 앙상블할 것임
• 3번: aggregating(집계)를 어떻게 할 것인가?
• 회귀모델은 이견없이 간단함, 각각 개별 y값으로 나온 것들의 평균을 취함
• 분류모델은 여러가지 안이 나올 수 있는데 그 중 많이 쓰이는 3가지 설명(윗쪽): 다수결 원칙 외

2. 부스팅

• boosting: 점점 더 건강해진다, 강건해진다, 빵빵해진다😃
  -> 단계를 거치면서 모델이 더 정확해진다는 의미
  
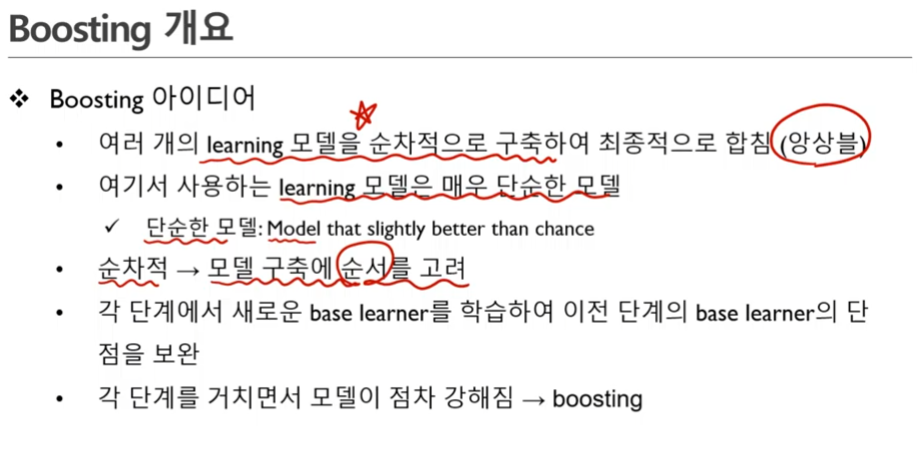
• 이진분류기에서 정확도가 0.5보다 조금 좋은 모델을 단순한 모델이라고 함
  
• Adaboost: 가장 기본이 되는 모델, 에이다부스트만 제대로 이해하면 나머지는 아이디어를 조금씩 더하는 것

1. Adaptive Boosting (Adaboost)

• 에이다부스트 알고리즘
• $W_i = \frac{1}{n}$: 여기서 n은 데이터의 갯수, 모든 데이터의 관측치의 가중치를 동일하게 주겠다.
• $y_i$는 우리가 가지고 있는 레이블, $h_j$는 모델에서 나온 관측값
• 같지 않은 경우에만 count를 하겠다.
• $\alpha$와 $L$의 관계
  - loss fuction이 0.5라는 것은 반밖에 못맞춘 경우(매우 헷갈린 경우)
  - L값이 0인 경우는 perfect한 경우, 알파는 크게 무한대로 간다.
  
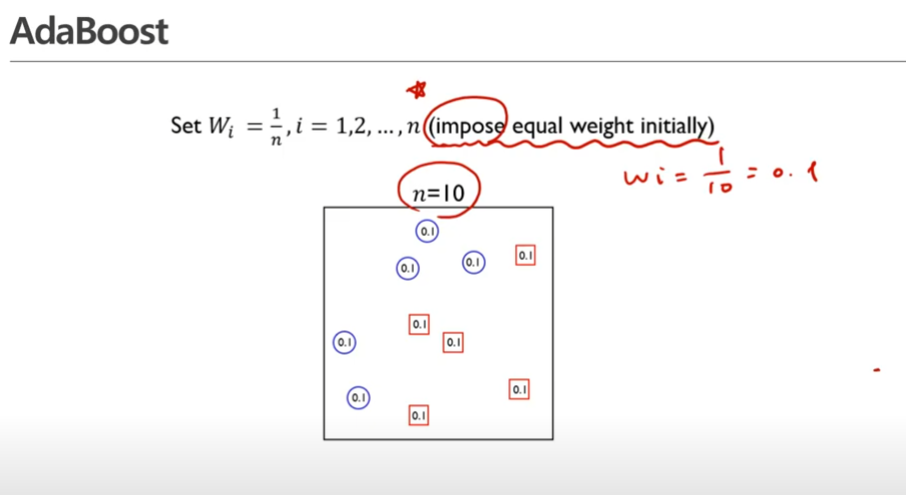
• 모든 관측치의 가중치는 초기에 $\frac{1}{10}$로 주어짐
  impose equal weight initially : 초기에 모든 가중치를 똑같이 부여한다!
  
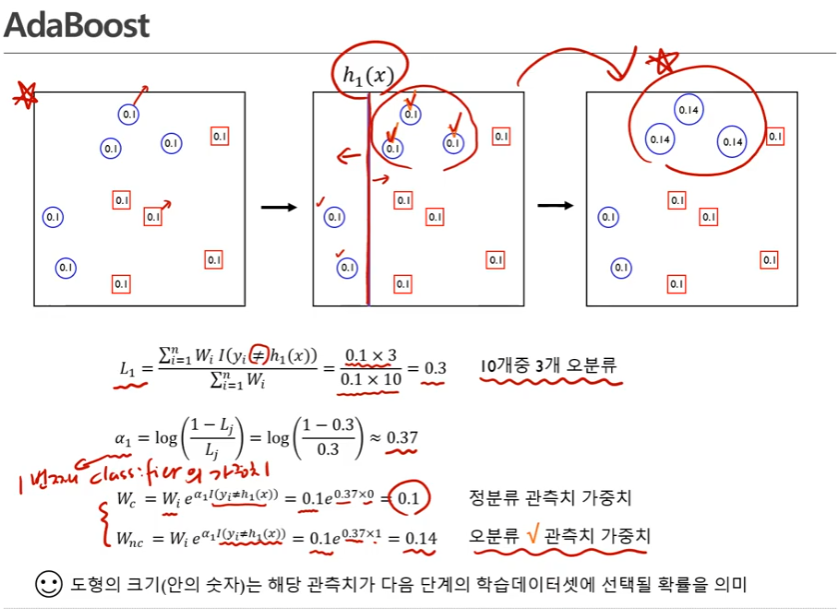
• 그 다음에는 앞서 정의한 weighted fuction을 최소화하는 베이스모델을 찾는다.
  - 부스팅에서 많이 쓰이는 베이스 모델은 디시젼 트리(컨스탠트한 간단한 모델)
• 동그라미 클래스, 네모 클래스 문제
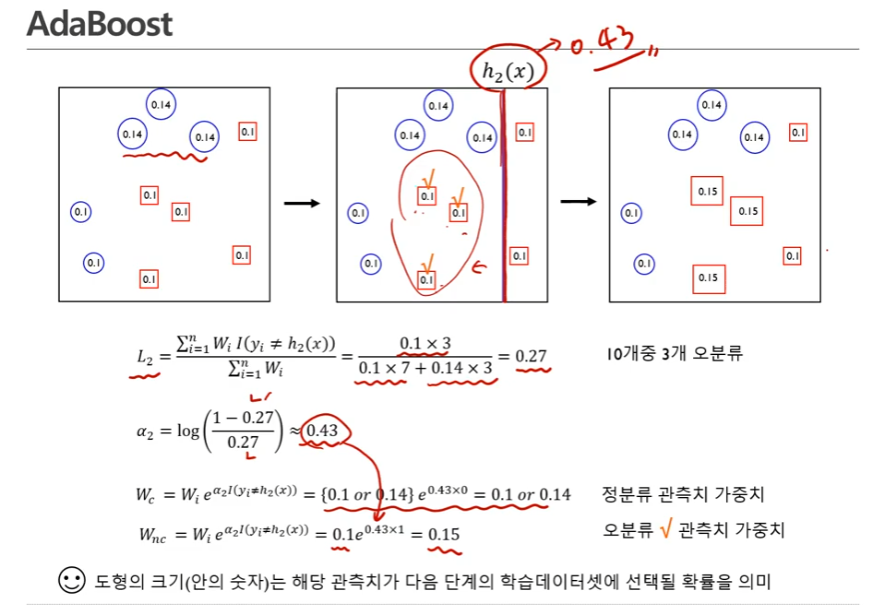
• 2번째 그림상에서 $h_1{(x)}$ 분류기를 기준으로 오른쪽 파란색 동그라미 3개가 오분류됨 (왼쪽은 파란색 동그라미, 오른쪽은 빨간색 네모이므로)
• $L_1$의 분모는 가중치에 대한 합, 모든 관측치가 10개니까 10을 곱해줌
• 분자설명: I(indicator fuction): 실제 $y$값과 모델로부터 나온 레이블$h_1{(x)}$이 서로 다를 때만 1이됨, 오분류한게 3개라서 0.1이 3개 있는 것
• 알파: 첫번째 분류기의 가중치
  -정분류 관측치 가중치는 $y=h_1{(x)}$이 0이어서 0.1로 동일함
  -오분류 관측치 가중치는 $y=h_1{(x)}$이 1이어서 가중치가 0.14가 됨
• 오분류한 관측치 가중치의 크기가 커졌다.
  
• 계속~
• 새롭게 변화한 관측치를 가지고 새로운 classifier를 만들 것임
• $h_2{(x)}$: 2번째 분류기가 구축됨
• $L_2$: 2번째 분류기를 통해 나온 비용함수, 오분류된 것 분류기 왼쪽의 네모 0.1 3개
• $h_2{(x)}$: 2번째 분류기의 가중치가 0.43($\alpha$값)
• 가중치에 대해 업데이트하는데 오분류된 것만 없데이트 됨, 오분류된 것이 3개이므로 3개에 대한 관측치만 변할 것임
  
• 3단계까지 끝남, 0.1이었던 가중치가 제각각으로 바뀐 것을 볼 수 있음
  
• 베이스러너(분류기,모델)가 3개가 생김
• 3개의 모델(분류기,$h_1{(x)},h_2{(x)},h_3{(x)}$)의 가중합을 취하면 어떤 모델이 만들어짐, 여러개의 모델을 합쳐서 하나의 모델을 만듬(앙상블)
• 모든 레이블이 다 잘 분류된 perfect한 상태
  
• Adaboost algorithm 정리
• 정분류한 관측치에 대해서는 가중치를 그대로 두고 오분류한 관측치에 대해서만 가중치를 증가시킴 -> 학습데이터의 가중치가 바뀜, 두번째 모델을 만들때에는 오분류된 가중치에 대해 가중치를 더 둠
• $m$은 분류기의 갯수, 앞선 예에선 3개, 갯수를 먼저 정하고 m개의 분류기가 얻어지면 그것의 가중합을 구한다.
  
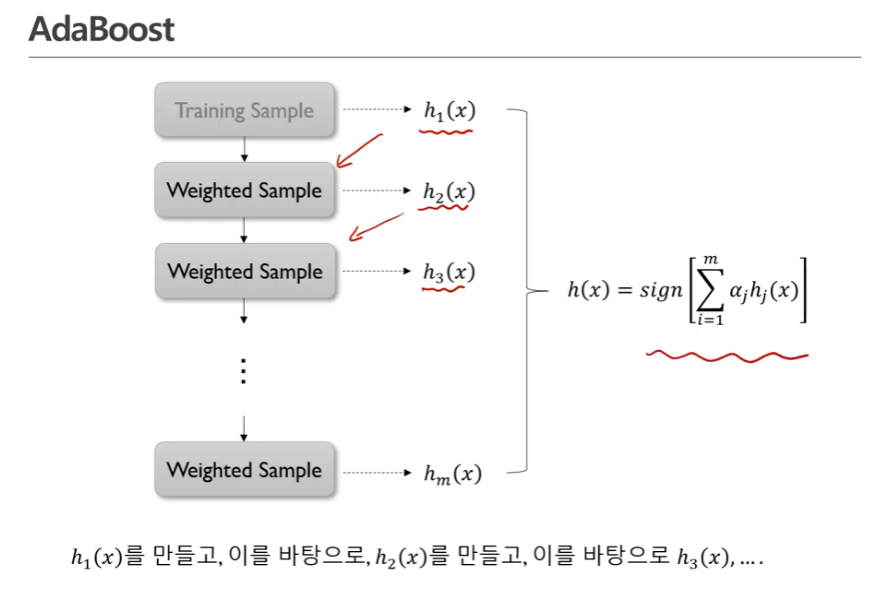
• 시퀀셜하게 순차적으로 모델을 구축

배깅 vs 부스팅 비교

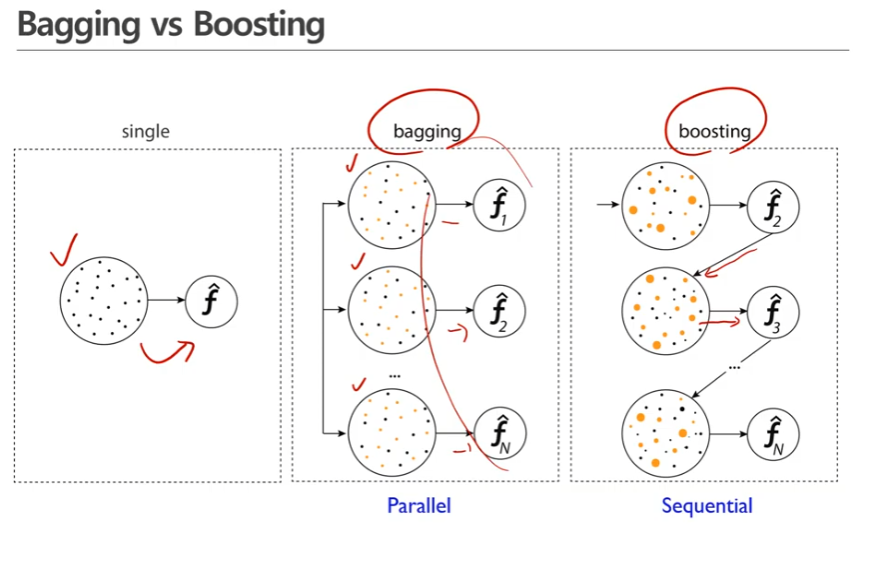
• 싱글모델: 한 개의 학습데이터로 한 개의 모델을 만든 것
• 배깅: 한 개의 학습데이터로부터 parallel하게 여러개의 샘플을 만들어 그로부터 각각 모델을 구하고 이 모델의 가중합을 취함 ex>대표적인 예: 랜덤포레스트 -> 부트스트랩을 이용함
• 부스팅: 하나의 학습데이터가 있으면 그로부터 모델을 만들고 거기서부터 나오는 정보를 가지고 새로운 샘플을 만듬(새로운 샘플을 만들었다는 것은 가중치를 변경[업데이트]했다는 것), 이 작업을 반복함(가중치업데이트 -> 새로운 모델 만들기) 이를 통해 나온 모델들을 다 더하면 이것이 부스팅 모델이 됨

2. Gradient Boosting Machines (GBM)

25:22~ 통해

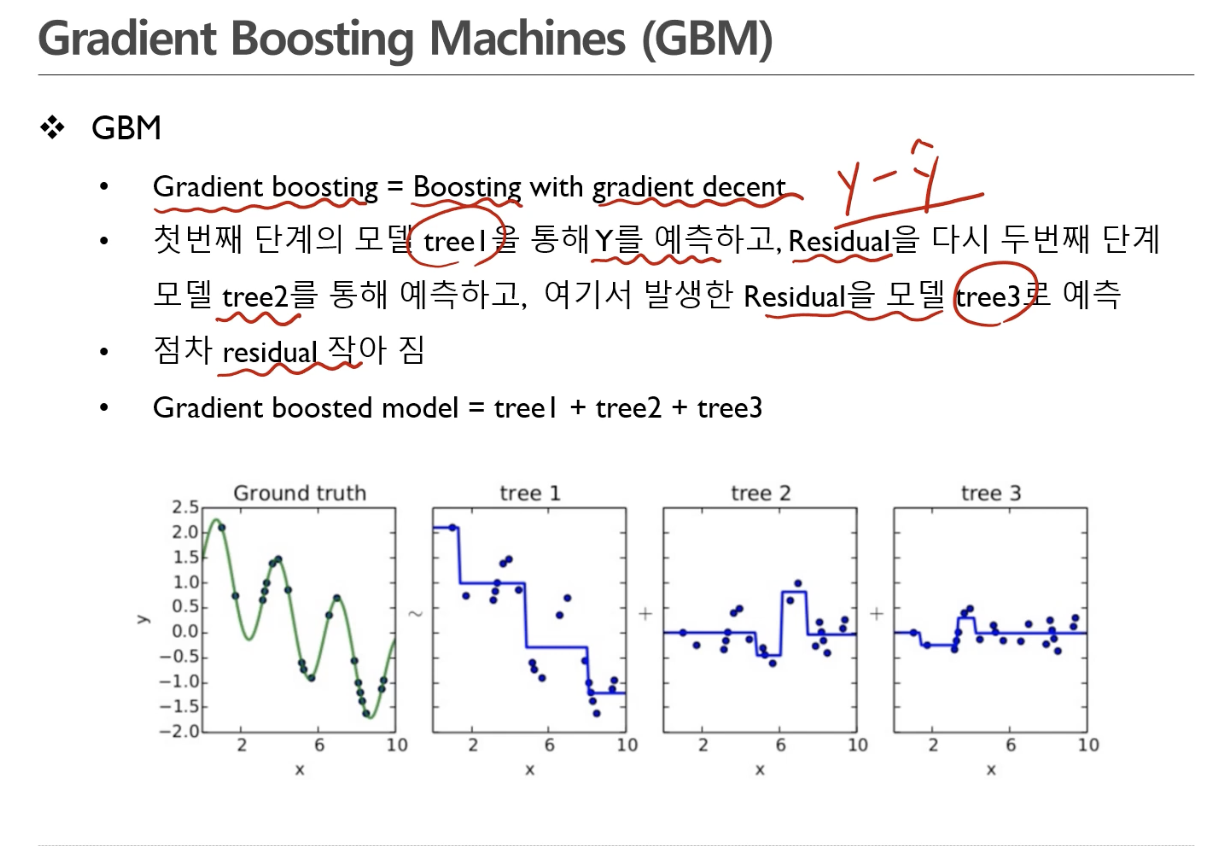
• 경사하강을 통한 부스팅

• Residual = y- y햇
  레지듀얼이 작아지면 모델의 설명이 자세해진다.

• Q.왜 그레디언트인가?
  

그레디언트 = 미분
로스함수를 $f(x_i)$로 미분

실제값과 모델로부터 나온 예측값이 residual -> 그레디언트에 마이너스를 취하면 리지듀얼이됨 (네가티브 리지듀얼)
리지듀얼이 네거티브 그레디언트(마이너스 그레디언트)이다!

다시 정확하게 듣기
$f_1(x)$
$f_1(x)$는 디시젼 트리
리지듀얼을 모델링한 것
$f_1(x)$은 러프한 모델
$f_2(x)$는 $f_1(x)$에서 놓친 부분을 추가함
$f_3(x)$는 $f_1(x)$, $f_2(x)$에서 놓친 부분을 추가함

빨간색선 -> 디시전 트리로부터 나온 결정경계
초록색점 -> 빨간색점과 파란색점의 차이

• 이런 식으로 쭉 열거
• 18번째 됐을 때는 굉장히 정교해짐, 리지듀얼값이 거의 0에 깔림

36:18~ 알고리즘에 대해

3. XGboost

4. Light gradient boost machine (Light GBM)

5. CatBoost (CAT)

(김용담, 6/13 목)

• 실제 데이터 분석 대회에서 가장 많이 사용하는 효과적인 회귀 모델
• 모델 자체서 Categorical feature를 사용할 수 있다.
• 디폴트 파라미터 설계가 잘 되어있어 파라미터 튜닝이 쉬움
• GPU 사용 최적화가 잘 되어있음
• 사용성이 높음

캣부트의 하이퍼 파라미터

• 주요 파라미터
  -> 딱히 바꿀 건 없다.
• border_count: XGBoost의 버킷사이즈와 비슷
• 공식 문서에 있는 파라미터 디자인, 실제 옵튜나를 통해서

GBM Comparison

이미지 삽입

• Q. 실제 데이터 분석 대회에서 어떤 모델이 가장 좋을까?
• 실험을 많이 해보는 게 중요!
• 1. 강사님st. N=10,000개보다 크면 XGBoost사용, 작으면 LightGBM 사용
• 2. 이와 별개로 Categorical feature가 50% 이상이면 CatBoost 사용
     => 사람마다 70%이상(거의다) 되어야 캣부스트가 낫다 하는 사람도 있고 카테고리컬이 적어도 캣부스트가 성능이 낫다 하는 사람이 있음, 데이터 갯수와 상관없이 3중 아무거나 상관없다 등 다양한 케이스
• 3. 많이 돌려서 써본 결과 만단위, 10만단위, 100만단위 써봤을 때 XGBoost, LGBM 속도 차이는 큼 -> 대용량에서는 LGBM 쓰는 것을 추천
• 모두 GPU 액셀러레이션을 쓰는 게 좋으나 LGBM 같은 경우 코랩에서 GPU 액셀러레이션이 잘 안됨, 캐글 노트북에서는 잘됨
• 4. 데이터가 1000개보다 작으면 Random Forest 써도 괜찮음
     -> 랜덤 포레스트가 강력함
  • 사이킷런으로 1000개보다 적은 경우 돌리면 1초도 안되서 나옴, 속도이슈는 신경쓰지 않아도 됨
• 실습: CatBoost를 사용해보자

GBM 계열 정리

• 쓰면 쓸수록 어렵다.
  - 처음에는 복붙하거나
• 적당한 범위 설정이 어렵다. 이는 짬에서 나오는 노하우, 하면서 익혀야함
• 실제 사용할 수 있는 방법론

실제 실무에서 ML을 어떻게 쓰는가?

데이터베이스(DB)에 대한 이야기

1. Data Lake: 데이터 소스(data source)에서 발생하는 거의 모든 데이터를 수집하는 DB (거의 모든 데이터를 담음, 6500만개 적재, 보통 NoSQL ex> AWS Redis, kafka 많이씀, 그 외 많이있음 => 과거에 지나가면 못담으니 일단 디비에 다 때려넣자, 적재)
   • 이런 회사가 꽤 많음, 큰 IT 기업
   • 데이터가 돈이고 가치이기 때문이다.
   • 데이터를 돌리는 일은 차후 문제
2. Data Warehouse: 데이터 레이크에서 필요한 데이터 정재해서 적재한 DB (RDBMS ex> 오라클DB(best!)를 가장 많이 쓰고 돈 없는 회사는 MySQL, Postel~, MariaDB)
   • 데이터 웨어하우스는 모두 관계형 데이터베이스

• 데이터가 한 곳으로 모이는 곳(전사)에 데이터레이크와 데이터 웨어하우스가 있다. ex> 삼성전자
  - 데이터가 한 곳에 모여야(중앙집중적) 데이터를 관리 할 수 있기 때문
  • 데이터 센터를 엄청 크게 짓고 거기에 데이터를 다 때려넣고 필요할 때마다 꺼내서 주는 형태

3. Data Mart (Table): 필요에 의해(분석 목적에 맞게) 만든 DB -> 분석이 필요할 때 (보통RDB, 이미지나 텍스트 데이터 일때는 NoSQL ex>MongoDB) 데이터 마트(VM, 디비서버)를 띄워서 데이터 웨어하우스에서 SQL로 필요한 데이터만 뽑아서 디비서버에 적재 후 데이터 마트에 공유해서 데이터를 제공하고 분석끝나면 DB내림(리소스라서)
   • 분석할 때 데이터 마트만 쓰면 됨
   • 작은 회사는 데이터량이 적고 중앙에서 관리 안할 때

---

<앙상블 및 랜덤 포레스트>

1. 투표 기반 앙상블 분류기

2. 배깅과 페이스팅

3. 랜덤 포레스트 엑스트라 트리

4. 부스팅

5. 그래디언트 부스팅 대표 3인방 - XGB, LGB, CatGB

• <연관 시리즈 링크>

• 랜덤 포레스트 jane15.log 시리즈 > 사이킷런 Sklearn > 8. 랜덤 포레스트 (Random Forest)

• 앙상블 jane15.log 시리즈 > 사이킷런 Sklearn > 9. 앙상블 (Ensemble)

• 배깅 jane15.log 시리즈 > 사이킷런 Sklearn > 10. 배깅(Bagging)

• 부스팅 jane15.log 시리즈 > 사이킷런 Sklearn > 11. 부스팅 (Boosting)

• 스태킹 jane15.log 시리즈 > 사이킷런 Sklearn > 12. 스태킹 (Stacking)