CH.9 오차역전파 (back propagation)
-
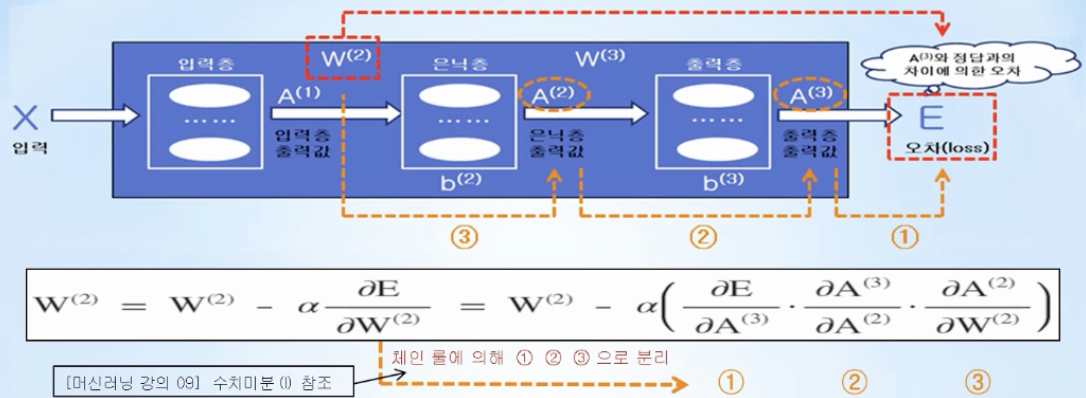
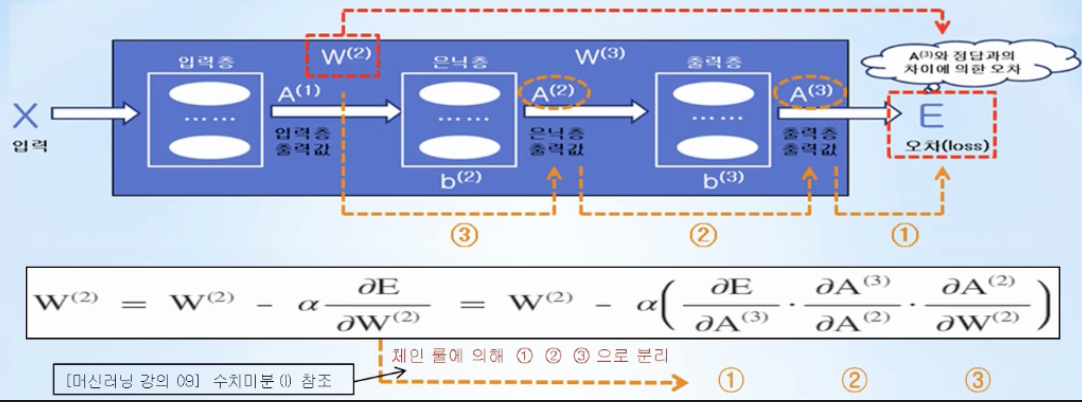
가중치나 바이어스가 변할 때 최종오차가 얼마나 변하는지를 나타내는 편미분을, 체인룰(chain rule)을 이용하여 위 식의 1,2,3 처럼 국소(local) 미분으로 분리한 후, 국소 미분을 수학 공식으로 나타내서 계산하는 방법
-
오차역전파는 수치미분을 사용하지 않고 행렬로 표현되는 수학공식을 계산하기 때문에 빠른 계산이 가능함
-
각 층의 선형회귀값과 출력값
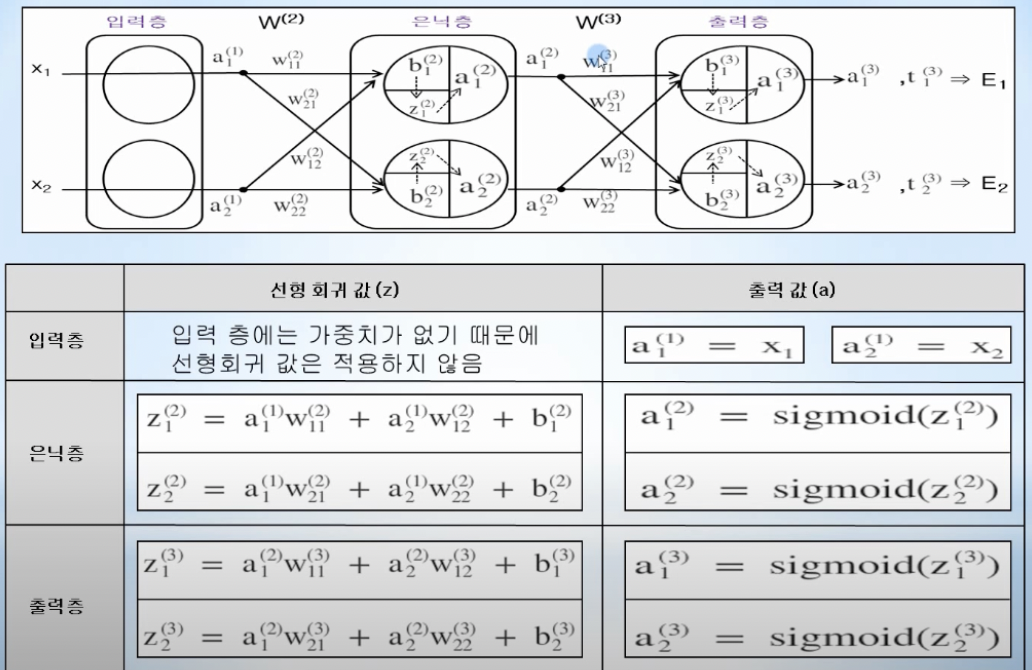
-
시그모이드 함수 미분

- 시그모이드를 편미분하면 sigmoid(z) * (1-sigmoid(z))
- 오차역전파에서의 활용
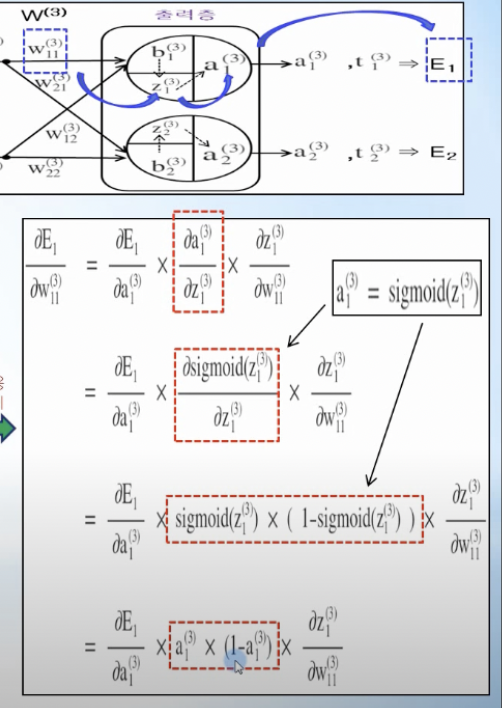
- w11(3)가 E1에 미치는 영향은 chain rule에 의해 a1이 E1에 미치는 영향, z1이 a1에 미치는 영향, w11(3)이 z1에 미치는 영향의 곱으로 표현 가능함 (서로 연관되어 영향을 주기에. 화살표를 보면 직관적 이해 가능)
-
최종 손실(error)값 E, 가중치 W, 바이어스 b
- E1은 a1에만 영향을 받고, E2는 a2에만 영향을 받기에 서로 독립 → E = E1+E2로 표현 가능
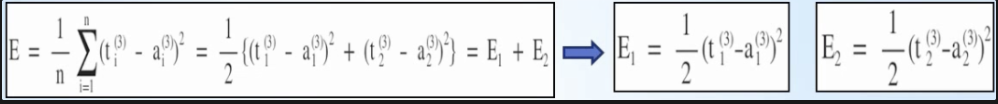
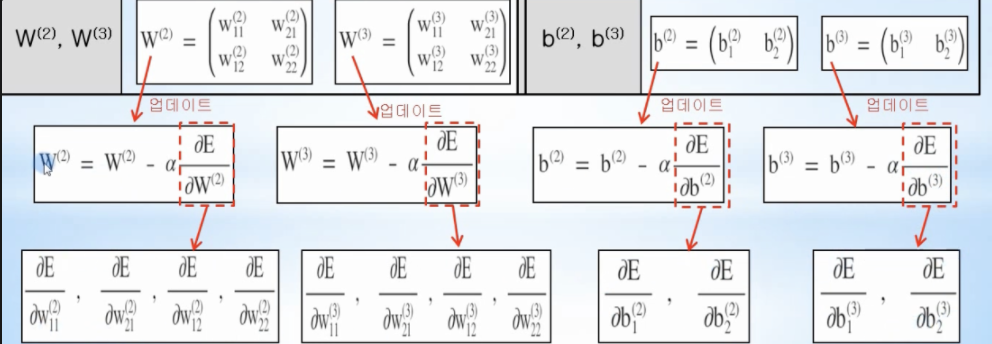
- W, b 각각의 항목에 대해 총 12개의 미분을 해서 W, b를 업데이트해야 함
- E1은 a1에만 영향을 받고, E2는 a2에만 영향을 받기에 서로 독립 → E = E1+E2로 표현 가능
-
출력층 오차역전파 공식 유도

- w11이 변할 때 E2는 영향을 받지 않음
- chain rule을 이용해 국소미분으로 분리
- 편미분을 곱셈 형태의 수식으로 바꿈
- w12, w21, w22, b1, b2모두 같은 원리
-
출력층 오차역전파 공식을 행렬로 나타낼 수 있음
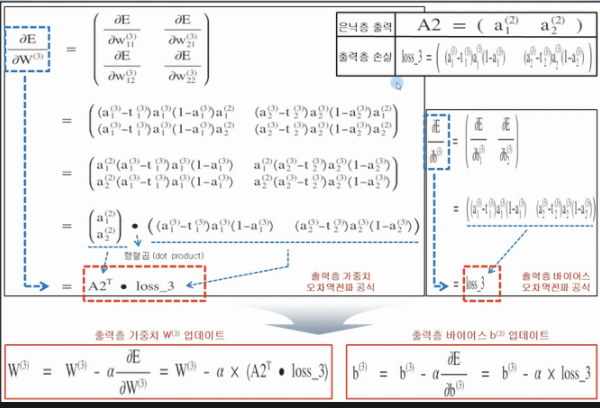
-
은닉층 오차 역전파 공식 유도
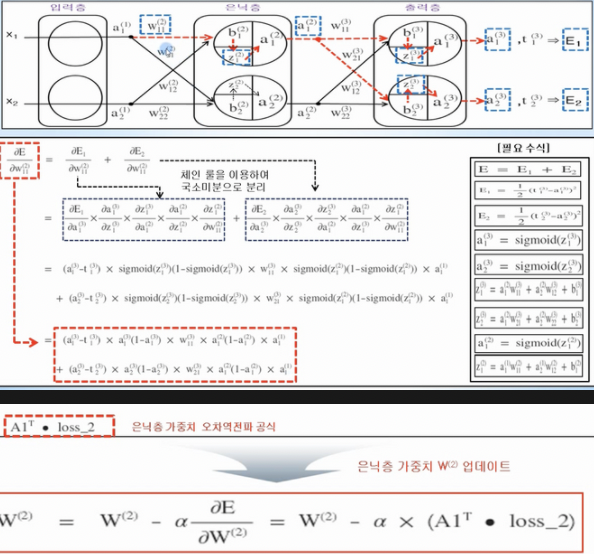
- 출력층과 원리는 같지만, w11은 E1, E2 모두에 영향을 주고, 영향을 주는 부분이 더 많기에 식이 더 길어짐
-
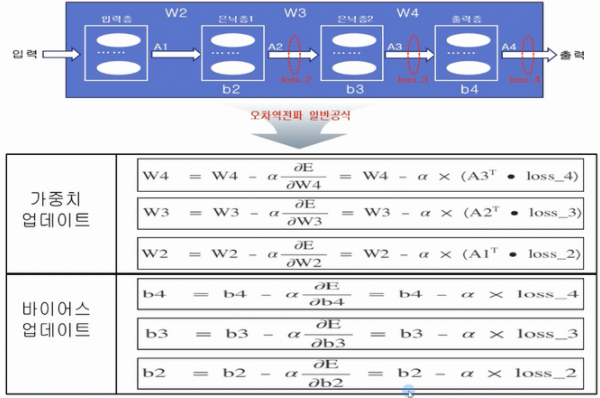
오차역전파 일반 공식