선형대수
스칼라
- Scalar는 숫자와 같은 수치를 의미
- 수학 공식에서는 스칼라 변수를 흔히 x처럼 영문 소문자로 표기
벡터
-
Vector는 여러 개의 수치(성분)로 이루어진 1차원 배열
-
수학에서 벡터는 성분들이 수직으로 배치된 버전과 수평으로 배치된 버전으로 구분
-
수평 방향의 벡터를 행벡터(row vector)
-
x = [x0, x1, x2]
-
수학에서 벡터라고 하면 일반적으로 성분들이 수직으로 배치된 열벡터(column vector)를 뜻함
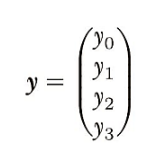
-
벡터의 각 성분을 좌표공간의 좌표성분, 즉 한 좌표축을 따라 나아간 거리로 해석하기도 한
다. -
예를 들어 3성분 벡터를 3차원 공간의 한 점을 표현하는 데 사용할 수 있다.
-
x = [x, y, z]
-
x를 x축을 따라 나아간 거리, y를 y축을 따라 나아간 거리, z를 z축을 따라 나아간 거리로 간주하면 이 벡터는 3차원 공간의 한 점을 규정하게 된다.
-
따라서 3성분 벡터는 3차원 공간의 모든 점을 고유하게 식별할 수 있는 데카르트 좌표에 해당한다.
-
벡터들의 성분들을 특징(feature)을 나타내는데 사용된다.
-
특징이란, 모형이 어떤 유용한 출력을 산출하는 과정에서 사용하는 , 표본이 가진 어떤 성질 또는 측면을 뜻한다.
특징공간(feature space)
- 특징공간은 가능한 입력값들의 집합을 뜻한다.
- 모형을 훈련하는데 사용하는 훈련 데이터 집합, 줄여서 training set은 모형을 실제로 적용할 때 만나는 모든 가능한 입력으로 구성된 특징공간을 정확하게 반영하는 데이터 집합이어야 한다.
- 하나의 특징 벡터는 이 n차원 특징 공간의 한 점에 해당한다.
- 여기서 특징 공간의 차원 n은 곧 특징 벡터의 특징 개수이다.
차원의 저주
- 특징의 수가 많아 질수록 축의 개수가 많아지고 차원이 커진다.
차원이 증가함에 따라 모델의 성능이 하락하게 되고, 이를 극복하기 위해 휠씬 더 많은 데이터를 필요하게 되는데, 이를 ‘차원의 저주’라 부른다. - 데이터의 차원이 증가할수록 데이터를 표현할 수 있는 공간은 기하급수적으로 증가하는데
반해 데이터의 수는 변하지 않기 때문에 발생한다. - 즉 차원이 증가함으로 인해 데이터가 차지하는 공간이 미비해지고 각 데이터 사이의 거리가 멀어지며 데이터의 밀도가 급격하게 낮아져 발생하는 현상
- 빈 공간은 컴퓨터가 정보가 없는 상태로 채우는데 이로 인해 모델링 과정에서 저장공간과
처리 시간이 불필요하게 증가되어 성능이 매우 저하된다. - 해결 방안으로 데이터를 밀도가 충분히 높아질 때까지 데이터의 크기를 키우면 되지만, 데이터가 무한히 있지도 않고, 컴퓨터의 성능이 그만큼 더 필요하기 때문에 차원 축소나 변수 선택같은 방법을 사용한다.
행렬
- 수치들의 2차원 배열

- 이런 행렬을 3 X 4 행렬이라고 표기
텐서
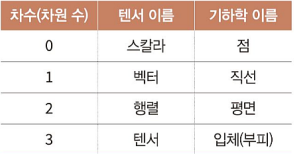
- 스칼라는 차원이 없고, 벡터는 1차원, 행렬은 2차원이다.
- 그렇다면 차원이 셋 이상인 수학적 객체를 통칭해서 텐서(tensor)라고 부른다.
- 텐서의 차원 수는 텐서의 order(차수)를 결정한다.
- 텐서의 차수를 행렬의 차수와 혼동하면 안된다. 3차원 텐서의 차수는 3이고, 행렬은 2차 텐서, 즉 차수가 2가 2인 텐서이다.
- 아래는 차수가 3인 텐서의 예이다.
t = np.arange(36).reshape((3,3,4))- 아래 표는 차수들의 관계