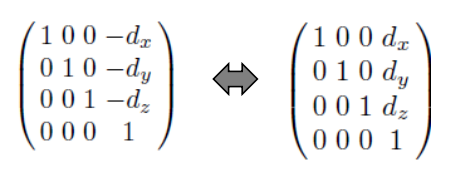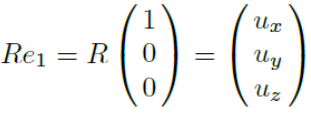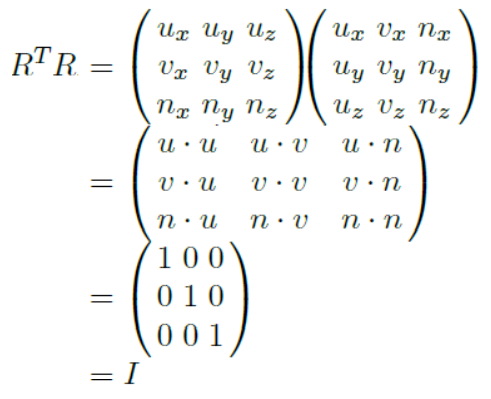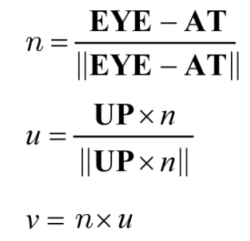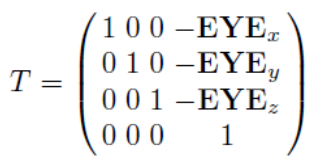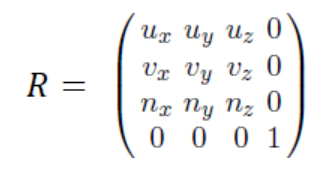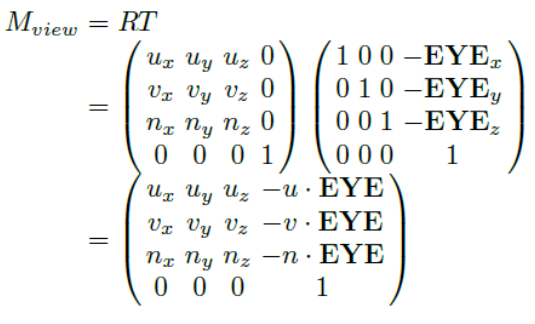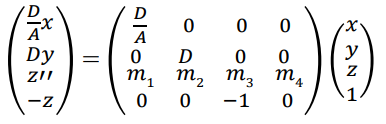이 시리즈는 3차원 그래픽스에 대해 공부한 내용들을 담고 있습니다.
참고 자료 :게임 프로그래밍을 위한 3차원 그래픽스 (한정현, 홍릉과학출판사)등
렌더링 파이프라인
파이프라인(Pipeline) : 한 단계의 출력이 다음 단계의 입력으로 사용되는 일련의 데이터 처리 구조
렌더링 파이프라인은 3차원 장면을 입력으로 받아 이를 2차원 형태로 바꾸고,
2차원 폴리곤 내부를 차지하는 픽셀의 색을 결정하여 최종 영상을 생성한다.
렌더링 파이프라인의 주요 요소는 다음과 같은 순서로 구성된다.
정점 처리 -> 래스터화 -> 프래그먼트 처리 -> 출력 병합
정점 처리, 프래그먼트 처리 단계는 programmable하지만
래스터화, 출력 병합 단계는 hardwired하다.
정점 처리Vertex processing
vertex buffer에 저장된 모든 vertex에 대해 변환transform 등의 연산을 수행하는 단계
래스터화Rasterization
vertex processing으로 얻어진 vertex에 의해 정의된 폴리곤의 내부를 차지하는 프래그먼트를 생성하는 단계
프래그먼트 : 컬러 버퍼에 저장된 픽셀을 수정하는데 필요한 데이터의 모음
(ex. 텍스처 좌표)
컬러 버퍼 : 화면을 구성하는 픽셀의 색을 저장하는 버퍼
프래그먼트 처리Fragment processing
프래그먼트를 입력받아 색상을 결정하는 단계
출력 병합Output merging
프래그먼트와 컬러 버퍼에 저장된 픽셀을 선택하거나 결합하여 컬러 버퍼에 저장하는 단계
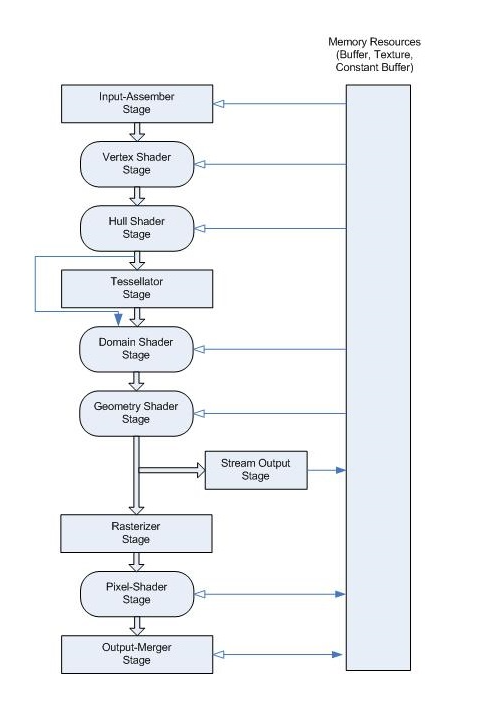
Microsoft Docs - graphics pipeline에 명시된 렌더링 파이프라인은 다음과 같다.
vertex processing은 크게 보면 위 파이프라인에서의
(Input-Assembler Stage ~ Rasterizer Stage 이전) 단계에서 수행된다.
Transform
vertex processing을 위해서는 다음과 같은 공간(좌표계)이 사용되며,
이 과정에서 vertex의 좌표계 변환이 일어난다.
앞으로 살펴볼 것은 이러한 좌표계 변환space change을 수행하기 위한 기초적 수학 지식이다.
Affine Transform
Linear Transform : Scaling + Rotation
Affine Transform : Linear Transform + Translation
간단하게 이해하자면 affine transform은
물체의 축소/확대, 회전, 이동을 일컫는 단어이다.
Scaling
이는 3*3 크기의 scaling matrix이다.
는 각각 x, y, z축별 scaling factor라 하고,
그 값이 1보다 크면 확대, 1보다 작으면 축소를 의미한다.
S에 3차원 좌표 벡터를 곱함으로써 확대/축소scaling된 vertex의 벡터는 다음과 같이 표기할 수 있다.
Rotation
다음은 2차원에서의 회전 행렬이다.
식의 유도는 간단한 삼각함수의 변환을 통해 이루어지니 생략한다.
2차원 회전이 점을 기준으로 이루어진다면, 3차원 회전은 축*axis*를 기준으로 이루어진다.
한 벡터 (x, y, z)가 z축을 중심으로 회전하여 얻어진 벡터를 (x', y', z')라고 하자.
이 때 점의 z좌표는 변하지 않을 것이므로 이다.
따라서 위의 식과 이를 결합한다면 z축에 대한 3차원 회전 행렬 는 다음과 같은 식으로 정의될 수 있을 것이다.
같은 방법으로 를 구할 수 있다.
Translation
좌표 (x,y,z)를 (x+dx, y+dy, z+dz)로 옮기는 변환은 다음과 같이 벡터의 덧셈으로 표현될 수 있다.
그러나 동차 좌표를 사용한다면, translation은 행렬의 곱으로도 표현될 수 있으며, 이를 통해 추후 다른 행렬 계산과의 결합에 용이하게 사용할 수 있다.
동차 좌표Homogeneous coordinates
같은 벡터 상에 위치하는 점을 특정 평면에 projection시킨 경우 두 점은 homogeneous coordinates에 존재한다.
이를 cartesian coordinates에 적용하면 (x,y,z)를 (x,y,z,1)로 표현할 수 있다.만약 네 번째 원소가 1이 아닌 w인 경우 (,,,)으로 표현할 수 있는데, 이 역시 앞선 (x,y,z,1)과 homogeneous coordinates에 있다.
만약 w가 0인 경우 (x,y,z,w)는 벡터를 나타내고, 그렇지 않으면 점을 나타낸다.
homogeneous coordinates를 이용하여 위의 translation에 사용된 3*3 행렬을 다음과 같은 4*4 행렬로 표현할 수 있다.
다른 affine transform에 사용된 matrix들 역시도 위와 같은 방식으로 행렬을 확장하여 사용할 수 있다.
ex. 확장된 3*3 scaling matrix
Inverse matrix
다음은 앞선 affine transform에 사용된 matrix들에 대한 역행렬이다.
Scaling
Translation
Rotation
x, y, z축에 대한 단위벡터 를 각각 {u, v, n}으로 회전시키는 행렬 R이 있다고 가정하자.
행렬 R은 단위행렬 의 각 열벡터인 단위벡터들을 위와 같이 변환시킬 것이다.
즉, R은 다음과 같이 표현될 수 있다.
이 때, 다음의 사실을 고려하여 와 을 곱해보자.
1. 기저를 이루는 벡터는 서로 수직하기 때문에 그 내적의 합이 0이다.
2. 어떤 행렬과 그에 대한 역행렬을 곱하면 그 결과로 단위행렬이 나온다.
위와 같은 과정을 통해 우리는 다음과 같은 중요한 사실을 알 수 있다.
즉, 가 된다.
World Transform
모든 object는 자신의 object space에서의 좌표를 가진다.
이를 별개의 단일 공간인 world space에 모으는 과정이 world transform이다.
homogeneous coordinates를 사용한 덕분에 affine transform은 행렬의 수에 상관없이 서로 결합되어 4*4의 행렬로 표현될 수 있다.
예를 들어 어떤 벡터 x에 대해 회전행렬 R, 이동행렬 T를 이용하여 회전 후 이동을 한 경우, 이를 나타내는 결합된 matrix는 로 표현될 수 있다.
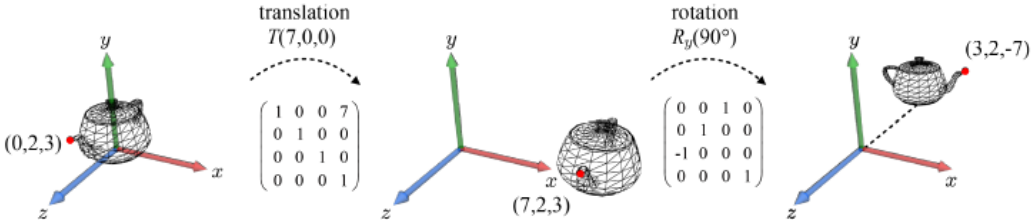
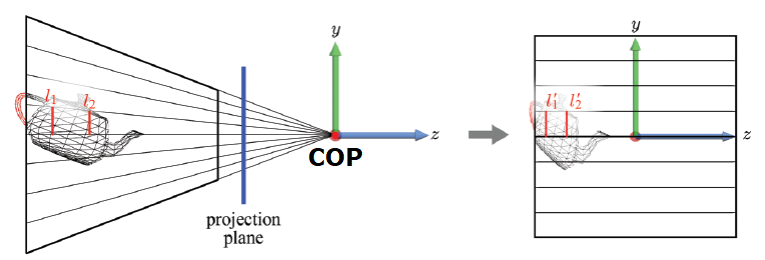
translation을 먼저 수행하는 경우, 이는 후의 linear transform의 결과에 영향을 미친다.
원점이 아닌 좌표에서 linear transform이 수행되는 경우, 좌표의 이동(translation)이 수반되게 된다.아래 그림에서 rotation의 결과로 주전자뿐만 아니라 좌표계 전체가 회전하여 주전자의 위치가 바뀐 것을 확인할 수 있다.
이렇게 결합된 행렬은 해석에도 용이하다는 장점이 있다.
결합된 4*4 행렬의 왼쪽 위 3*3 submatrix는 linear transform(scaling + rotation)을 나타내고,
4번째 column은 translation을 표현한다고 해석할 수 있다.
Euler Transform
에 대한 rotation이 결합된 transform을 뜻한다.
Normal Vector
transform matrix M은 노멀(법선) 벡터의 변환에도 사용될 수 있다.
단, M이 non-uniform scaling(가 모두 같은 값이 아닌 경우)를 포함하지 않은 경우에만 가능하다.
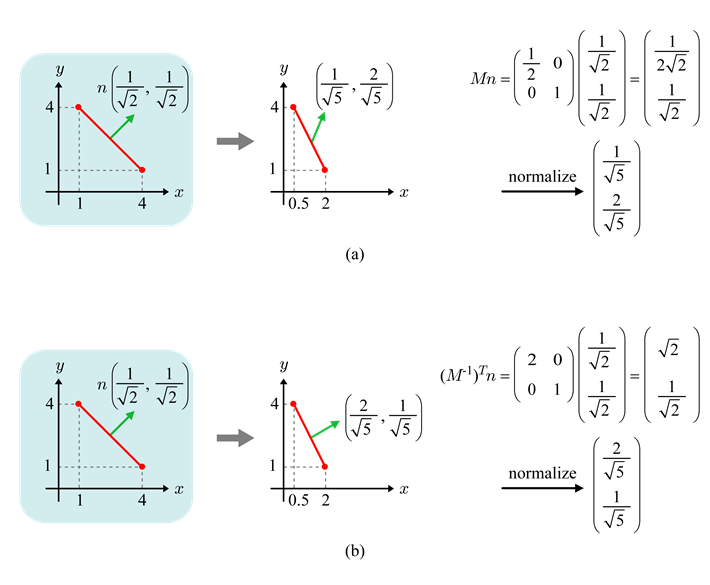
이 경우 M이 아닌 을 사용한다면 노멀 벡터 n에 transform을 적용할 수 있다.
< 증명 >
삼각형 <p,q,r>와 삼각형의 노멀 벡터 n이 있다.
서로 수직한 벡터의 내적은 0이므로
(1)행렬 M에 의해 변환된 삼각형이 <p',q',r'>이라 하면
양 변에 을 곱하면
이를 식 (1)에 대입하면
(2)
식 (2)의 좌변을 전치transpose한다.
(3)식 (3)을 통해 벡터 p'q'가 에 의해 변환된 n과 수직함을 알 수 있다.
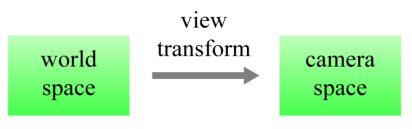
View Transform
world transform을 통해 world space에 모아진 물체들을 원하는 시점viewpoint에서 보기 위해서 카메라의 파라미터를 설정한다.
이러한 카메라의 파라미터는 camera space를 정의하며, world space를 camera space로 변환하는 과정을 view transform이라 한다.
Camera space
카메라는 다음의 세 가지 파라미터를 가진다.
EYE : 카메라의 위치
AT : 카메라가 바라보는 기준점
UP : 카메라의 상단이 가리키는 벡터
위의 식은 카메라의 파라미터를 통해 camera space의 기저 {u, v, n}을 구하는 과정이다.
이 때 {u, v, n}의 크기는 1로 정규화되어 있으므로 orthonormal하다.
Space change
공간 이전Space change은 하나의 공간을 다른 공간으로 재정의하는 것을 의미한다.
World space는 {O, }로 표기하며, O는 원점을 의미한다.
Camera space는 {EYE, u, v, n}로 표기한다.
Camera space {EYE, u, v, n}를 world space {O, }에 겹치기 위해서는 EYE -> O 로의 translation과 {u, v, n} -> {} 로의 rotation이 필요하다.
이 때 camera space 상의 점 p는 space change와 함께 변환되게 되며, 이렇게 변환된 p'의 world space 상 좌표는 space change 수행에 따라 camera space와 world space가 동일해졌기 때문에 그대로 camera space 상의 좌표로 사용할 수 있다.
EYE를 O로 옮기는 translation 벡터는 O - EYE ()로 정의될 수 있고,
따라서 다음과 같은 Translation matrix를 얻을 수 있다.
또한 Camera space의 기저를 World space의 기저로 바꾸는 Rotation matrix는 다음과 같이 얻을 수 있다.
World space의 표준 기저는 이고, 이는 각각 x, y, z축에 대한 단위 벡터이다.
Object space의 기저를 {u, v, n}이라 할 때, 앞선 Inverse matrix에서의 예시와 같이 회전행렬 R을 을 만족하는 행렬이라 하자.이 때, world transform(object space -> world space)과 반대로 R은 world space를 object space로 변환함에 유의한다.
단위 벡터로 이루어진 기저 e = {}를 {u, v, n}으로 바꾸는 회전 행렬이 R이었고( ),
Space change에서 camera space를 world space의 기저로 바꾸기 위한 회전행렬은 의 방향이므로 R의 역행렬이 필요하다.이 때, 였으므로 상단의 rotation matrix의 형태( )가 나타나게 된다.
최종적으로 얻어지는 View transform matrix는 translation matrix T와 rotation matrix R의 결합으로 표현될 수 있다.
Projection Transform
앞선 과정을 통해 World space의 모든 물체가 Camera space로 변환되었다.
world space의 고려는 더 이상 필요가 없으므로 이제부터는 camera space의 기저를 {u, v, n}이 아닌 더욱 익숙한 형태인 {x, y, z}로 표기한다.
이제 camera space를 clip space로 변환해보자.
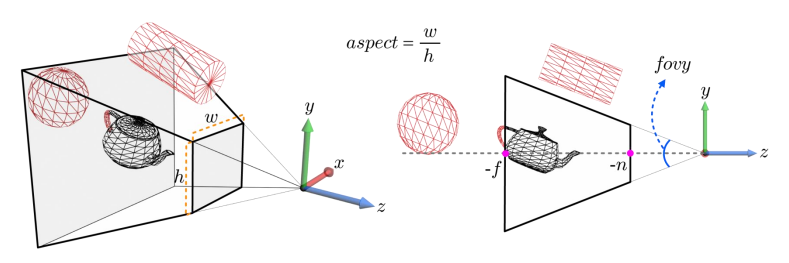
View Frustum
위의 그림과 함께 아래 용어를 쉽게 이해할 수 있다.
View Volume : 카메라의 가시 영역
View Frustum : fovy, aspect, n, f에 의해 결정되는 유한한 크기의 view volume
fovy : Field Of View of Y-axis. y축에 따른 시야각
aspect : view volume의 가로 세로 비율. 종횡비라고도 한다.
n : 원점으로부터 near plane까지의 거리
f : 원점으로부터 far plane까지의 거리
즉, view frustum은 fovy, aspect, n, f의 네 가지 파라미터로 결정되는 잘린 피라미드 형태의 가시 영역이다.
위 그림에서의 view volume은 의 평면plane에 의해 절단되어 view frustum을 형성하고 있는 것을 볼 수 있다.
EYE, AT, UP : 외부external 파라미터
fovy, aspect, n, f : 내부internal 파라미터
View frustum culling
view frustum 외부의 물체를 최종 화면에 나타나지 않게 하여 렌더링 성능을 높이는 전처리 과정을 의미한다.
bounding volume : 복잡한 곡선으로 이루어진 메쉬에 대해 frustum과의 충돌 검사를 더욱 쉽게 하기 위해, 주로 간단한 도형(ex. 구, 직육면체)으로 개별 폴리곤 메쉬(객체)를 감싸는 것을 말한다.
bounding volume이 view frustum의 외부에 있는 경우 해당 객체는 GPU 파이프라인으로 보내지지 않는다.
Clipping
view frustum과 일부가 겹쳐있는 물체에 대해, frustum 외부의 부분은 잘라서clipping GPU 파이프라인에 보내지 않는다.
clipping은 camera space가 아닌 clip space에서 수행된다.
Projection matrix
Projection transform은 view frustum을 2*2*1 크기의 직육면체 view volume으로 변환한다.
직육면체의 xy범위는 [-1,1]이고, z범위는 [-1,0]이다.
이 때 주의할 점은 projection transform의 수행 결과가 2차원이 아닌 3차원 공간으로 나타난다는 점이다.
(3차원 -> 2차원 변환 작업은 래스터화의 perspective division 단계에서 이루어진다.)
위 그림에서 볼 수 있듯 view frustum은 COP(Center Of Projection ; 투영 중심)에서 나오는 projection line의 집합이다.
projection line은 COP와 view frustum 사이의 projection plane에 원근법이 적용된 영상을 형성한다.
View frustum을 2*2*1 크기의 직육면체 view volume으로 변환하는 행렬은 다음과 같다.
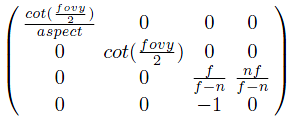
affine transform에 쓰였던 행렬과 다르게 마지막 행이 (0 0 0 1)이 아니다.
< 유도 >
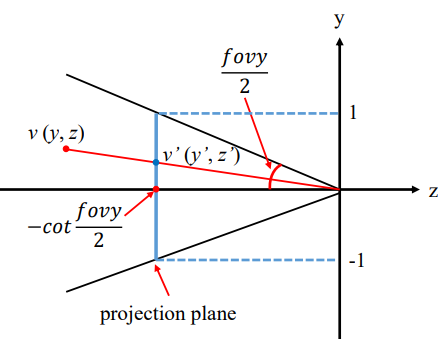
view frustum 내부의 점 v : (x, y, z)에 대해 projection된 v'의 좌표를 (x',y',z')라 하자.
x',y'의 범위는 [-1,1], z'의 범위는 [-1,0]이 된다.
위에 projection plane이 있다고 할 때, 이므로
(1)같은 방법으로
(2)
를 얻을 수 있다.
그러나, 우리는 에 대한 정보가 없으므로 와 를 이용하여 에 대해 정의해야 한다.
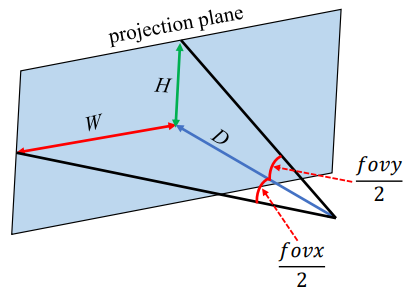
는 종횡비이므로 넓이를 높이로 나누어 구할 수 있다.
(3)
식 (3)을 통해 식 (2)를 와 에 대해 정리하면
(4)따라서 변환된 점 v' = (x', y', z', 1)은 다음과 같이 표현될 수 있다.
v의 각 원소들에 -z를 곱해 v와 동일한 homogeneous coordinates에 속하는 좌표로 변환하면
(5)식 (5)는 다음과 같은 행렬곱으로 표현될 수 있다.
이 때 z'는 x와 y에 무관하다.
모두 동일한 projection plane()에 projection되기 때문이다.
따라서 z"=-zz'로 정의된 z" 역시 x와 y에 무관하다.이를 통해 위 행렬식의 세 번째 행은 (0 0 )로 단순화할 수 있고, 이를 정리하면 다음과 같은 v'식을 얻을 수 있다.
여기서 다음 식에 주목하자.
(6)앞서 우리는 z'의 범위를 [-1,0]으로 설정했는데, 이는 z축의 범위(-f,-n)을 (-1,0)로 변환한 것과 같다.
따라서 식 (6)에 (-f,-1), (-n,0)을 대입하여 풀면
를 얻을 수 있다.다시 A와 D를 와 로 풀어 정리하면 최종 projection matrix를 얻을 수 있다.
LHS / RHS
위의 행렬을 통해 변환된 물체는 여전히 RHS에서 정의되어 있다.
그러나 이후에 수행될 래스터화 단계는 LHS 환경에서 설계되어 있다.
따라서, RHS 좌표계를 LHS 좌표계로 변환해야 한다.
z축 반전z-negation을 통해 이를 수행할 수 있다.
이전 포스트의 Clockwise/Counter-clockwise 부분에서 RHS - LHS 간 포팅을 위해서는 2가지 리모델링이 수행되어야 한다고 설명했다.
1. 삼각형 정렬 순서의 변경
2. z좌표의 부호 변경 (xy 평면에 대한 반사)삼각형 정렬 순서의 변경의 경우, 래스터화 단계의 파라미터 수정 등을 통해 이 작업을 대체할 수 있다.
따라서 projection transform 단계에서는 z좌표의 부호 변경 작업만 수행한다.
위 행렬식에서 z축에 영향을 주는 행은 3번째 행이다.
따라서 3번째 행의 모든 원소의 부호를 변경하면 LHS 좌표계에서의 projection matrix를 구할 수 있을 것이다.
최종적으로 projection transform 단계에서 사용되는 projection matrix 는 다음과 같이 표현될 수 있다.
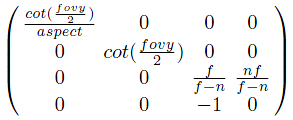
만약 view volume이 2*2*1 크기가 아닌 2*2*2 크기라면 projection matrix는 다음과 같다.
위의 유도 과정의 식 (6)에 ((-f,-1), (-n,0)) 이 아닌, ((-f,-1), (-n,1))을 대입함으로써 얻을 수 있다.