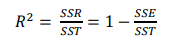▷ 오늘 학습 계획: 통계 강의(심화 3~4)
📖 09_상관분석, 회귀분석
1) 상관분석
상관관계(correlation coefficient)
상관계수 : 두 변수간의 함수 관계가 선형적인 관계가 있는지 파악할 수 있는 측도
상관계수가 0이라는 것은 두 변수 간에 선형 관계가 존재 하지 않는다는 뜻표본상관관계(sample correlation coefficient)
2) 단순 회귀분석
회귀 분석(regression analysis)
변수들간의 함수적 관계를 선형으로 추론하는 통계적 분석 방법
독립변수를 통해 종속변수를 예측하는 방법종속 변수(dependent variable)
다른 변수의 영향을 받는 변수(반응변수), 예측 하고자 하는 변수
독립 변수(independent variable)
종속변수에 영향을 주는 변수(설명변수), 예측 하는 값을 설명해주는 변수
단순 회귀분석(simple regression analysis)
하나의 독립변수로 종속변수를 예측하는 회귀 모형을 만드는 방법
회귀선으로부터 각 관측치의 오차를 최소로하는 선을 찾는 것이 핵심
- 최소제곱법(method of least squares)
정규성 가정, 등분산성 가정, 독립성 가정
최소 제곱법을 통해 구한 추정량: 최소제곱추정량(LSE)
최소제곱법을 통해 회귀모형의 모수를 추정하는 것: OLS(Ordinary
Least Square)
분산분석표
분산분석을 통해서 회귀식의 유의성을 판단 할 수 있음
SST(총제곱합) = SSE(잔차제곱합) + SSR (회귀제곱합)
자유도: (n – 1) = (n -2) + 1결정 계수(Coefficient of determination)
추정된 회귀식이 얼마나 전체 데이터에 대해서 적합한지(설명력이 있는지)를 수치로 제공하는 값(0과 1사이에 값으로 1에 가까울수록 추정된 모형이 설명력이 높다고 할 수 있음)
수정 결정 계수
결정 계수는 유의하지 않은 변수가 추가되어도 항상 증가된다.
수정 결정 계수는 특정 계수를 곱해 줌으로써 항상 증가하지 않도록 함
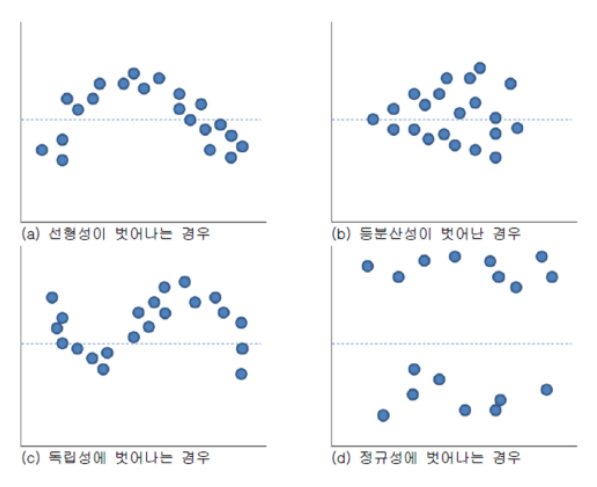
보통 모형 간의 성능을 비교할 때 사용함잔차 분석
(a) 종속변수와 독립변수가 선형 관계가 아님
(b) 일반적인 회귀모형 사용 불가
(c) 시계열 데이터 또는 관측 순서에 영향을 받으면 Durbin-Watson test 실행
(d) 잔차가 -2와 2사이에 분포해야 함, Normal Q-Q plot으로도 확인
3) 다중 회귀분석
다중 회귀분석(multiple regression analysis)
2개 이상의 독립변수로 종속 변수를 예측하는 회귀 모형을 만드는 방법
로지스틱 회귀분석(Logistic regression analysis)
반응 변수가 범주형(이진수)인 경우 사용하는 모형
다항 회귀분석(polynomial regression)
독립 변수가 k개이고 반응 변수와 독립변수가 1차 함수 이상인 회귀 분석
변수선택법
전진선택법(forward selection)
후진 제거법(backward selection)
단계접 방법(stepwise selection)더미 변수(dummy variable)
값이 ‘0‘ 또는 ‘1’로 이루어진 변수
다중공선성(Multicollinearity)
상관관계가 높은 독립변수들이 동시에 사용될 때 문제가 발생
결정계수 값은 높아 회귀식의 설명력은 높지만 독립변수의 P-value 커서 개별 인자들이 유의하지 않는 경우
일반적으로 분상팽창요인 (Variance Inflation Factor: VIF)이 10 이상이면 다중공선성이 존재함
▷ 내일 학습 계획: 통계 강의(심화 5~6)