Improving Visual Grounding by Encouraging Consistent Gradient-based Explanations

Abstract, Introduction

해당 논문은 VLM에서 gradient 텍스트기반의 attention map을 사용한 학습방법과 attention mask consistency objective function을 소개한다. 이는 사람이 지정한 이미지의 특정 영역과 더 잘 맞도록 학습하는 방식이다. 이는 이미지 내 문구를 더 정확하게 찾아낼 수 있으며 제한된 양의 데이터에서 학습할 떄 정확도가 향상된다. 모델은 ALBEF을 사용한다.

문제: '그라운딩(grounding)' 데이터를 포함하는 학습 데이터는 상대적으로 제한적, 이로 인해, 모델이 텍스트와 연결된 이미지의 정확한 영역을 찾는 시각적 그라운딩에서 성능이 떨어지는 문제

본 논문은 marginal-based loss방식을 제안한다. 이는 gradient-based exgrounding 과 localization 능력향상에 초점을 두고 있다. 이 논문은 GradCAM을 이용해 생성된 히트맵을 인간이 제공한 영역 기반 annotation과 일치시키는 새로운 학습 목표(AMC)를 제안. 더 정확한 시각적 그라운딩을 할 수 있도록 유도할 수 있다고 주장함.

저자들의 방식은 ALBEF 모델 보다 좋은 성능을 가진다고 한다. 저자들의 방식이 Flickr30k and RefCOCO+ (둘다 pointing game 벤치마크) 에서 가장 좋은 성능을 가진다고 한다.

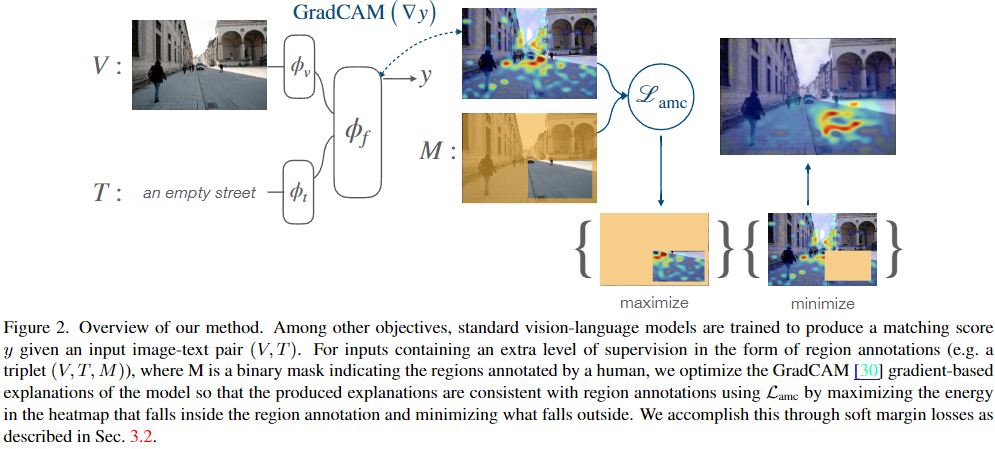
Method

$\phi_{v}$: image encoder, $\phi_{t}$: text encoder, $\phi_{f}$: fusion encoder,
$M$: region annotation,
$H(·, ·)$ is the cross-entropy,
$y$ is a one-hot vector with two entries [y, 1 − y] indicating whether the drawn sample (V, T ) corresponds to a matching image-text pair or not.

input image 가 visual tokens ( $v_{cls}$ )형태로 encoding이 되고 text 또한 sequencial token ( $t_{cls}$ )형태로 encoding이 된 후 [CLS] 로 나눠준다.

Our proposed loss relies on first producing explanation heatmaps or “attention maps” using the GradCAM method.

GradCam Method는 multimodal fusion transformer ( $\phi_{f}$ ) 에서 뽑아낸다.
$F_z = \phi_z (\phi_v (V), \phi_t (T))$ 해당 함수를 $\phi_z$라고 함.

그런 후 $F_z$의 gradient를 계산한다. 이게 matching loss ( $L_{itm}$ )와 같은 형태라고 한다.

$G_z = ∇H (y, \phi_f^{cls} (\phi_v (V), \phi_t (T)))$.

아래는 heatmap $A$를 만드는 과정이다.

$A = ReLU(Fz ⊙ Gz )$

The next step is to leverage the region annotations M so that the model focuses its heatmap scores in A inside the region of interest indicated by M

히트맵에서 사람이 만든 영역 내부의 평균 값이 영역 외부의 평균 값보다 크도록 최대화하는 손실 함수 - 모델이 관심을 두는 영역이 인간이 제공한 주석 영역과 일치하도록 유도

$L_{mean} =E_{(V,T,M )∼D} max(0, \frac{1}{N^c} \sum_{i,j}(1 − M_{i,j} ) A_{i,j}− \frac{1}{N} \sum_{i,j} M_{i,j} A_{i,j} + ∆_1)$

Lmax: 표기된 영역 내부의 최대 히트맵 값이 외부의 최대 값보다 크도록 하는 손실 함수. 이 손실 함수는 모델이 가장 중요한 영역을 정확히 찾도록 한다.
$L_{max} =\mathbb{E}_{(V,T,M )∼D} max(0, max_{i,j}((1 − M_{i,j} ) A_{i,j}) − max_{i,j}( M_{i,j} A_{i,j}) + ∆_2)$

최종수식:

$L_{amc} = λ1 · L_{mean} + λ2 · L_{max},$

Experiment

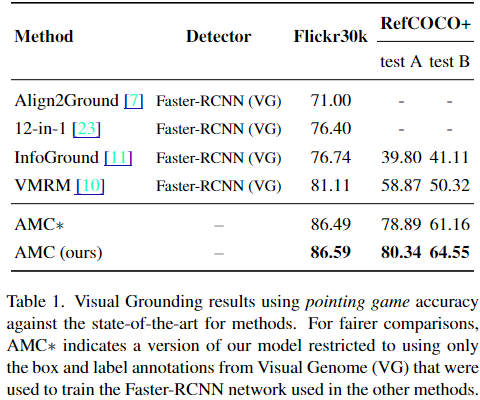
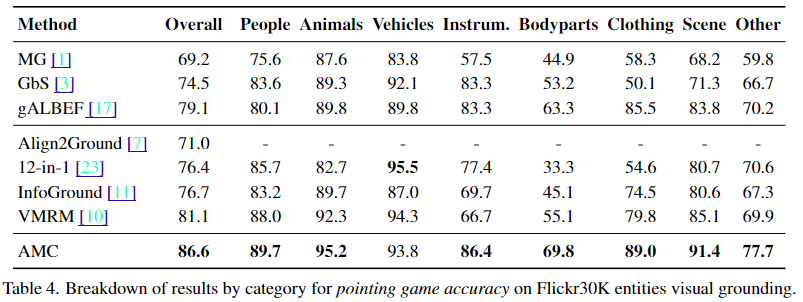
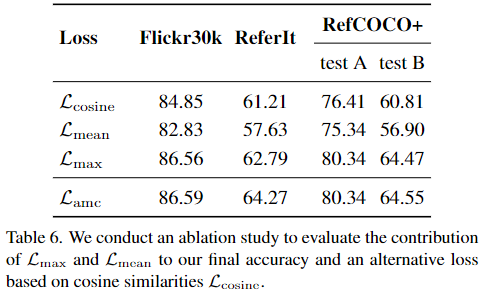
Ablation