ELECTRA : Pre-training Text Encoders as Discriminators Rather Than Generators

요약

Electra 모델은 정확도와 함께 학습의 효율성에 주목한다. 본 논문에서는 학습의 효율 향상을 위해 Replaced Token Detection(RTD)이라는 새로운 pre-training task를 제안했다.

ELETRA모델은 빠르고 효과적으로 학습한다. 동일한 조건에서 BERT의 성능을 능가했으며 small 모델 성능에서는 하나의 GPU를 사용해 단 4일만에 학습한 모델로 계산량이 30배인 GPT를 능가했다. Large모델의 경우 RoBERTa나 XLNet 대비 1/4 계산량 만으로 비슷한 성능을 냈다.

---

Intro

SOTA 학습 방법은 denoising autoencoder 학습방식이다. 입력 시퀀스 15%정도 마스킹하고 이를 복원하는 MLM Task를 통해서 학습을 진행한다. denoising autoencoder방식은 autoregressive language modeling 학습방식에 비해 양방향성을 고려한다는 점이서 효과적인 학습이지만 문제점이 존재

1. 전체 token 중에 15% 에서만 loss 가 발생한다.
2. 그렇기 때문에 학습하는데 비용이 많이든다
3. 학습 때 [MASK] 토큰을 모델이 참고해 예측하지만 실제(inference)에서는 MASK token이 존재하지 않는다.

Method

논문에서는 이러한 문제 해결을 위해 RTD 라는 방식을 새로운 pre-training task 로 제안한다. RTD는 generator(G)를 이용해 실제 입력의 일부 토큰을 그럴싸한 가짜토큰으로 바꾸고, 각 토큰이 실제 입력에 있는 진짜인지 generator에서 생성한 가짜토큰인지 discriminator(D)에서 맞추는 이진분류 문제이다.

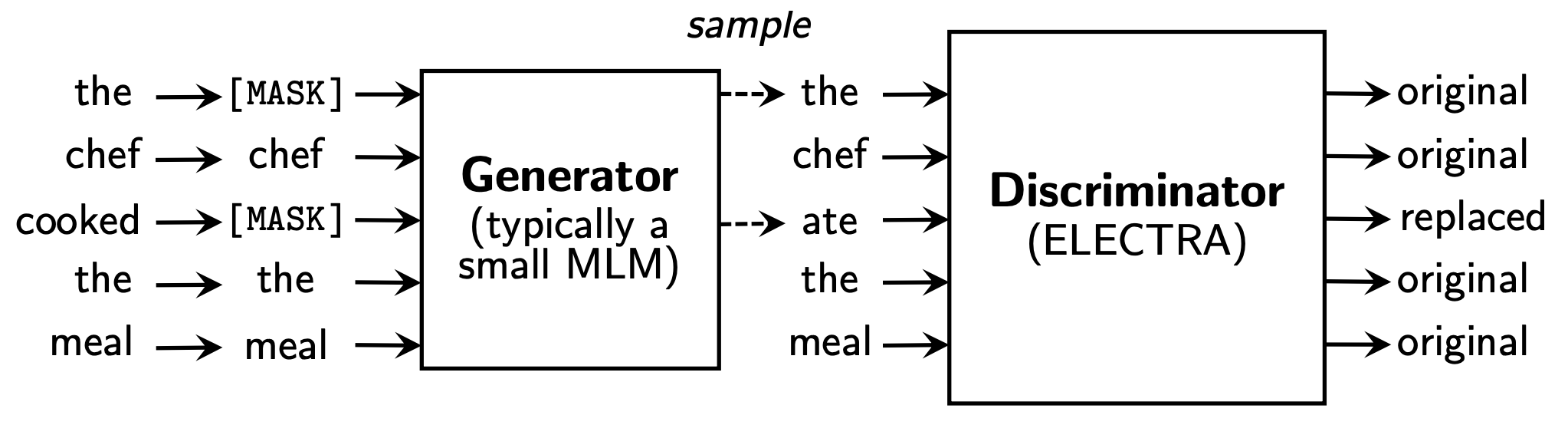
RTD방식은 15%만 학습하는 것이 모든 토큰을 대상으로 학습이 진행되므로 상당히 효율적이며, BERT 보다 훨씬 빠르게 학습할 수 있다.

RTD 학습 방식을 자세히 보면 G, D 두개의 네트워크가 필요하다. 두 네트워크는 공통적으로 Transformer 인코더 구조이며, 토큰 시퀀스는 $x = [x_{1}, x_{2}, … x_{n}]$ 를 입력으로 받아 문맥정보를 반영한 벡터 시퀀스 $h(x) = [h_{1},h_{2}…h_{n}]$ 으로 매핑

Generator

G는 BERT의 MLM과 똑같다. $x = [x_{1}, x_{2}, … x_{n}]$ 에 대해 마스킹할 위치의 집합 $m = [m_{1}, m_{2},…, m_{k}]$을 결정한다.

• 모든 마스킹 위치는 1~n 사이의 정수이고, 수학적으로는 $m_{i} \sim \mathbf{unif} \left \{ 1,n\right\} for i = i ~to~ k$
• 마스킹 개수 : k 는 보통 0.15n을 사용(전체 토큰의 15%)

결정한 위치에 있는 입력 토큰을 MASK로 치환

• $x^{masked} = \mathbf{REPLACE}(x,m,[MASK])$와 같이 표현한다.

마스킹 된 입력 $x^{masked}$에 대해서 G는 아래와 같이 원래 토큰이 무엇인지 예측한다.

• 해당 과정을 수학적으로 표현 ( t 번 째 토큰에 대한 예측) $p_{G}(x_{t}|x^{masked}) = exp(e(x_{t})^{T}h_{G}(x^{masked})_{t})/\sum_{x^{\prime}} exp(e(x^{\prime})^{T}h_{G}(x^{masked})_{t})$
  
• $e(\cdot)$ 은 임베딩을 의미. 위의 식은 LM의 출력 레이어와 임베딩 레이어의 가중치를 공유하겠다는 것을 의미
• 최종적으로 MLM loss 로 학습진행 $\mathcal L _{MLM}(x,\theta {G}) = \mathbb E \left( \sum _{i \in m} - \log p{G}(x{i}|x^{masked})\right)$
  

Discriminator

D는 입력 토큰 시퀀스에 대해 각 토큰이 original 인지 replaced 인지 이진 분류로 학습한다.

G를 이용해 마스킹된 입력 토큰을 예측한다(G 의 loss 학습 전까지)

G에서 마스킹할 위치의 집합 m에 해당하는 위치의 토큰을 $[MASK]$가 아닌 G의 softmax분포 $p_{G}(x_{t}|x)$에 대해 샘플링한 토큰으로 치환(corrupt)한다.

• original input : [the, chef, cooked, the, meal]
• input for G : [ $[MASK]$, chef, $[MASK]$, the, meal]
• input for D : [the, chef, ate, the meal]
• 첫 번째 단어는 샘플링 했을 때 원래 입력과 동일하게 나온 것
• 세 번째 단어는 원래 입력 토큰인 cooked 가 아니고 ate가 나온경우
• $x^{corrupt} = \mathbf {REPLACE}(x,m,\hat{x})$,,, $\hat{x} \sim p_{G}(x_{i}|x^{masked}) ~\mathbf{for} ~i \in m$

치환된 입력 $x^{corrupt}$에 대해서 D는 아래와 같이 각 토큰이 원래 입력과 동일한지 치환된 것인지 예측한다.

• Target class
  • original : 이 위치에 해당하는 토큰은 원본 문장의 토큰과 같은 것
  • replaced : 이 위치에 해당하는 토큰은 G에 의해 변형된 것
• $D(x^{corrupt}, t) = \mathrm{sigmoid}(w^{T}h_{D}(x^{corrupt})_{t})$ → t 번 째 토큰에 대한 예측

최종적으로 아래의 Loss로 학습시킨다.

$L_{Disc}(x,\theta _{D}) = \mathbb{E} \left(\sum_{t=1}^{n} -1 (x_{t}^{corrupt} = x_{t}) \log D(x^{corrupt}, t) -1 (x_{t}^{corrupt} \ne x_{t})\log (1-D(x^{corrupt}, t)) \right)$

GAN과의 차이점

1. 원래 토큰과 동일한 토큰 생성시 GAN은 negative sample( FAKE) 로 간주하지만 ELECTRA에서는 positive sample로 간주한다.
2. G를 D가 속이기 위해 적대적(adversarial)하게 학습하는 것이 아니고 maximum likelihood로 학습한다.
3. G 에 입력으로 노이즈 벡터를 넣지 않는다.

최종적으로 ELECTRA에서 대용량 코퍼스에 대해 G loss 와 D loss의 합을 최소화 하도록 학습한다.

이때 $\lambda$ = 50 으로 사용했다. 이 파라미터는 D loss 와 30000클래스 분류인 G loss 의 스케일을 맞추는 역할을 한다.

$\min_{\theta_{G}, \theta_{D}} \sum_{x \in \mathcal X} \mathcal L_{MLM}(x, \theta_{G}) + \lambda \mathcal L_{Disc}(x,\theta _{D})$

샘플링 과정이 있기 때문에 D loss는 G로는 역전파 되지 않으며, 위 구조로 pre-training을 마친 후 G는 버리고 D만 취해서 downsteam task로 fine-tuning을 진행한다.