소수 판별 알고리즘
소수(Prime Number)란?
1보다 큰 자연수 중 1과 자기 자신을 제외한 자연수로는 나누어 떨어지지 않는 수
소수 판별 알고리즘
# 소수 판별 함수(2이상의 자연수에 대하여)
def is_prime_number(x):
# 2부터 (x - 1)까지의 모든 수를 확인하며
for i in range(2, x):
# x가 해당 수로 나누어떨어진다면
if x % i == 0:
return False # 소수가 아님
return True # 소수임
print(is_prime_number(4)) # 4는 소수가 아님
print(is_prime_number(7)) # 7은 소수임False
True
2부터 X - 1의 모든 자연수에 대하여 연산을 수행하므로 O(X)이다.
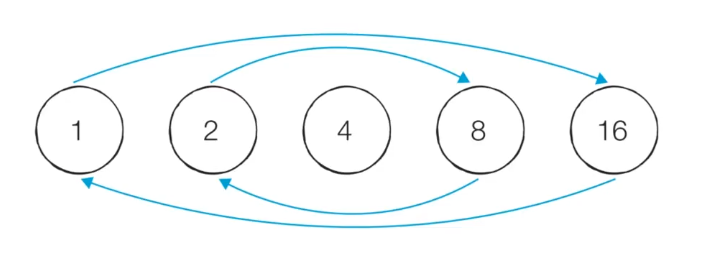
약수의 성질
모든 약수가 가운데 약수를 기준으로 곱셈 연산에 대해서 대칭을 이룬다.
ex) 16의 약수는 1, 2, 4, 8, 16
2 X 8 = 16은 8 X 2= 16과 대칭이다.
특정 자연수의 모든 약수를 찾을 때 가운데 약수(제곱근)까지만 확인하면 된다.
개선된 소수 판별 알고리즘
import math
# 소수 판별 함수
def is_prime_number(x):
# 2부터 x의 제곱근까지의 모든 수를 확인하며
for i in range(2, int(math.sqrt(x)) + 1):
# x가 해당 수로 나누어떨어진다면
if x % i == 0:
return False # 소수가 아님
return True # 소수임
print(is_prime_number(4)) # 4는 소수가 아님
print(is_prime_number(7)) # 7은 소수임False
True
2부터 X의 제곱근까지의 모든 자연수에 대하여 연산을 수행하므로
O(X^1/2)이다.
다수의 소수 판별
특정한 수의 범위 안에 존재하는 모든 소수를 찾아야 할 때는??
=> 에라토스테네스의 체 알고리즘 사용!
에라토스테네스의 체 알고리즘
다수의 자연수에 대하여 소수 여부를 판별할 때 사용하는 대표적인 알고리즘이다.
에라토스테네스의 체는 N보다 작거나 같은 모든 소수를 찾을 때 사용할 수 있다.
- 2부터 𝑁까지의 모든 자연수를 나열한다.
- 남은 수 중에서 아직 처리하지 않은 가장 작은 수 𝑖를 찾는다.
- 남은 수 중에서 i의 배수를 모두 제거한다. (𝑖는 제거하지 않는다.)
- 더 이상 반복할 수 없을 때까지 2번과 3번의 과정을 반복한다.
에라토스테네스의 체 알고리즘 동작 과정
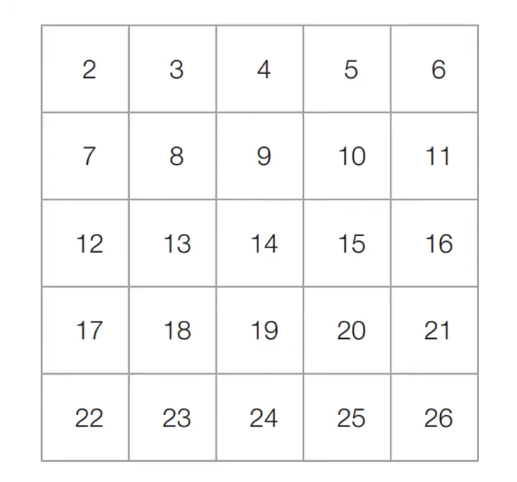
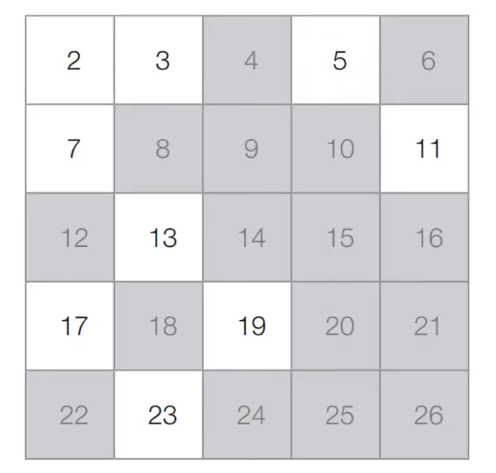
[초기 단계] 2부터 26까지의 모든 자연수를 나열한다.
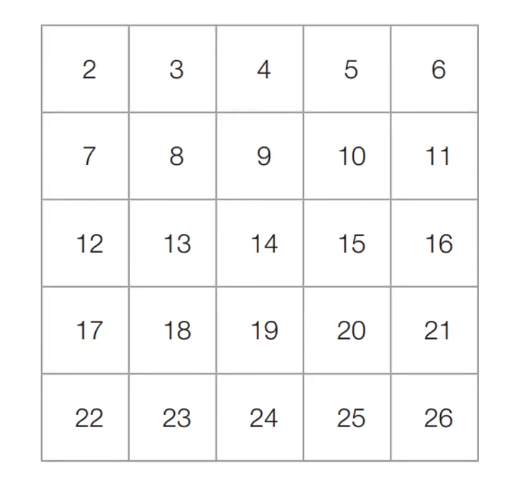
[Step 1] 아직 처리하지 않은 가장 작은 수 2를 제외한 2의 배수를 제거한다.

[Step 2] 아직 처리하지 않은 가장 작은 수 3를 제외한 3의 배수를 제거한다.

[Step 3] 아직 처리하지 않은 가장 작은 수 5를 제외한 5의 배수를 제거한다.
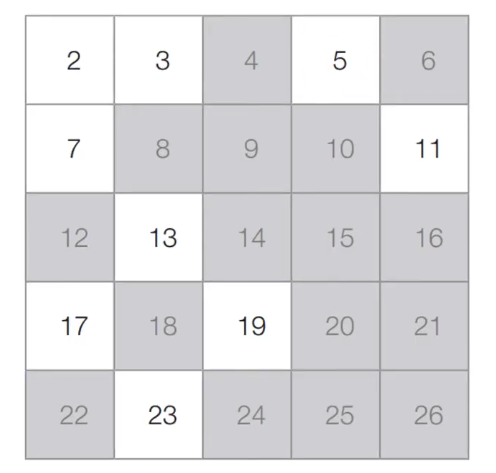
[Step 4] 마찬가지의 과정을 반복하면 아래와 같은 결과를 얻을 수 있다.
에라토스테네스의 체 알고리즘 구현
import math
n = int(input())
array = [True for i in range(n + 1)] # 처음엔 모든 수가 소수(True)인 것으로 초기화
# 에라토스테네스의 체 알고리즘
for i in range(2, int(math.sqrt(n)) + 1): # 2부터 n의 제곱근까지의 모든 수를 확인하며
if array[i] == True: # i가 소수인 경우 (남은 수인 경우)
# i를 제외한 i의 모든 배수를 지우기
j = 2
while i * j <= n:
array[i * j] = False
j += 1
# 모든 소수 출력
for i in range(2, n + 1):
if array[i]:
print(i, end=' ')26
2 3 5 7 11 13 17 19 23
시간복잡도는 O(NloglogN)로 선형 시간에 가까울 정도로 빠르다.
하지만 각 자연수에 대한 소수 여부를 저장해야 하므로 메모리가 많이 필요하다.
투 포인터 알고리즘
투 포인터 알고리즘이란?
리스트에 순차적으로 접근해야 할 때 두 점의 위치를 기록하면서 처리하는 방법
2, 3, 4, 5, 6, 7번 학생을 지목해야 할때 간단히 2번부터 7번까지의 학생이라고 한다.
이와 같이 시작점과 끝점 2개의 점으로 접근할 데이터의 범위를 표현하는 방법이다.
특정한 합을 가지는 부분 연속 수열 찾기
N개의 자연수로 구성된 수열이 있을 때, 합이 M인 부분 연속 수열의 수를 구하라.
(조건 : 시간 복잡도 제한 = O(N))
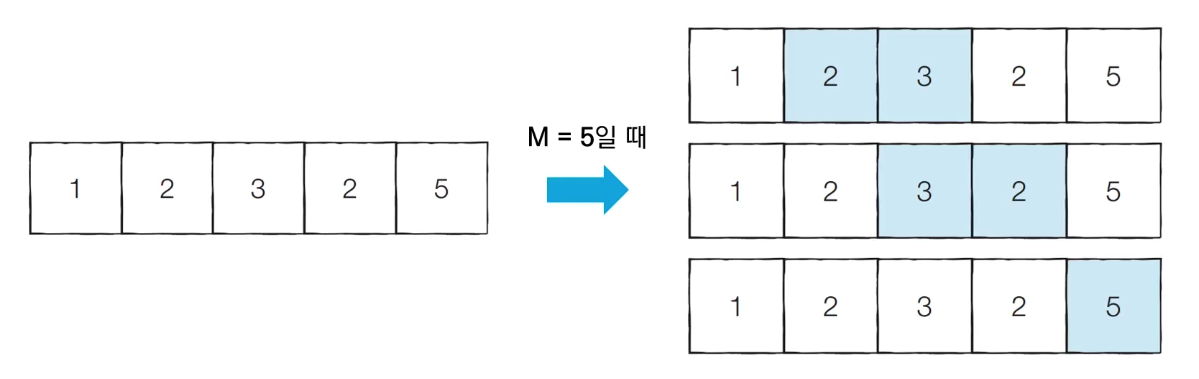
문제 해결 아이디어
투 포인터를 활용하여 다음과 같은 알고리즘으로 문제를 해결할 수 있다.
- 시작점(start)과 끝점(end)이 첫 번째 원소의 인덱스(0)를 가리키도록 한다.
- 현재 부분 합이 M과 같다면, 카운트한다.
- 현재 부분 합이 M보다 작다면, end를 1 증가시킨다.
- 현재 부분 합이 M보다 크거나 같다면, start를 1 증가시킨다.
- 모든 경우를 확인할 때까지 2번부터 4번까지의 과정을 반복한다.
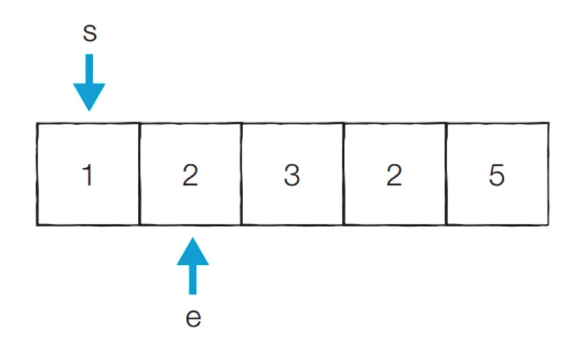
[초기 단계] 시작점과 끝점이 첫 번째 원소의 인덱스를 가리키도록 한다.
현재 부분 합이 1로 5보다 작기 때문에 end가 증가한다.
현재 카운트 = 0

[Step 1] 현재 부분 합이 3으로 5보다 작기 때문에 end가 증가한다.
현재 카운트 = 0
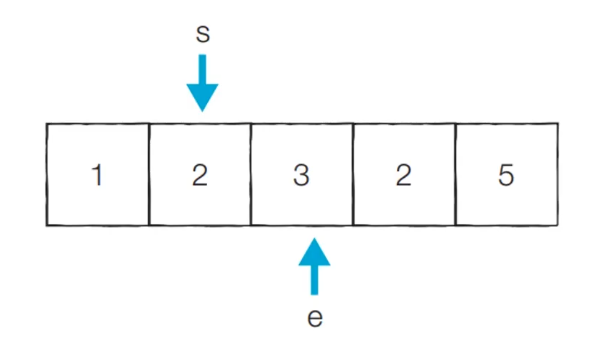
[Step 2] 현재 부분 합이 6으로 5보다 크거나 같기 때문에 start가 증가한다.
현재 카운트 = 0

[Step 3] 현재 부분 합이 5이므로 count가 증가한다.
현재 카운트 = 1
[Step 4] 이전 부분 합이 5로 5보다 크거나 같기 때문에 start가 증가한다.
현재 부분 합이 3으로 5보다 작기 때문에 end가 증가한다.
현재 카운트 = 1
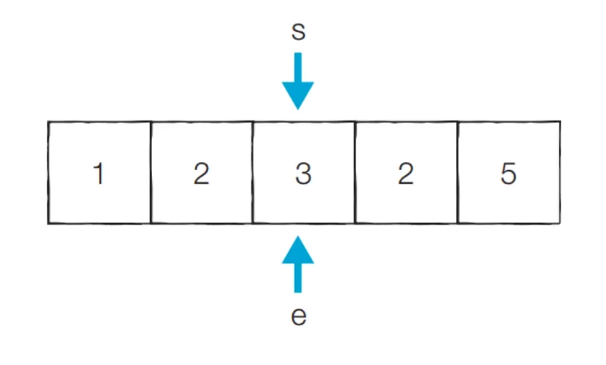
[Step 5] 현재 부분 합이 5이므로 count가 증가한다.
현재 카운트 = 2

[Step 6] 이전 부분 합이 5로 5보다 크거나 같기 때문에 start가 증가한다.
현재 부분 합이 2으로 5보다 작기 때문에 end가 증가한다.
현재 카운트 = 2

[Step 7] 현재 부분 합이 7으로 5보다 크거나 같기 때문에 start가 증가한다.
현재 카운트 = 2
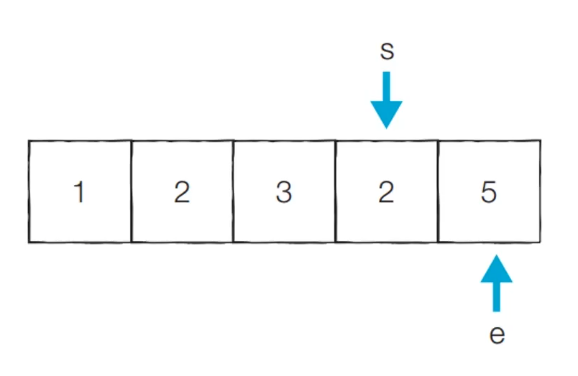
[Step 8] 현재 부분 합이 5이므로 count가 증가한다.
현재 카운트 = 3

특정한 합을 가지는 부분 연속 수열 찾기 알고리즘 구현
n = 5 # 데이터의 개수 N
m = 5 # 찾고자 하는 부분합 M
data = [1, 2, 3, 2, 5] # 전체 수열
count = 0
interval_sum = 0
end = 0
# start를 차례대로 증가시키며 반복
for start in range(n):
# end를 가능한 만큼 이동시키기
while interval_sum < m and end < n:
interval_sum += data[end]
end += 1
# 부분합이 m일 때 카운트 증가
if interval_sum == m:
count += 1
interval_sum -= data[start]
print(count)3
구간 합 빠르게 계산하기
구간 합(Interval Sum)이란?
연속적으로 나열된 N개의 수가 있을 때 특정 구간의 모든 수를 합한 값
구간 합 문제 설명
- 𝑁개의 정수로 구성된 수열이 있다.
- 𝑀개의 쿼리(Query)정보가 주어진다.
1) 각 쿼리는 𝐿𝑒𝑓𝑡와 𝑅𝑖𝑔ℎ𝑡으로 구성된다.
2) 각 쿼리에 대하여 [𝐿𝑒𝑓𝑡,𝑅𝑖𝑔ℎ𝑡] 구간에 포함된 데이터들의 합을 출력해야 한다. - 수행 시간 제한은 O(N + M) 이다.
문제 해결 아이디어
접두사 합(Prefix Sum): 배열의 맨 앞부터 특정 위치까지의 합을 미리 구해 놓은 것
- 𝑁개의 수 위치 각각에 대하여 접두사 합을 계산하여 𝑃에 저장한다.
- 매 𝑀개의 쿼리 정보를 확인할 때 구간 합은 𝑃[𝑅𝑖𝑔ℎ𝑡] - 𝑃[𝐿𝑒𝑓𝑡 - 1]이다.

구간 합 알고리즘 구현
# 데이터의 개수 N과 전체 데이터 선언
n = 5
data = [10, 20, 30, 40, 50]
# 접두사 합(Prefix Sum) 배열 계산 (누적합)
sum_value = 0
prefix_sum = [0]
for i in data:
sum_value += i
prefix_sum.append(sum_value)
# 구간 합 계산 (세 번째 수부터 네 번째 수까지)
left = 3
right = 4
print(prefix_sum[right] - prefix_sum[left - 1])70
참고자료
이코테 2021 강의 9편
이것이 코딩 테스다 교재
