imos 알고리즘
누적합 문제를 효율적으로 풀 수 있는 imos 알고리즘
imos법 사용
imos 법은 아래 예시에서 쓸 수 있는 간단한 아이디어이다.
가게에 Q명의 손님이 방문한다. 가게는 시간 0부터 T까지 운영한다. 각각의 손님 i에 대해 입장 시각 s와 e (1<=s<e<=T)가 주어진다. 가게 운영 중 손님이 가장 많이 방문했을 때의 손님 수는 몇명인가 ? (단, 동일 시각에 입장과 퇴장이 같이 발생할 경우, 퇴장이 먼저 이루어진다고 가정한다.)

각 선분을 손님이 가게에 있던 시간으로 생각한다면, 시간 5에서 손님이 4명으로 가장 많다.
그냥 있는 그대로, 완탐으로 푼다면 cnt 배열에 매번 +1을 해준다.
그렇게 처리하게 되면, 한 사람당 O(T)시간이므로 시간 복잡도 상 매우 안 좋다.
변화 시작과 변화 종료만 기록
더 빠르게 풀 수 있다.
imos법의 기본 아이디어는 변화 시작과 변화 종료반 기록한다로 요약할 수 있다. 말 그대로 각 손님이 입장해서 퇴장하기까지 존재하는 모든 시각에 1을 더하는 것이 아니고, 입장할 때 +1을 기록하고, 퇴장할 때 -1을 기록해서 모든 입력을 처리하고 나서 답을 구하기 전에 누적합을 통한 후처리로 하나만 거치면 된다.
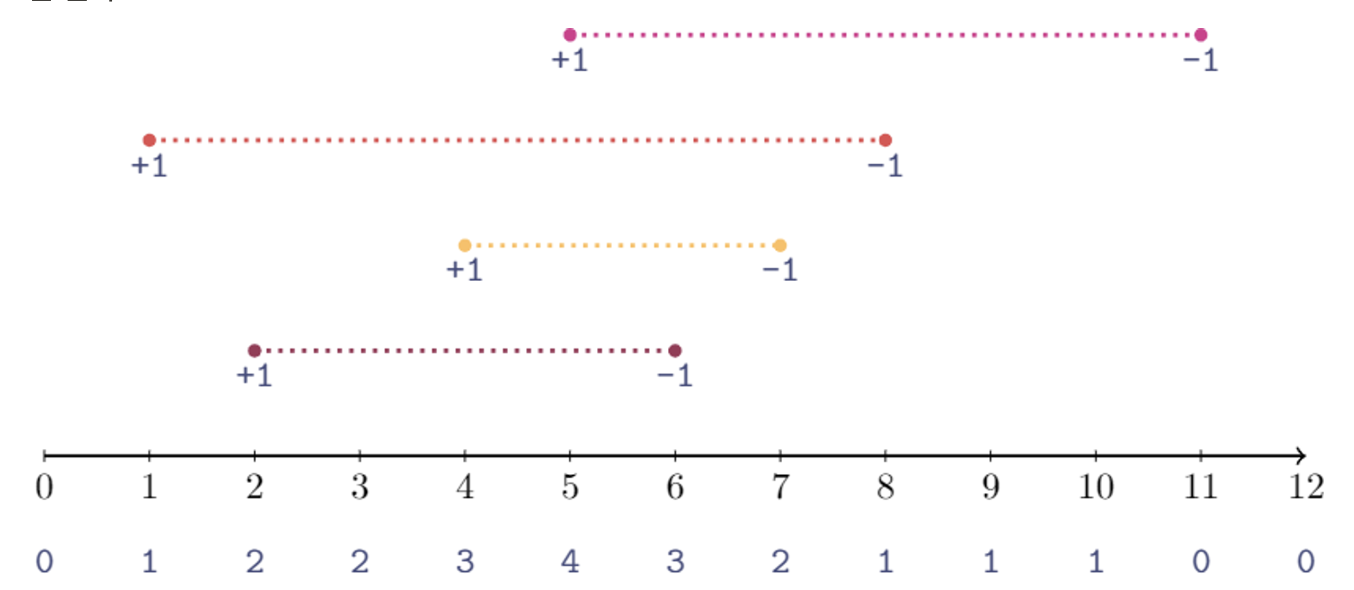
결국 맨 마지막에 +1,-1이 기록된 배열의 누적합(Prefix Sum)배열을 구하면, 원래 구하려던 값이 나오는 것이다.
2차원에서의 imos법
격자 보드에 사각형 그리기
imos법은 특성상 고차원으로 확장이 용이하다.
만약 있는 그대로 계산한다면, 2차원에서의 누적합 역시 매번 더해주는 과정 반복.
가로로 한번, 세로로 한번 휩쓸기
사각형으로 바뀌어도 기본적인 아이디어는 같다. 시작과 끝만 기록한다. 단, 2차원에서는 차원이 늘어난 만큼, 가로 방향으로 시작과 끝, 세로 방향으로 시작과 끝 두 번 기록하고, 누적합 계산 역시 가로로 한번, 세로로 한번 휩쓸면 된다.
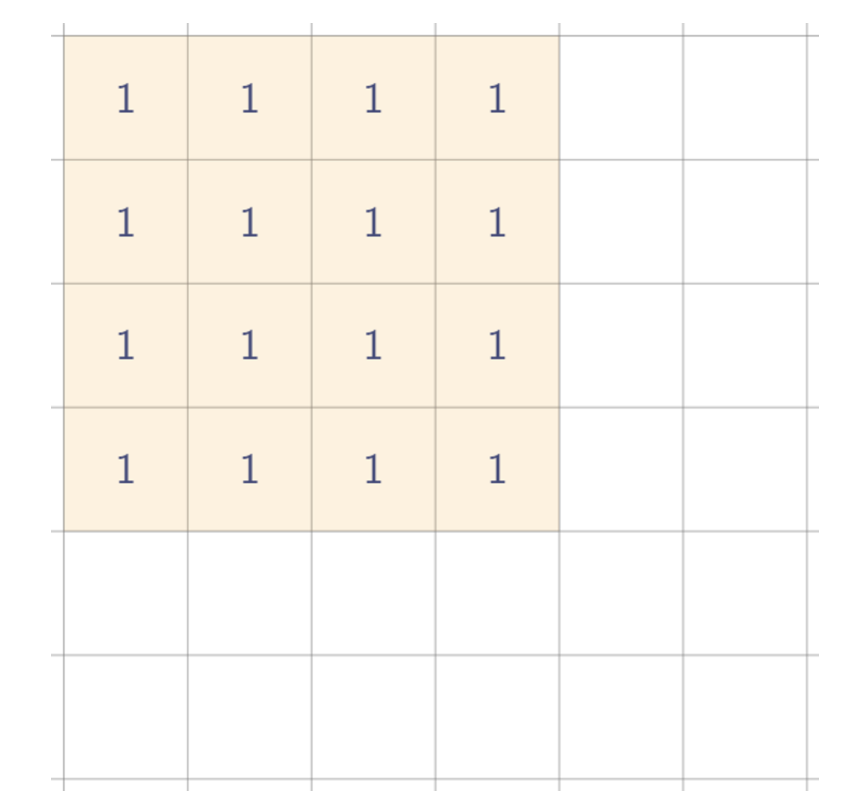
위 예시처럼 되려면
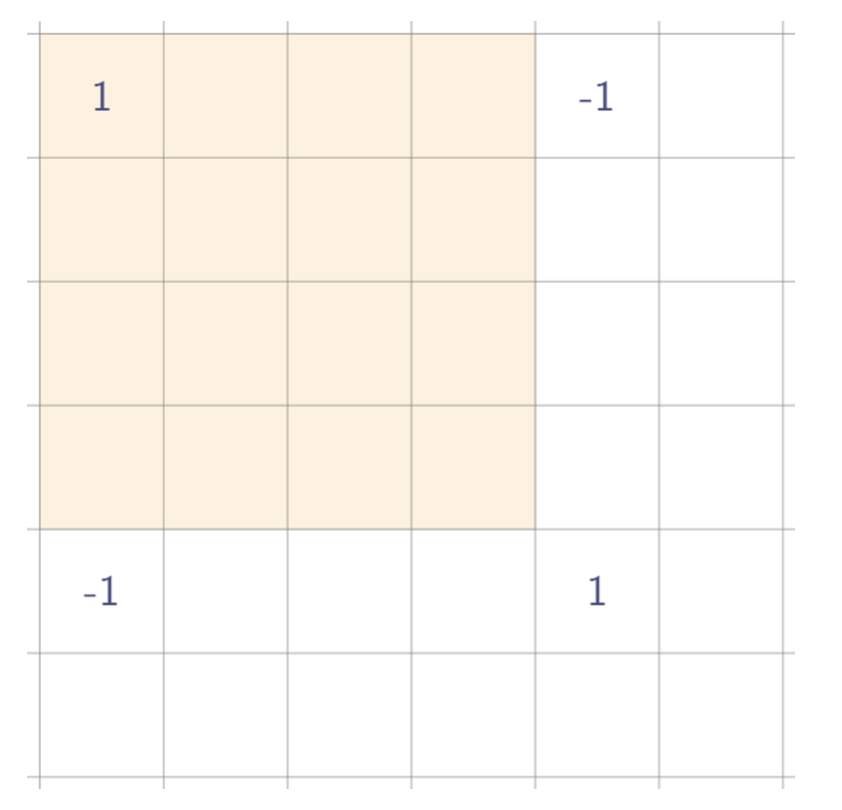
이런 식이면 된다.
즉, 위와 같이 네 개를 찍어두기만 하면, 누적합을 통해 그 위의 사진처럼 가능하다.
- 가로 방향으로 누적합
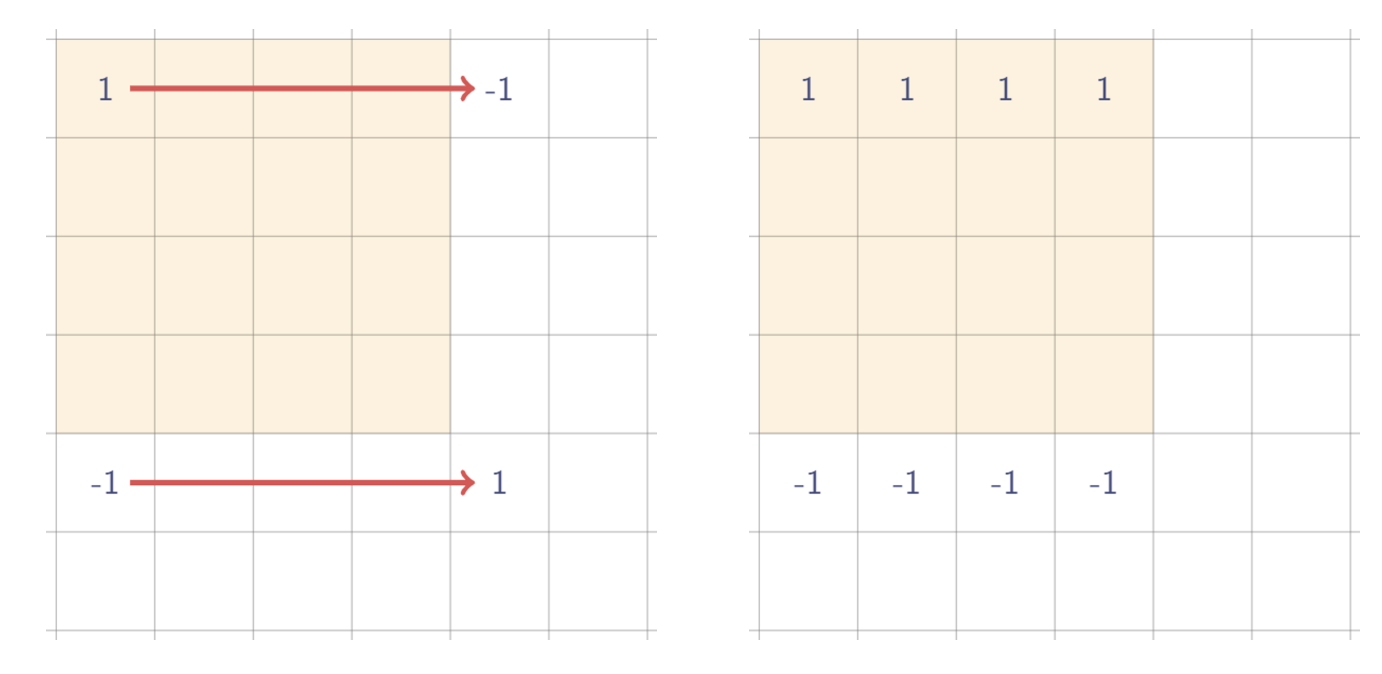
- 세로 방향으로 누적합
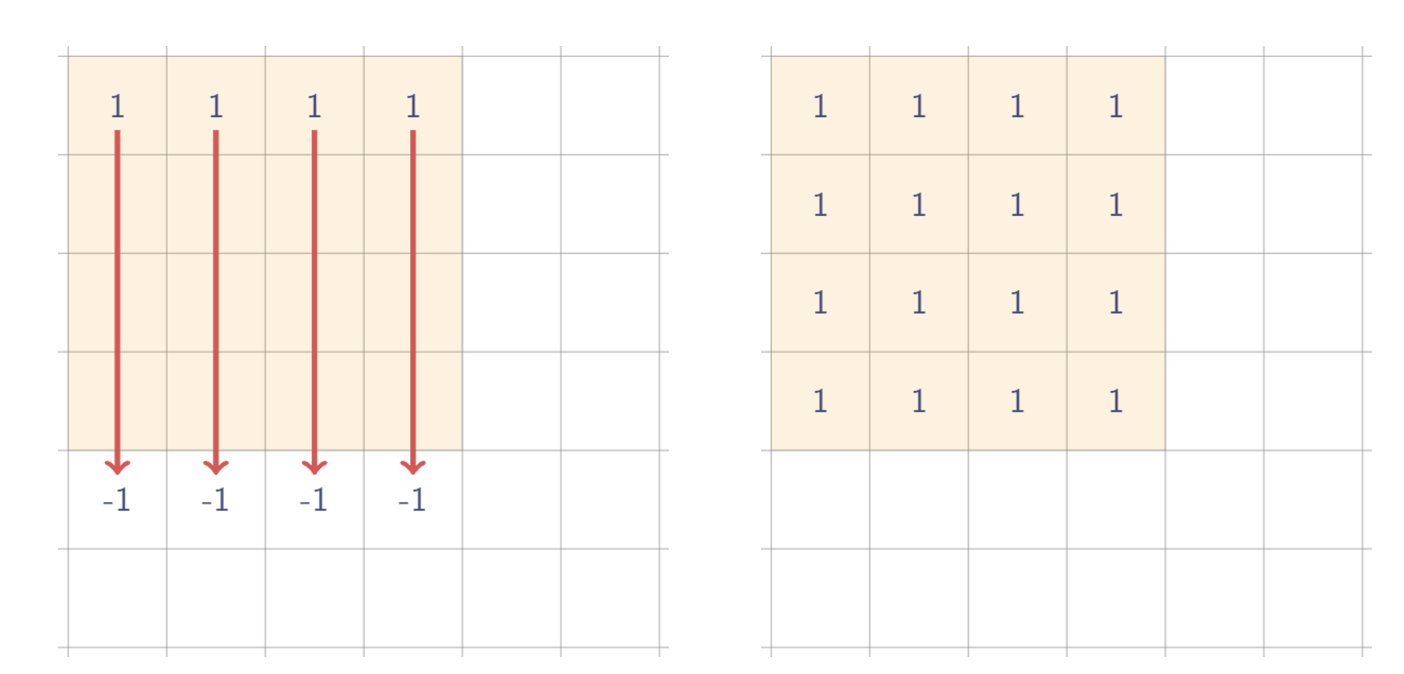
계속 말하지만, 각 사각형들에 대해 실제로 1을 모두 찍는게 아니고, 값 4개만 제대로 찍어두고 나중에 두번 누적합 하면 된다.
정리
imos 알고리즘 주요 특징
- 구간 업데이트 효율적 처리
- 차분 배열을 사용
- 구간의 시작점에 값을 더하고, 끝점 다음에 값을 뺀다.
- 최종 결과는 차분 배열의 누적합으로 얻는다.
구간의 시작점(s)에 +1, 끝점 다음(e+1)에 -1을 적용했따.
모든 구간 처리 후, 누적 합을 계산하여 각 위치의 최종값을 얻는다.
-> 특정 값의 개수를 효율적으로 카운팅하는데 매우 유용하다.
구간 쿼리:
여러 구간에 대한 연산을 한 번에 처리할 수 있다.
예: "구간 [a, b]에 있는 모든 원소에 1을 더하라"와 같은 쿼리를 O(1) 시간에 적용할 수 있다.
중첩된 구간의 카운팅:
여러 구간이 겹치는 경우, 각 지점에서 얼마나 많은 구간이 겹치는지 쉽게 계산할 수 있다.
누적 효과 계산:
각 지점에서의 누적된 효과(예: 총 사용 횟수, 총 변화량 등)를 O(N) 시간에 계산할 수 있다.
대규모 데이터 처리:
데이터의 범위가 매우 클 때(예: 10^9)도 실제 사용되는 지점만 효율적으로 처리할 수 있다.
시간 복잡도 개선:
단순한 방법으로는 O(N^2) 시간이 걸릴 수 있는 연산을 O(N) 또는 O(N log N)으로 개선할 수 있다.
이 알고리즘의 핵심은 변화만을 기록하고, 나중에 한 번의 순회로 모든 결과를 계산한다는 것이다. 이는 많은 구간 기반 문제나, 카운팅 문제에서 시간복잡도를 개선할 수 있다.
따라서 단순히 개수 세는 것을 넘어, 복잡한 구간 기반 연산을 효율적으로 수행할 수 있게 해주는 알고리즘이다 !!