Lower bound & Upper bound

Lower bound와 Upper bound는 이진 탐색의 변형으로, 정렬된 배열에서 특정값을 효율적으로 찾는데 사용된다.

-> 즉, 경계값을 찾는 알고리즘이다. 이진탐색을 기반으로 하기 때문에 정렬되어 있어야 한다.
이진탐색을 기반으로 하기 때문에, 두 알고리즘의 시간 복잡도는 O(logN)이다.

Lower bound

정의 : 주어진 값 이상인 첫번째 원소의 위치를 반환.

• ex) [1,3,3,5,7]에서 값3의 lower bound는 인덱스 1

upper bound

정의 : 주어진 값보다 큰 첫번째 원소의 위치를 반환

• ex) [1,3,3,5,7]에서 값3의 upper bound는 인덱스 3

Lower bound

Lower bound는 특정 값의 시작위치를 찾는 알고리즘이다.

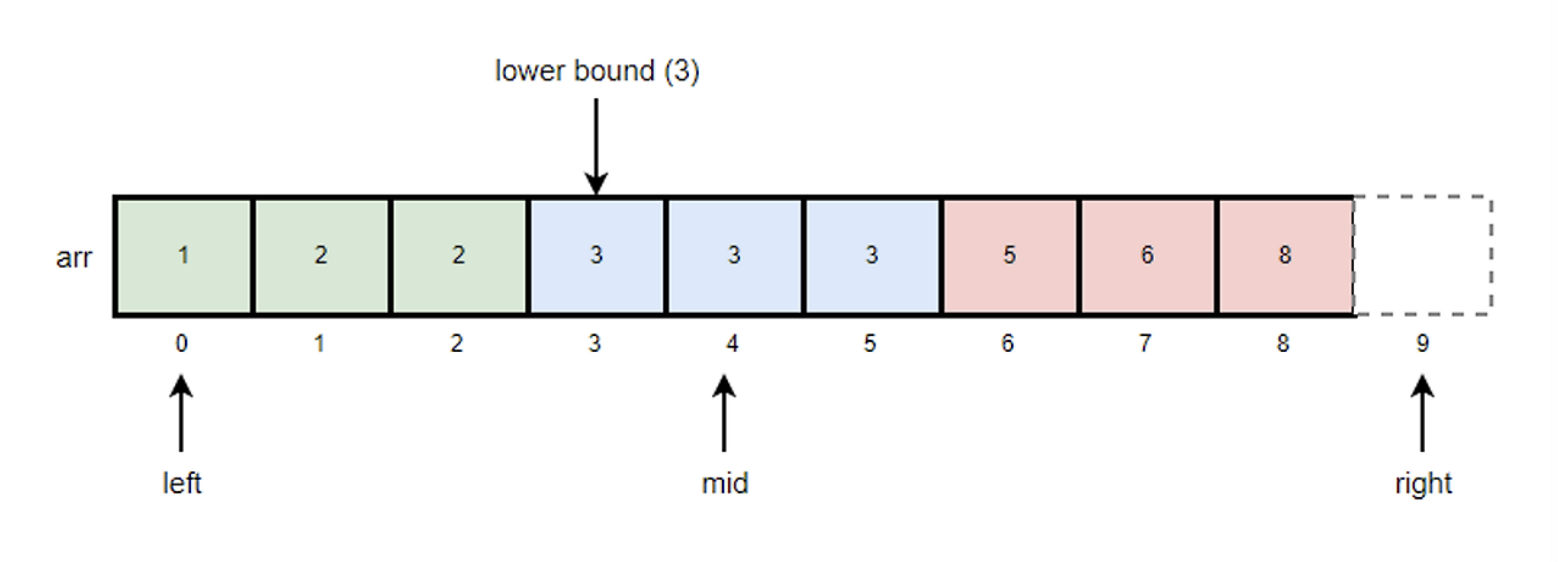
동작 방식

초기에 left는 배열의 시작위치로 right는 배열의 길이로 세팅한다.
1. 배열의 중간값(mid)를 가져온다.
2. 중간 값과 검색 값을 비교한다.

• 중간 값이 검색 값보다 작다면 left 값을 mid + 1로 한다.
• 중간 값이 검색 값보다 크거나 같다면 right값을 mid로 한다.

3. left >= right일 때까지 1번과 2번을 반복한다.
4. 반복이 끝나면 right값이 lower bound가 된다.

예시

arr배열에서 k=3의 lower bound를 찾는 과정

1. mid값을 구하고 k값과 비교한다.

• mid = (left + right) / 2 = (0+9)/2 = 4

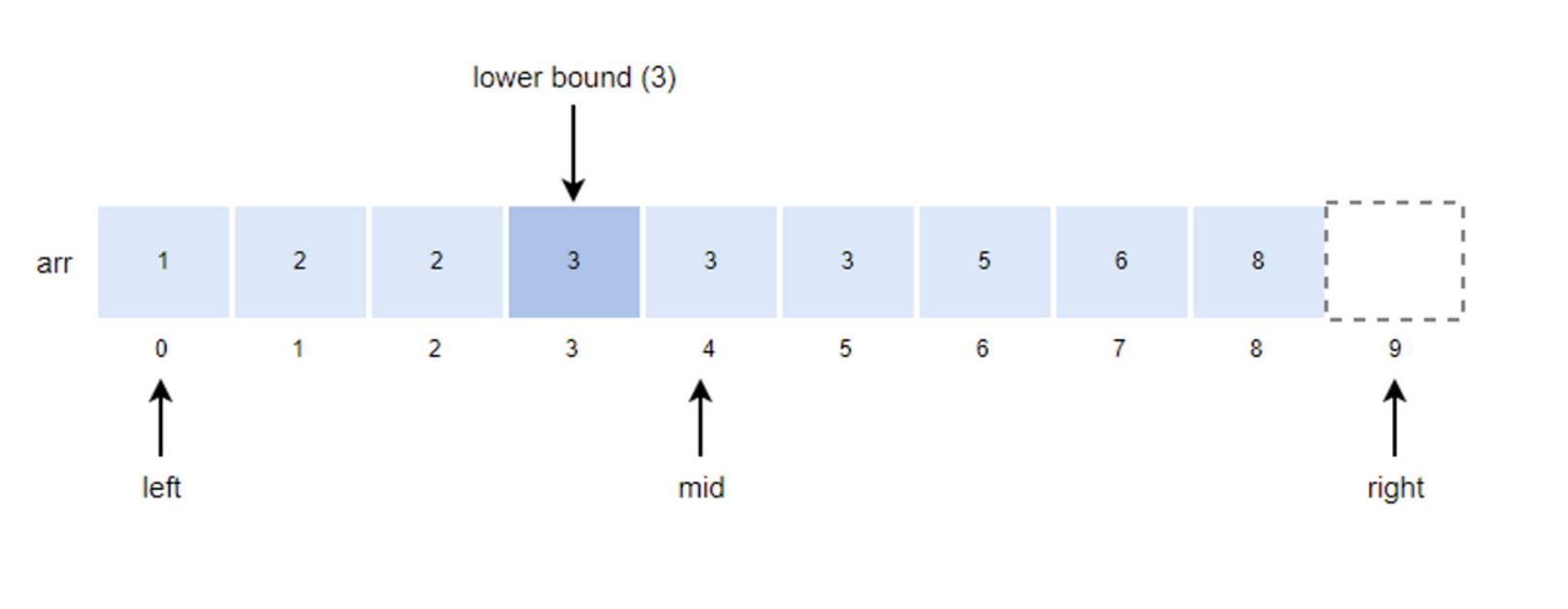
2. k값이 arr[mid]값과 같기 때문에 right의 위치를 mid로 변경한다.

• right = mid = 4

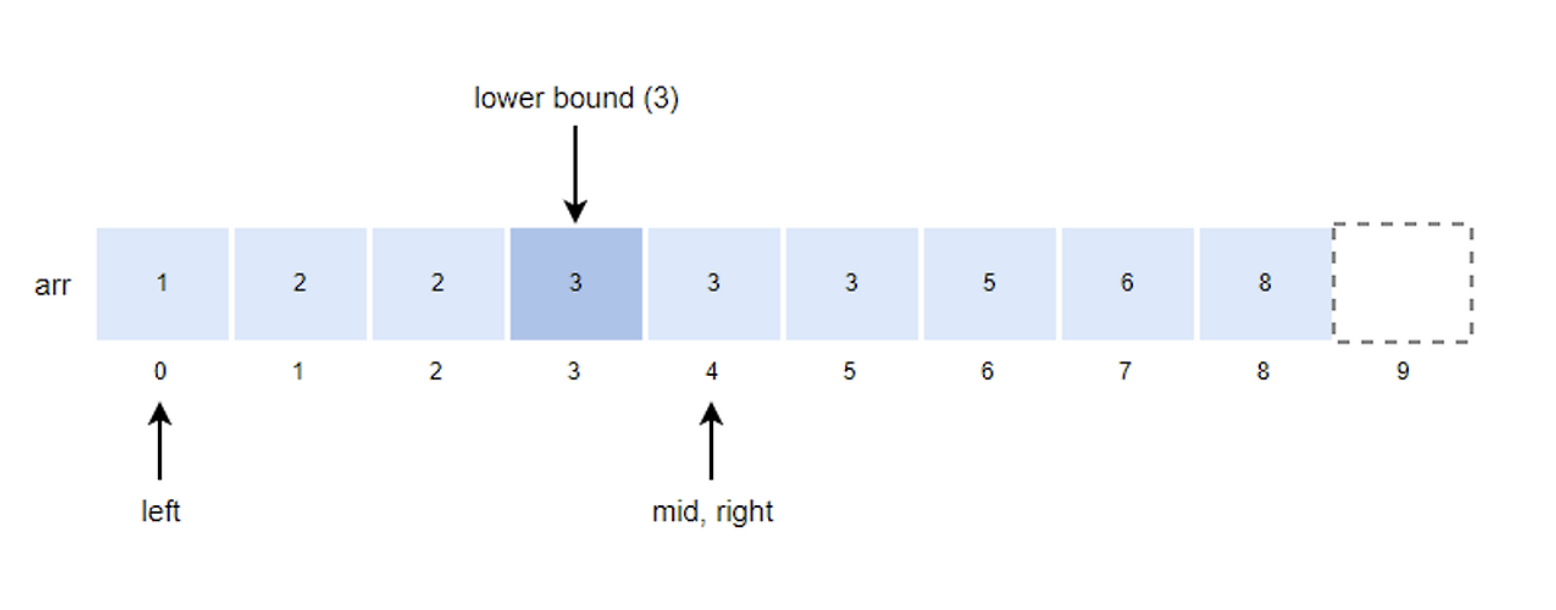
3. mid값을 구하고 k값과 비교한다.

• mid = (left + right) / 2 = (0+4)/2 = 2

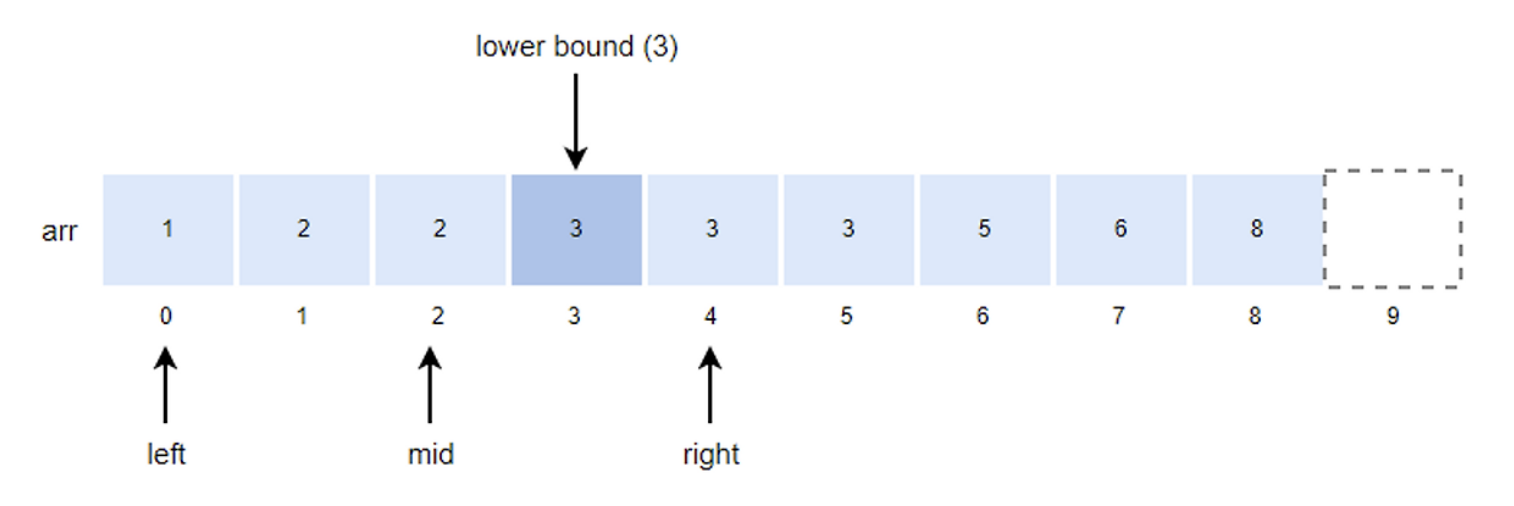
4. k값이 arr[mid]값보다 크기 때문에 left 위치를 mid + 1로 변경한다.

• left = mid + 1 = 3
  

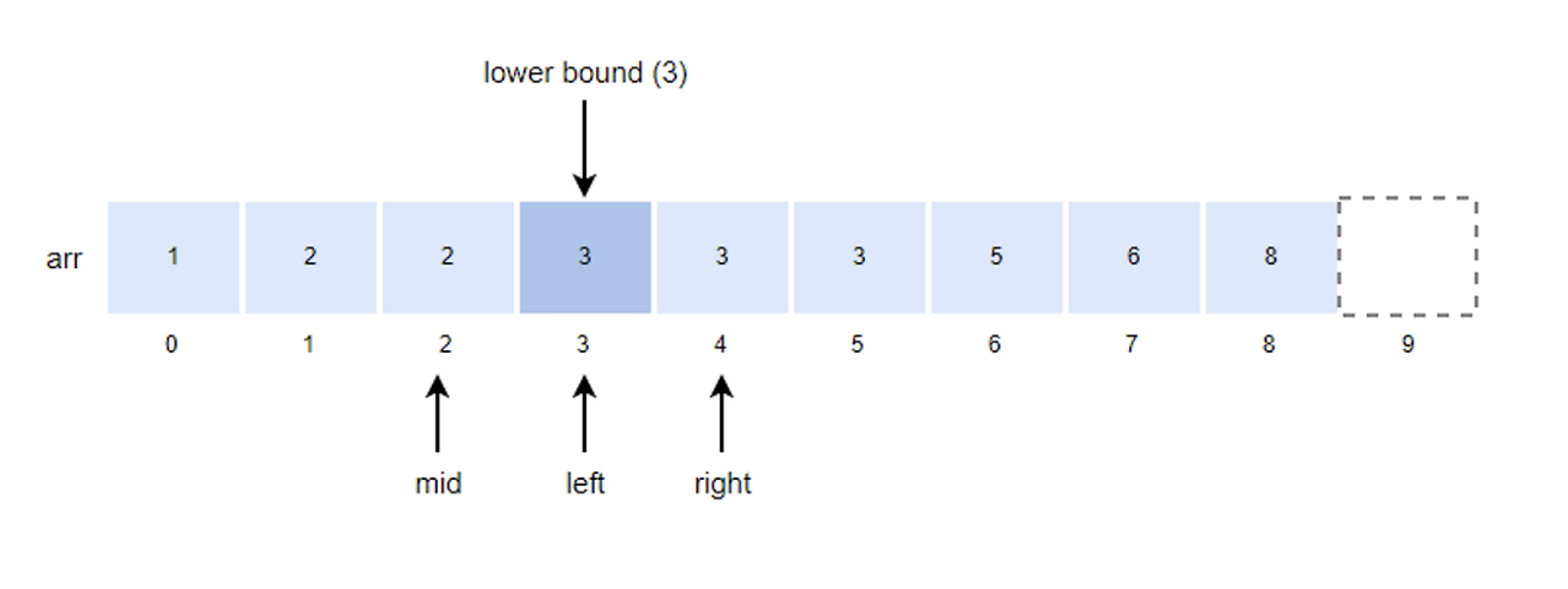
5. mid값을 구하고 k값과 비교한다.

• mid = (left+right)/2 = (3+3)/2 = 3
  

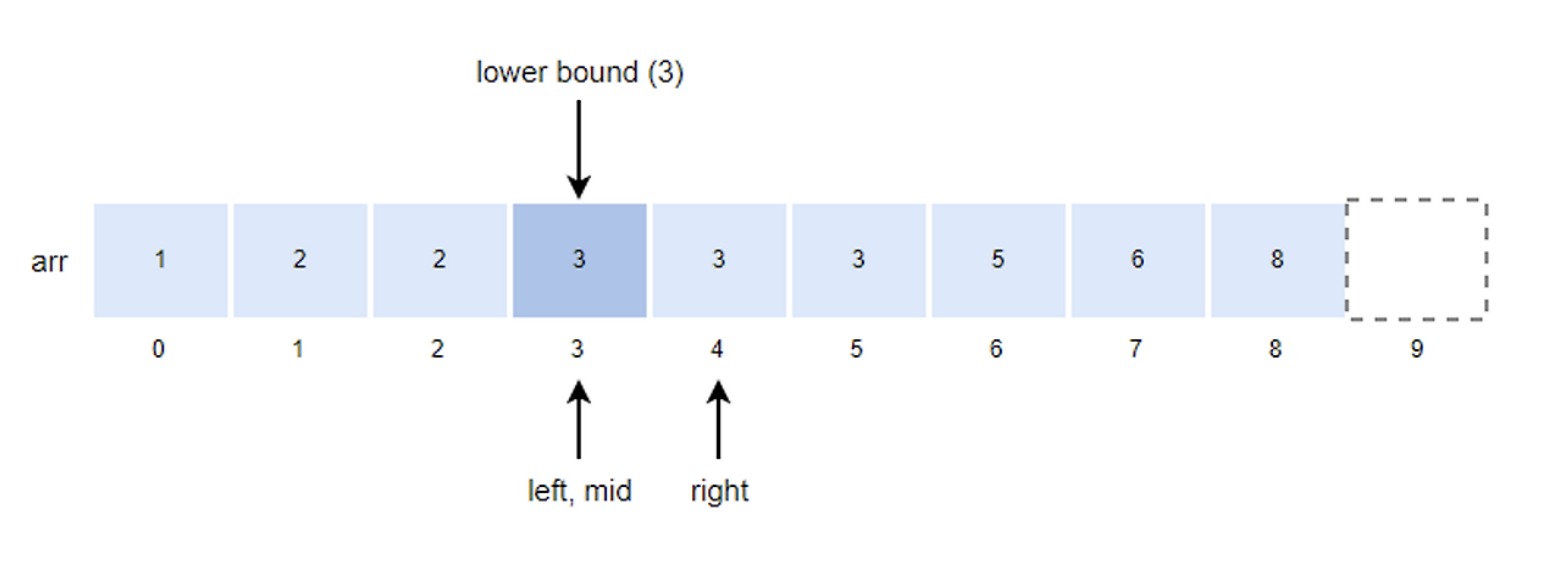
6. k값이 arr[mid]값과 같기 때문에 right 위치를 mid로 변경한다.

• right = mid = 3
• left값이 right값과 같기 때문에 루프를 종료하고 right 값이 lower bound값이 된다.

구현

arr배열에서 k값의 lower bound를 찾는 코드

• 매개 변수로 left는 배열의 시작위치, right는 arr의 길이를 받는다.

def lower_bound(arr, left, right, k):
	while left < right:
		mid = (left + right)//2
		if arr[mid] < k:
			left = mid + 1
		else:
			right = mid

	return right

정확히 일치하는 값이 없더라도, 찾고자 하는 값(k)이상인 첫번째 원소의 위치를 반환한다.

---

Upper bound

Upper Bound는 특정 K값보다 처음으로 큰 값의 위치를 찾는 알고리즘이다.

동작 방식

Upper Bound의 동작 방식...

초기에 left는 배열의 시작위치, right는 배열의 길이로 세팅한다.
1. 배열의 중간값(mid)를 가져온다.
2. 중간 값과 검색값을 비교한다.

• 중간값이 검색값보다 작거나 같다면 left값을 mid + 1로 한다.
• 중간값이 검색값보다 크다면 right값을 mid로 한다.

3. left >= right일때까지 1번과 2번 반복한다.
4. 반복이 끝나면 right 값이 upper bound가 된다.

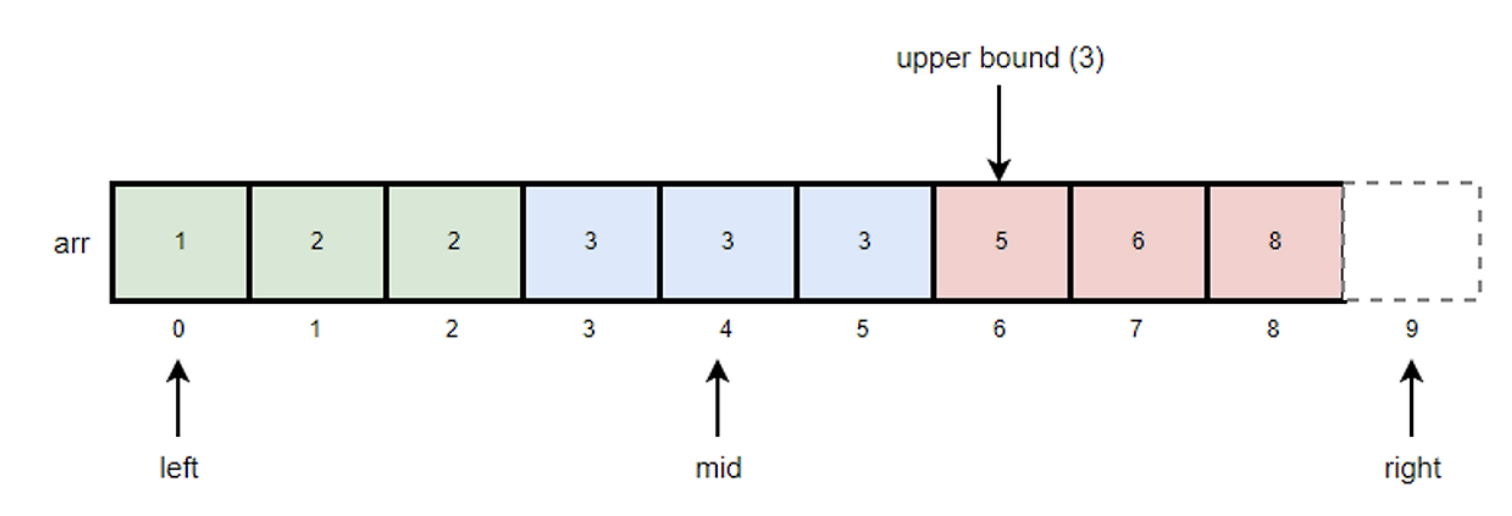
arr배열에서 k=3의 upper bound를 찾는 과정

1. mid값을 구하고 k값과 비교한다.

• mid = (left + right)/2 = (0+9)/2 = 4
  

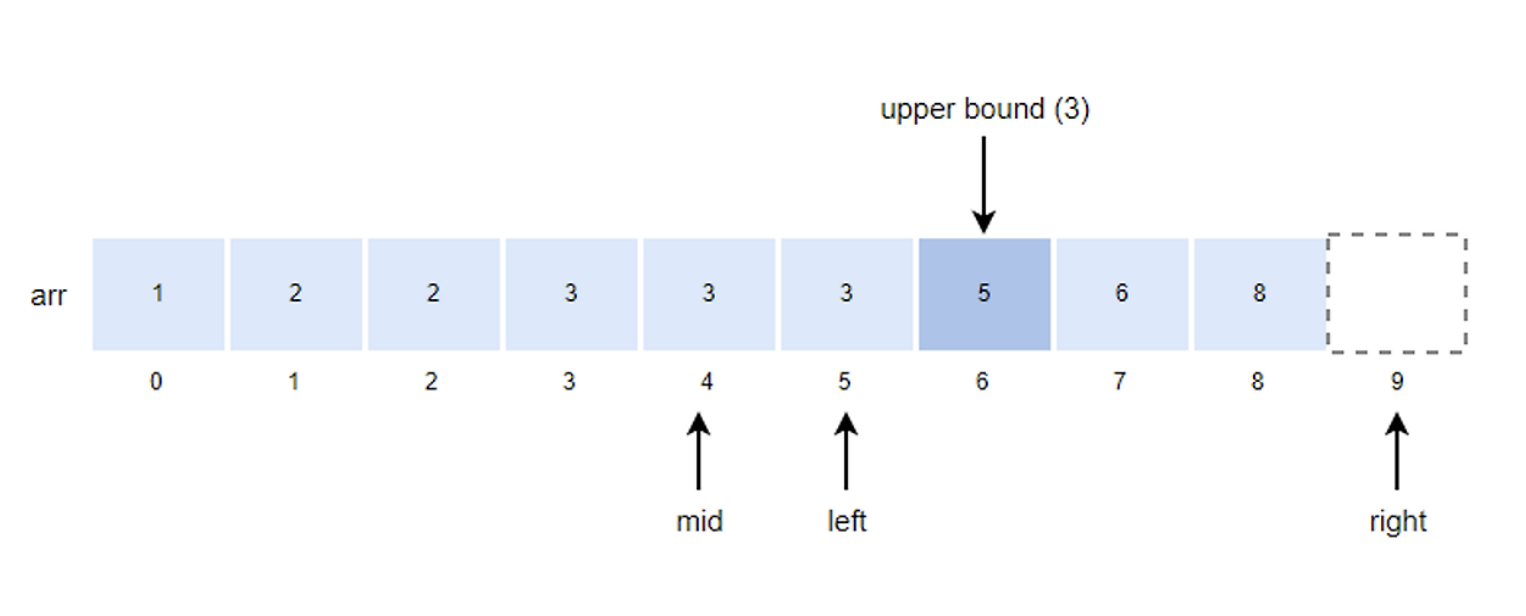
2. k값이 arr[mid]값과 같기 때문에 left위치를 mid + 1로 변경한다.

• left = mid + 1 = 4 + 1 = 5
  

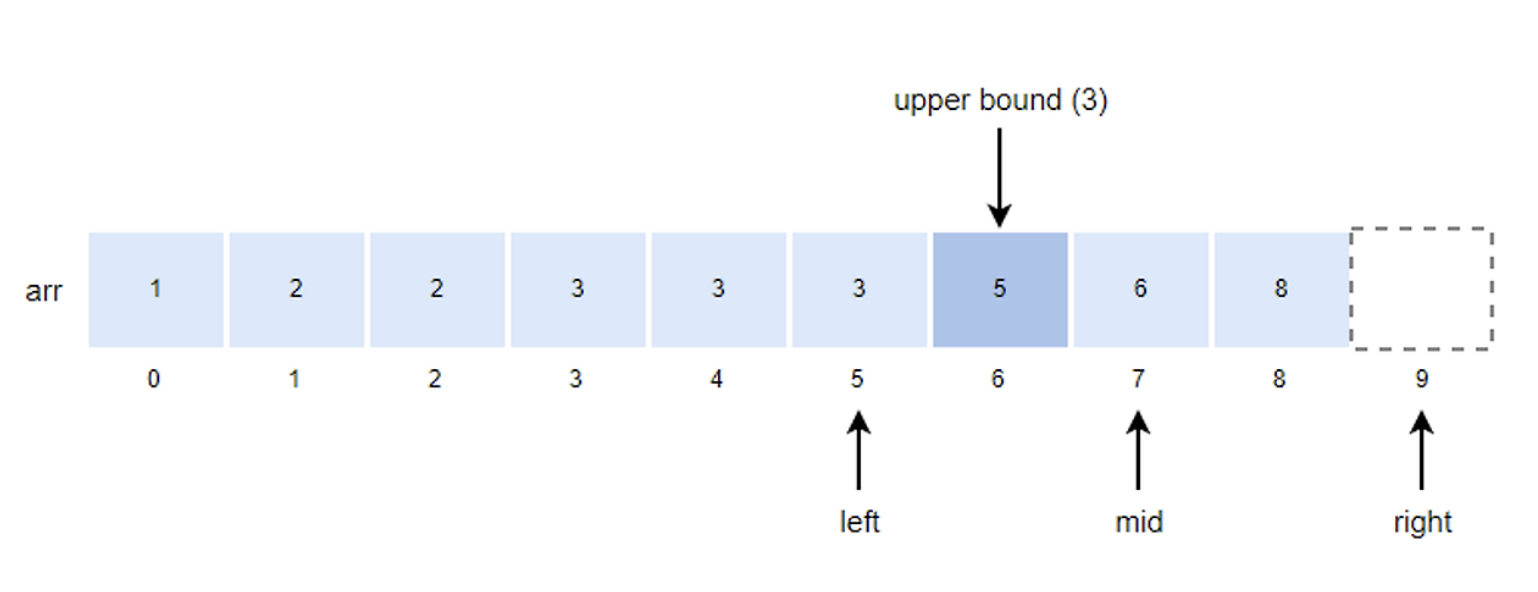
3. mid값을 구하고 k값과 비교한다.

• mid = (left + right) / 2 = (5+9)/2 = 7
  

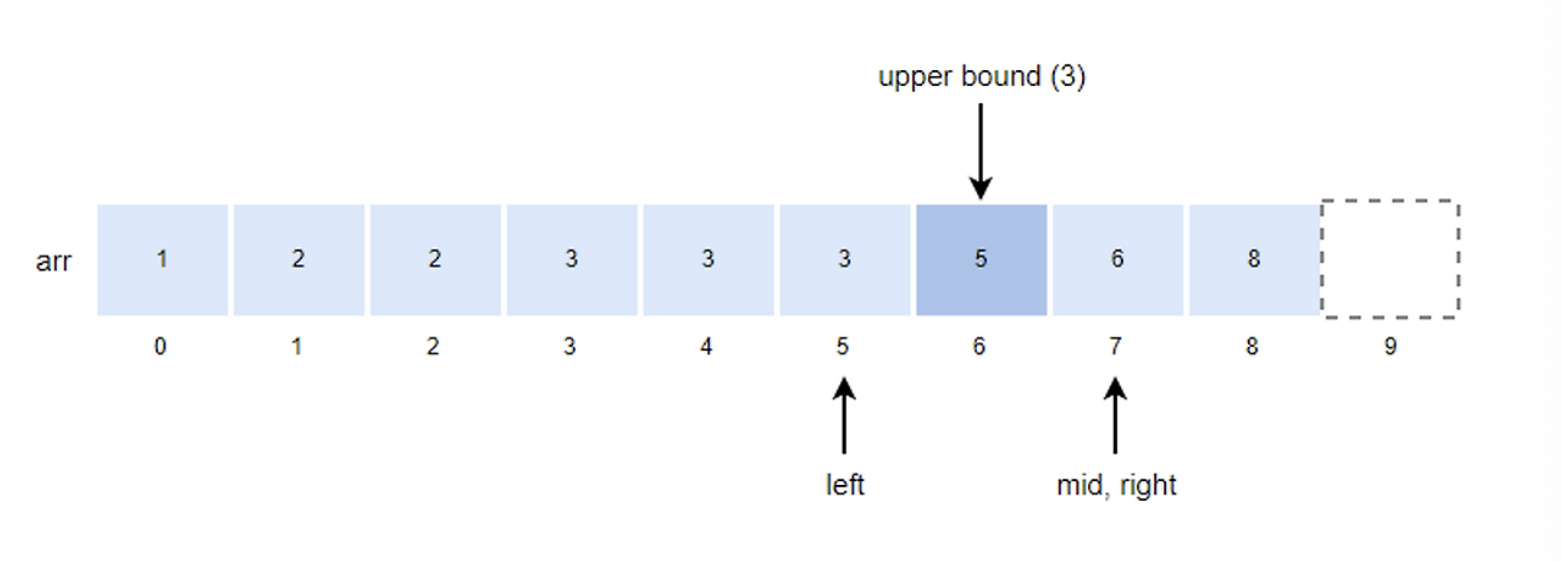
4. k값이 arr[mid]값보다 작기 때문에 right의 위치를 mid로 변경한다.

• right = mid = 7
  

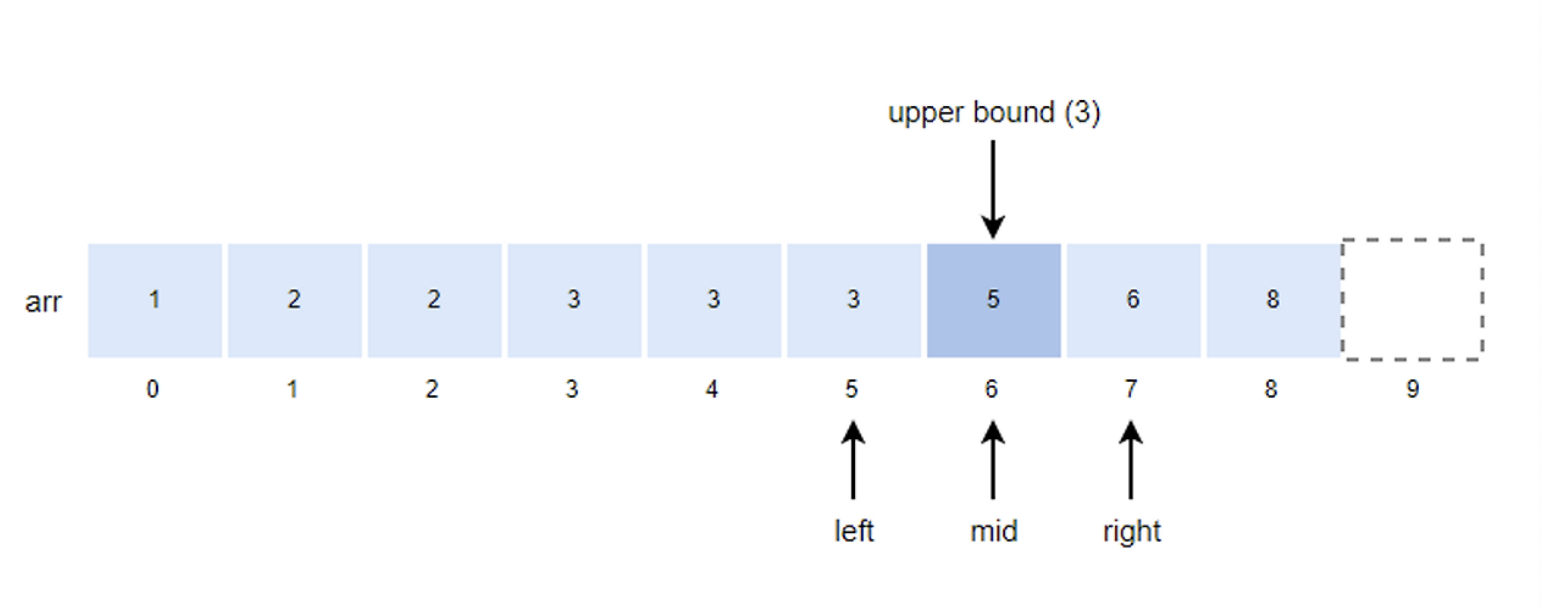
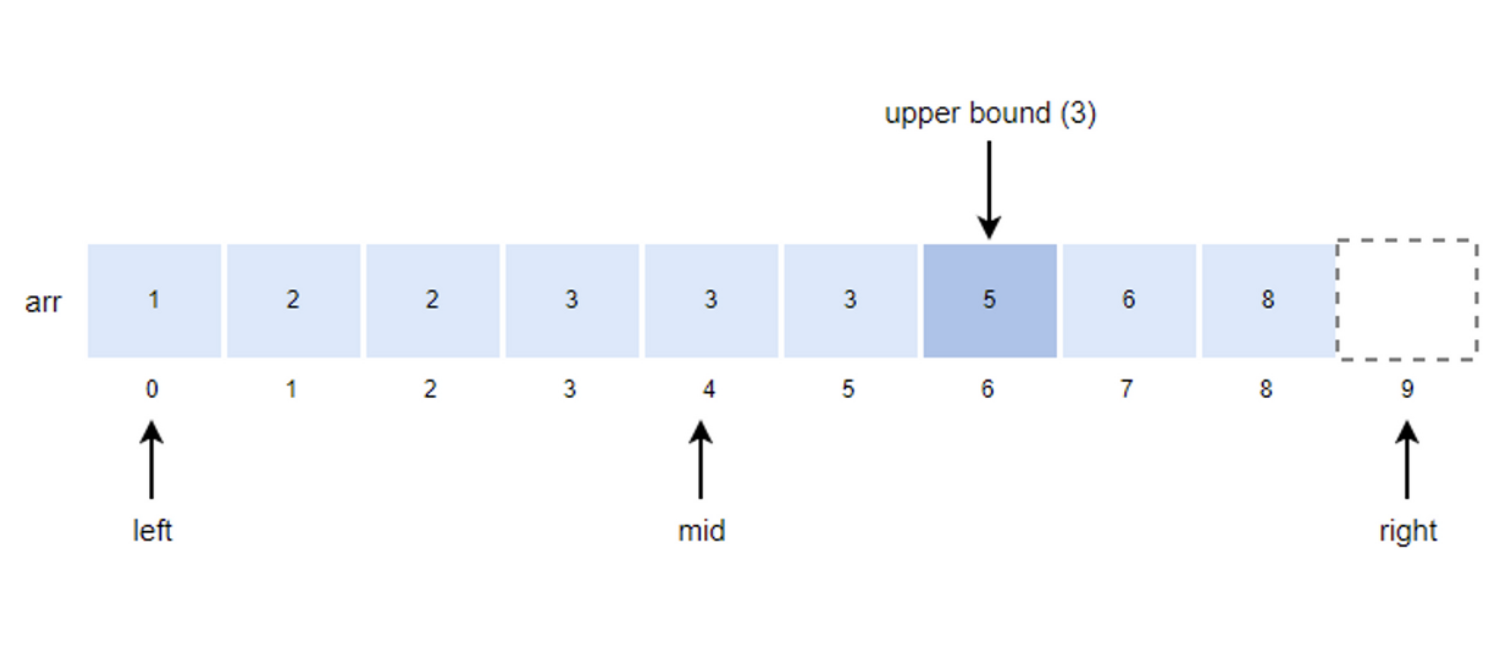
5. mid값을 구하고 k값과 비교한다.

• mid = (left + right)/2 = (5+7)/2 = 6
  

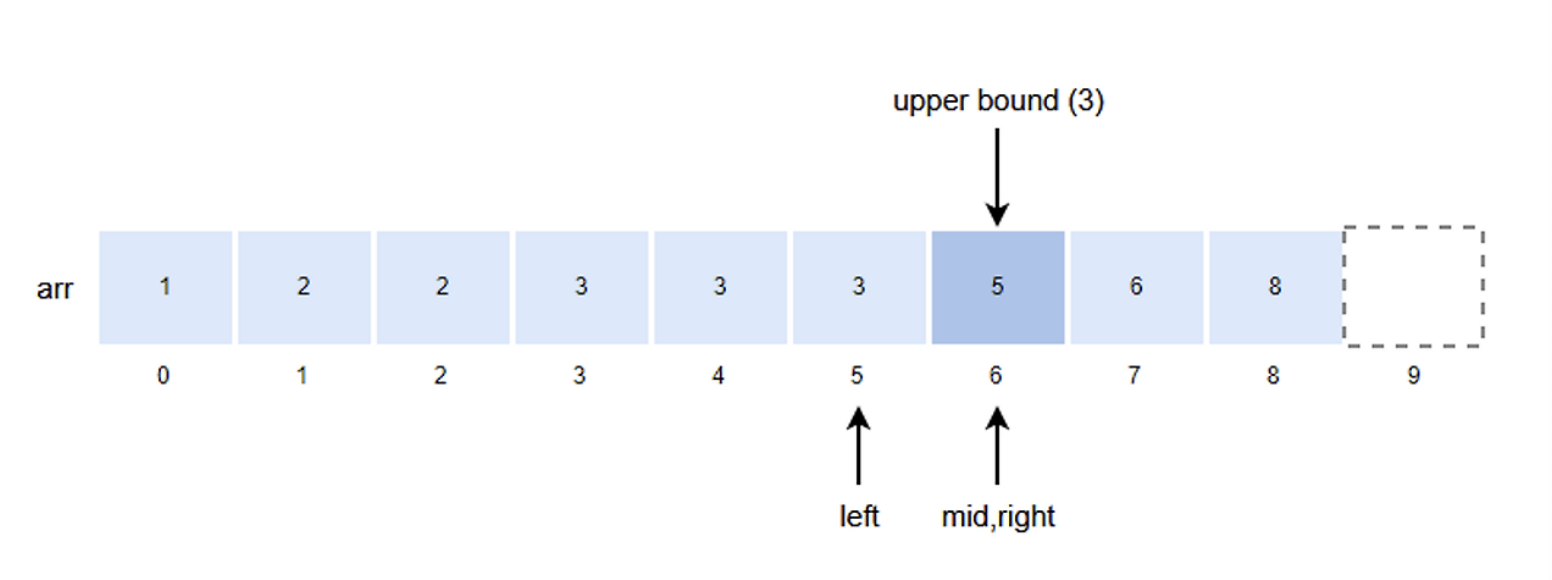
6. k값이 arr[mid]값보다 작기 때문에 right의 위치를 mid로 변경한다.

• right = mid = 6
  

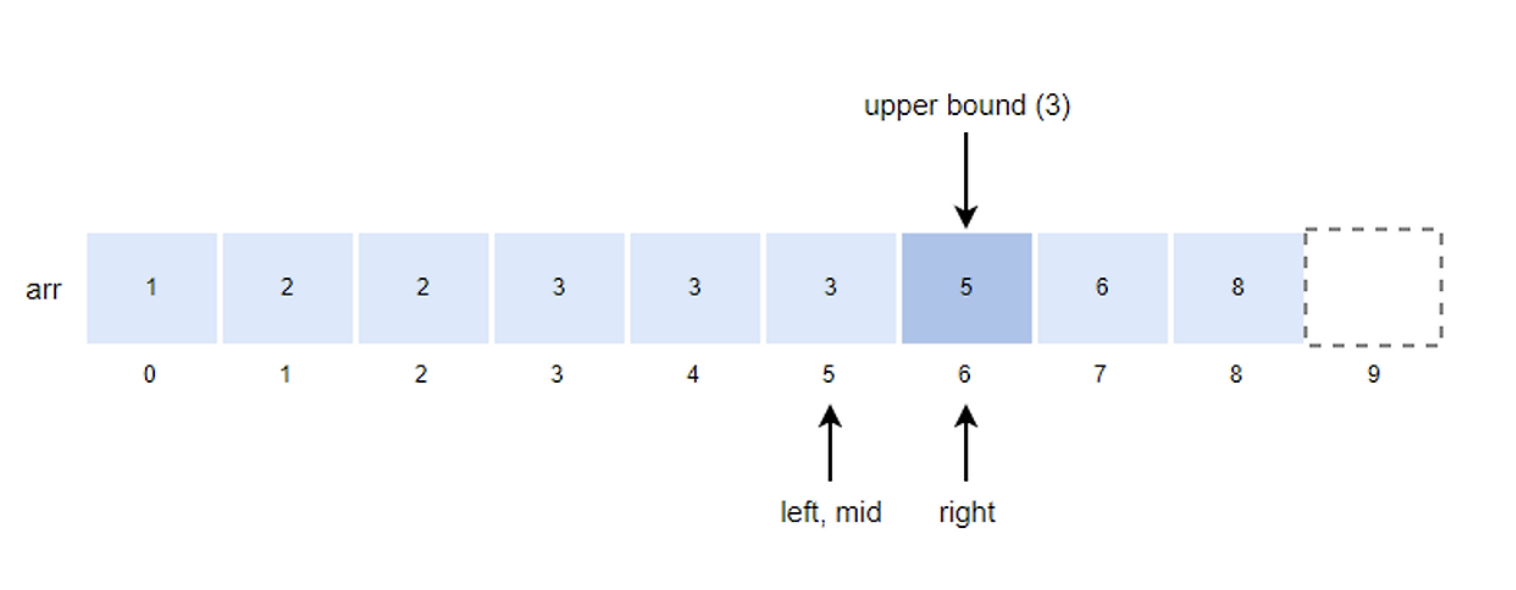
7. mid값을 구하고 k값과 비교한다.

• mid = (left + right)/2 = (5+6)/2 = 5
  

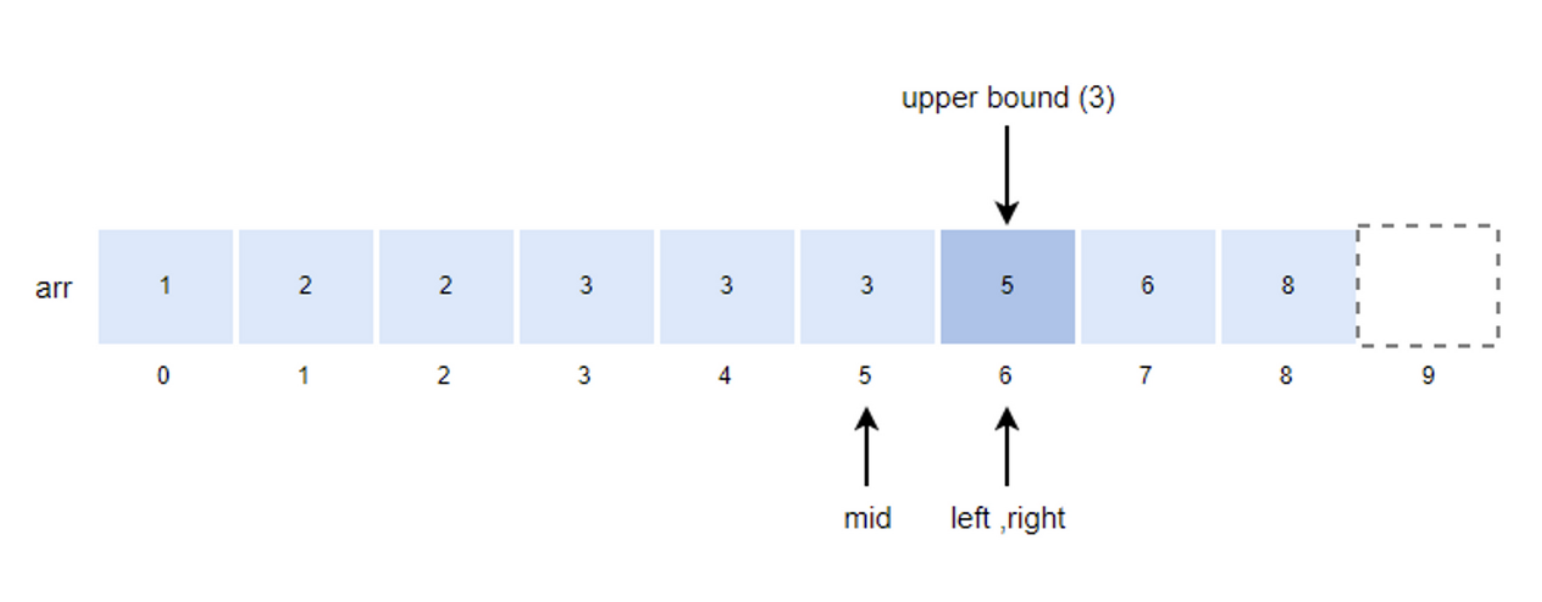
8. k값이 arr[mid]값과 같기 때문에 left의 위치를 mid + 1로 변경한다.

• left = mid + 1 = 5 + 1 = 6
• left값이 right값과 같기 떄문에 루프를 종료하고 right값이 upper bound값이 된다.

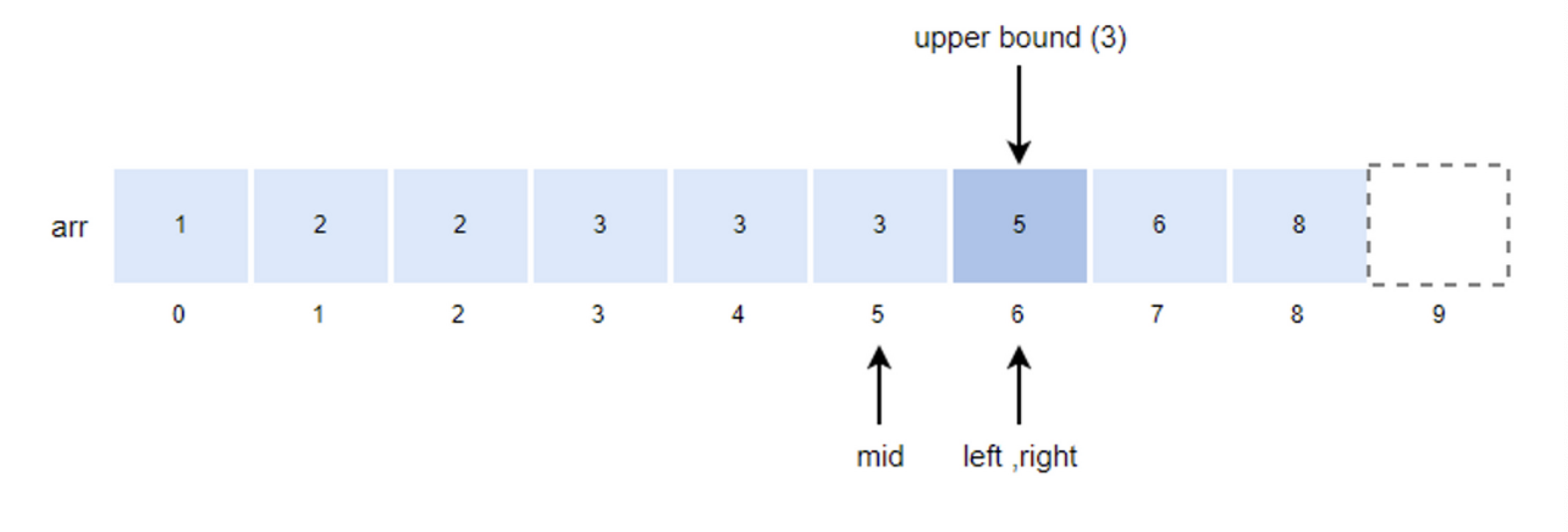
구현

arr배열에서 k값의 upper bound를 찾는 코드

• 매개 변수로 left는 배열의 시작위치, right는 arr의 길이로 받는다.

def upper_bound(arr, left, right, k):
	while left < right:
		mid = (left + right)//2
		if arr[mid] <= k:
			left = mid + 1
		else:
			right = mid
		
	return right

정확히 일치하는 값이 없더라도, 그 값보다 큰 첫번째 원소의 위치를 반환한다.

[ref.블로그]

👍 파이썬에서 bisect모듈을 사용해 정렬된 리스트에서 이진탐색을 수행하는 함수 제공

import bisect

arr = [1, 2, 3, 3, 3, 4, 5]
x = 3

# Lower bound
left_index = bisect.bisect_left(arr, x)
print(f"Lower bound of {x}: {left_index}")  # 출력: 2

# Upper bound
right_index = bisect.bisect_right(arr, x)
print(f"Upper bound of {x}: {right_index}")  # 출력: 5

# 특정 값의 개수 구하기
count = right_index - left_index
print(f"Count of {x}: {count}")  # 출력: 3

bisect.bisect_left는 lower bound 역할을 한다.
위 예시에서 배열 arr에서 x의 lower bound를 찾음

bisect.bisect_right는 upper bound와 동일한 역할을 한다.
위 예시에서 정렬된 리스트 arr에서 x를 삽입할 수 있는 가장 오른쪽 인덱스 반환