문제
두 전봇대 A와 B 사이에 하나 둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생하였다. 합선의 위험이 있어 이들 중 몇 개의 전깃줄을 없애 전깃줄이 교차하지 않도록 만들려고 한다.
예를 들어, < 그림 1 >과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다.
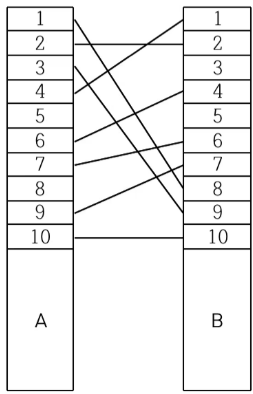
전깃줄이 전봇대에 연결되는 위치는 전봇대 위에서부터 차례대로 번호가 매겨진다. 전깃줄의 개수와 전깃줄들이 두 전봇대에 연결되는 위치의 번호가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는 위치의 번호가 차례로 주어진다. 위치의 번호는 500 이하의 자연수이고, 같은 위치에 두 개 이상의 전깃줄이 연결될 수 없다.
출력
첫째 줄에 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 출력한다.
풀이
모든 전깃줄이 교차하지 않을 때의 가능한 전깃줄의 최대 갯수 = 전깃줄의 위치 배열에서 가장 긴 증가하는 부분 수열의 길이
그림을 보면 A의 인덱스 순서에 대해 B 가 8,2,9,1,4,6,7,10 으로 되어 있다. 이걸 배열 arr 이라고 할때, 배열 arr 의 가장 긴 증가하는 부분 수열이 구하고자 하는 교차하지 않는 전깃줄의 최대 개수가 된다.
주의할점은 A를 기준으로 B를 정렬해야지, B가 자신의 값을 기준으로 1,2,4,6,7,8,9,10 으로 정렬해버리면 교차 여부를 알 수 없게 된다. 따라서 A를 기준으로 정렬해야 B 값이 증가할때 교차하지 않음을 보장할 수 있다.
GPT가 잘 정리해주어서 아래 남긴다.
다듬기 전 코드
n = int(input())
arr = []
for _ in range(n):
l, r = map(int, input().split())
arr.append((l,r))
arr.sort(key=lambda x: x[0])
arr_sub = []
for lv, rv in arr:
arr_sub.append(rv)
dp = [1 for _ in range(len(arr_sub))]
for i in range(1, len(arr_sub)):
for j in range(0, i):
if arr_sub[i] > arr_sub[j]:
dp[i] = max(dp[i], dp[j]+1)
print(n - max(dp)) 다듬은 후 코드
n = int(input())
arr = [tuple(map(int,input().split())) for _ in range(n)]
arr.sort(key=lambda x: x[0])
r_arr = [v for _, v in arr]
dp = [1 for _ in range(n)]
for i in range(1, len(r_arr)):
for j in range(0, i):
if r_arr[i] > r_arr[j]:
dp[i] = max(dp[i], dp[j]+1)
print(n - max(dp))
