[C++] 백준 4948 - 베르트랑 공준

문제 - 베르트랑 공준 (Silver 2)

풀이 전략

• 다른 소수에 관련된 문제를 푸는 방식과 똑같이 하지만, n보다 크고 2n보다 작은 범위 내의 소수의 개수를 구하는 문제이므로 범위를 수정해야 한다.
• 에라토스테네스의 체의 원리를 이해하고 적용한다.

참고

에라토스테네스의 체

=> 특정 범위 내의 소수를 찾는데 효율적인 방법

• Step1 : 1을 제외시킨다.
• Step2 : 2를 제외한 2의 배수를 제거시킨다.
• Step3 : 3을 제외한 3의 배수를 제거시킨다.
• Step4 : 4의 배수는 Step2에서 지워졌으므로 5의 배수로 넘어가서 같은 작업을 반복한다.
• StepN : 위의 작업을 계속 반복하다보면 소수들만 남게 된다.

[나무위키] https://namu.wiki/w/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98%20%EC%B2%B4

구현

<M부터 N까지의 소수들을 출력>

	int M,N;
    cin>>M>>N;

    vector<int> A(N+1,1);

    for(int i=2;i<=sqrt(N);i++){
        if(A[i]==1){
            for(int j=i*i;j<=N;j+=i){
                A[j]=0;
            }
        }
    }
    for(int i=M;i<=N;i++){
    	cout<<A[i]<<" ";
    }

소스 코드

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    
    int num;

    while(1){
        cin>>num;
        if(num==0){
            break;
        }

        int count=0;
        vector<int> A(2*num+1,1);

        for(int i=2;i<=sqrt(2*num);i++){
            if(A[i]==1){
            	for(int j=i*i;j<2*num+1;j+=i){
                	A[j]=0;
            	}
            }
        }
        for(int i=num+1;i<=2*num;i++){
            if(A[i]==1){
                count++;
            }
        }
        cout<<count<<'\n';
    }
    return 0;
}

n부터 2n까지이므로 vector의 size도 2 x num + 1이고, 반복문의 범위도 2 x num + 1까지이다.

결과

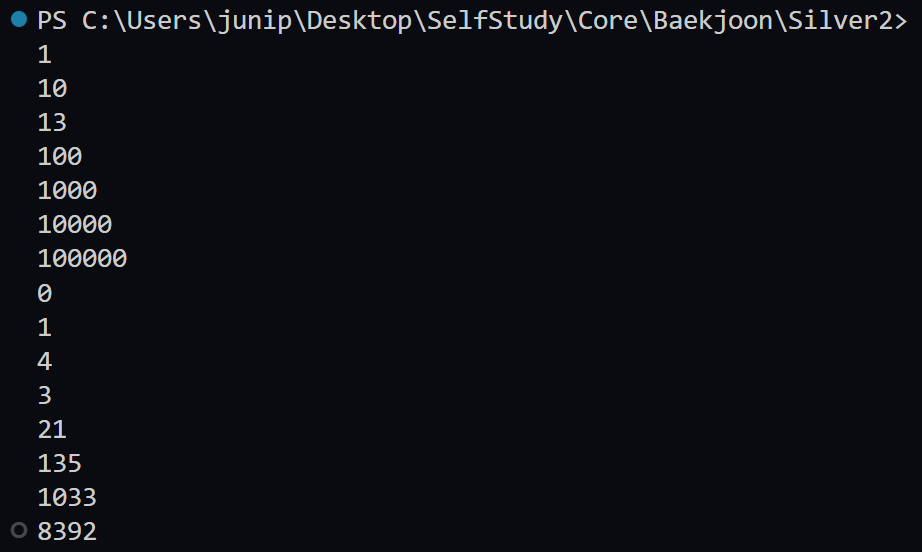
결론

• 특정 구간 내의 소수를 구할 때는 에라토스테네스의 체가 효율적인 것 같다.
• 반복문에서 등호에 조심해야 한다. (처음에 i<=sqrt(num) 이부분에서 등호를 안넣었어서 결과값이 1씩 차이가 났었다)