[C++] 백준 24726 - 미적분학 입문하기 2

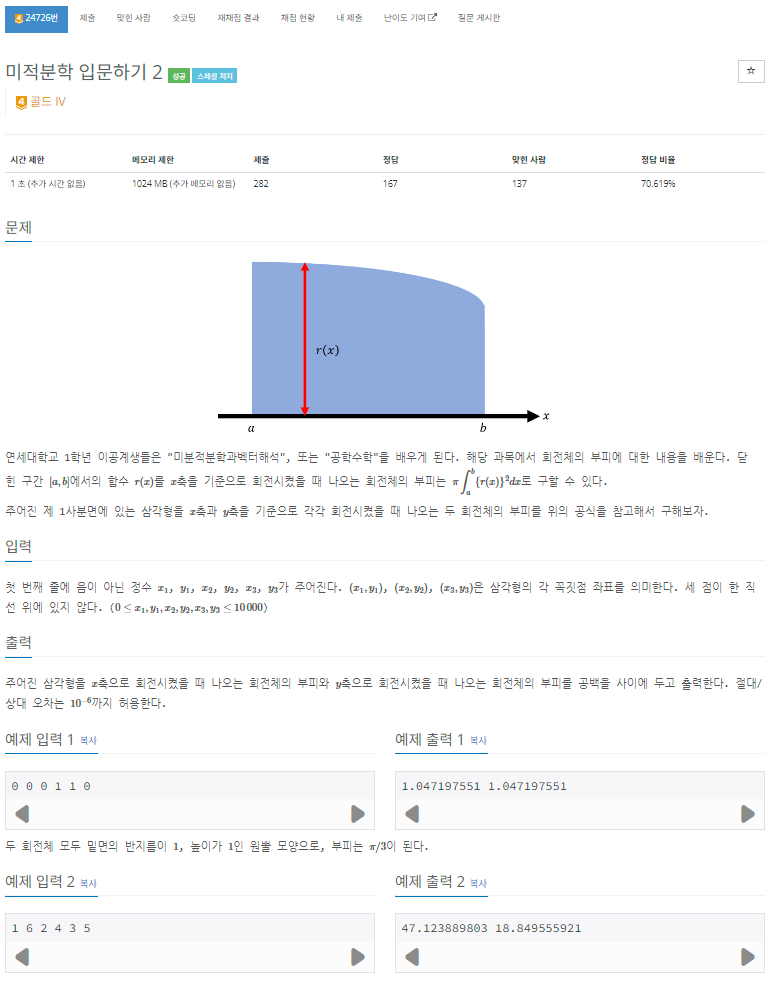
문제 - 미적분학 입문하기 2 (Gold4)

[백준 24726] https://www.acmicpc.net/problem/24726

풀이 전략

• 삼각형을 각각 x축, y축에 대해 회전시킨 회전체의 부피를 구하는 문제이기 때문에 파푸스의 정리를 이용할 것이다.
• 파푸스의 정리를 사용하기 위해, CCW 알고리즘을 이용해 삼각형의 면적을 구하고, 삼각형을 돌리기 위해 무게 중심을 구할 것이다.

참고

[ccw알고리즘]

흔히 알고 있는 것은 신발끈 공식인데 선형대수적 관점으로 바라보면 외적을 구하는 방식이다. 이 문제에서는 삼각형의 면적을 구할거기 때문에 외적을 통해 구해지는 평행사변형의 면적에 1/2배를 해줘야 한다.

[파푸스의 정리]

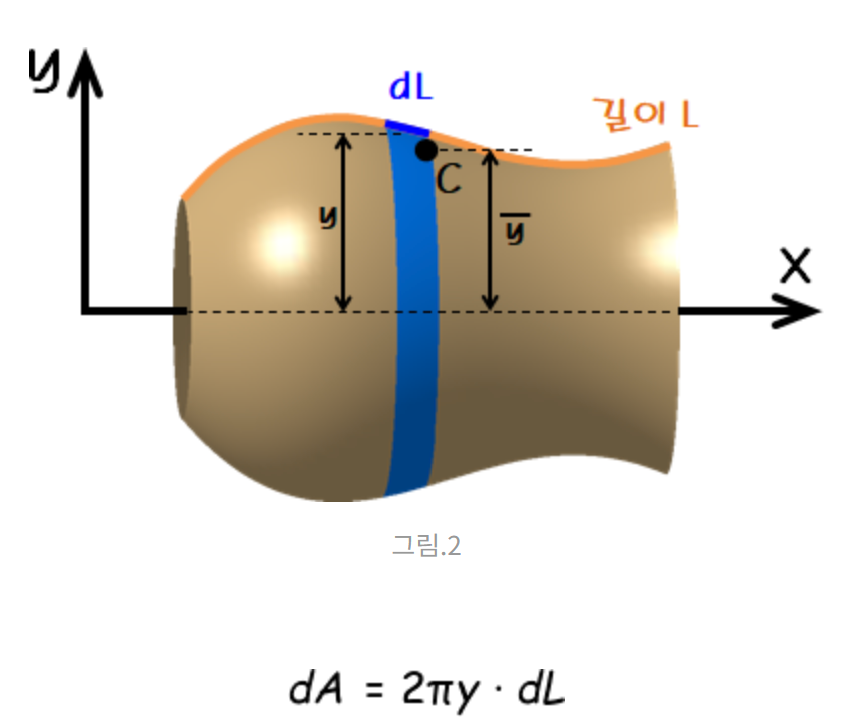
파푸스의 정리는 회전체의 부피, 특히나 토러스를 구할 때 사용되는데, 2차원 평면에서 회전시킬 도형의 면적 x 2 x $pi$ x 도형의 무게중심으로 구할 수 있다.

소스 코드

#include <iostream>
#include <cmath>
using namespace std;

const double PI=3.141592;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int x1,y1,x2,y2,x3,y3;
    cin>>x1>>y1>>x2>>y2>>x3>>y3;

    double CCW=0.0;
    CCW=abs((x1*y2+x2*y3+x3*y1)-(x2*y1+x3*y2+x1*y3))/2;
    // 삼각형의 면적이기 때문에 1/2배
    
    double CG_X=(x1+x2+x3)/3.0; // 무게중심의 X좌표
    double CG_Y=(y1+y2+y3)/3.0; // 무게중심의 Y좌표

    double Rotate_X=2*PI*CG_Y*CCW; // X축 회전
    double Rotate_Y=2*PI*CG_X*CCW; // Y축 회전

    cout<<fixed;
    cout.precision(10); // 소수점 이하 10자리 고정
    cout<<Rotate_X<<" "<<Rotate_Y<<'\n';
    return 0;
}

결과