[C++] 백준 21919 - 소수 최소 공배수

문제 - 소수 최소 공배수 (Silver3)

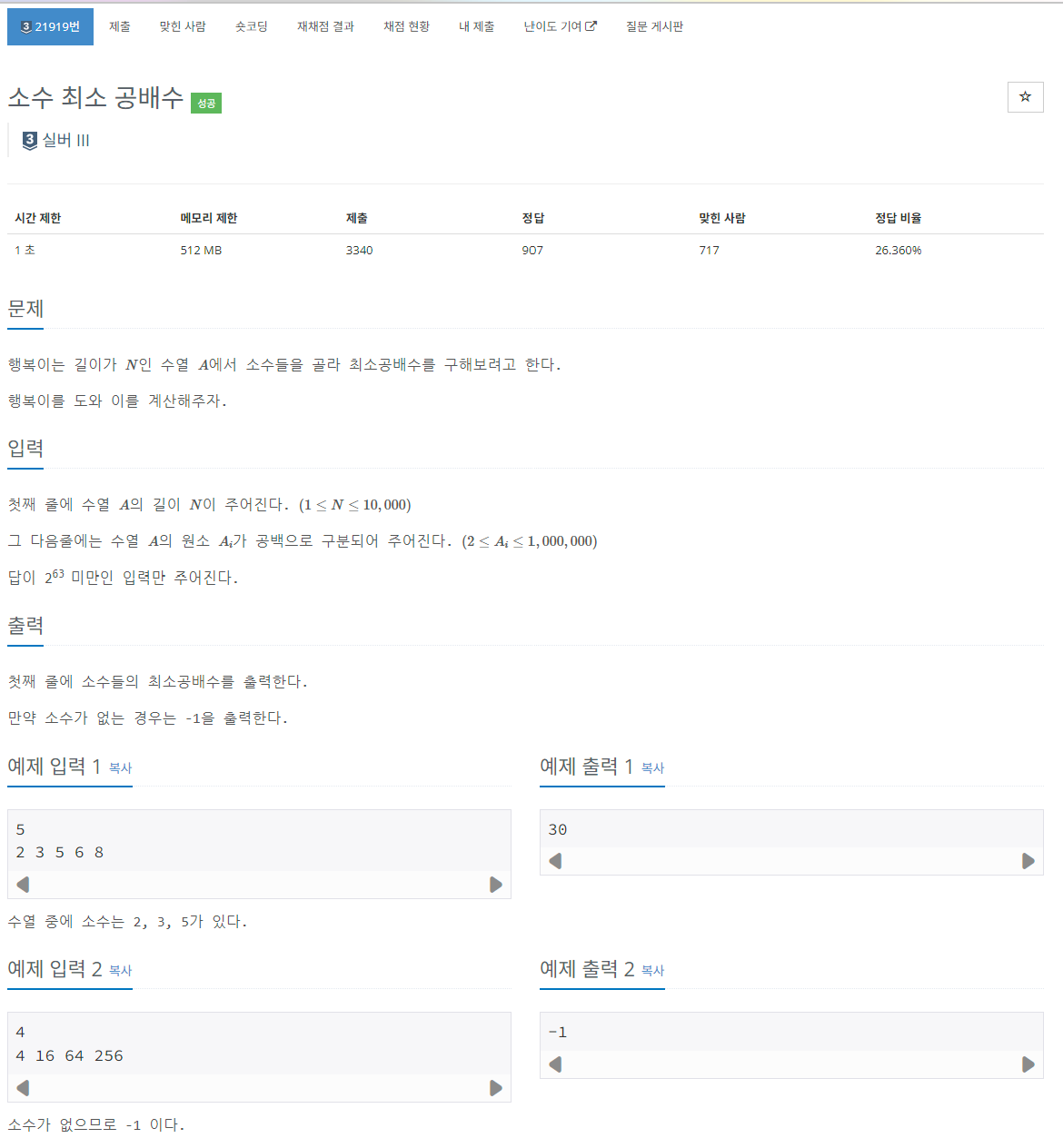
[백준 21919] https://www.acmicpc.net/problem/21919

풀이 전략

• 에라토스테네스와 최대 공약수 알고리즘을 이용해서 문제를 푼다.
• 최소 공배수는 a, b 두 수가 있을 때 a x b / (a와 b의 최대공약수) 임을 이용한다.

소스 코드

잘못된 코드
(답은 맞게 출력되지만, 최대공약수를 구하는 알고리즘을 사용하지 않았다.)
-> 소수들의 최소공배수는 그냥 소수들을 곱해주면 된다고 생각해서 구현

#include <iostream>
#include <cmath>
#include <vector>

#define MAX_NUM 1000
using namespace std;

int N, num;
vector<int> A(MAX_NUM+1,1);
// 에라토스테네스의 체로 거를 전체 숫자들
vector<int> B;
// 소수만 저장해놓은 배열
vector<int> C;
// 입력값이랑 일치하는 소수들만 저장해놓은 배열

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    cin>>N;
    
    for(int i=2;i<=sqrt(MAX_NUM);i++){
        for(int j=i*i;j<=MAX_NUM;j+=i){
            A[j]=0;
        }
    }
    // 에라토스 테네스의 체
    
    for(int i=2;i<MAX_NUM;i++){
        if(A[i]==1)
            B.push_back(i);
    }
    
    for(int i=0;i<N;i++){
        cin>>num;
        for(int j=0;j<MAX_NUM;j++){
            if(num==B[j]){
                C.push_back(num);
            }
        }
    }
    // B에 들어있는 소수랑 입력값이랑 같으면 C에 복사

    int result=1;
    for(int i=0;i<C.size();i++){
        result*=C[i];
    }
    // 소수들은 최소공배수가 곧 

    if(!C.empty()){
        cout<<result<<'\n';
    }else{
        cout<<"-1"<<'\n';
    }
    return 0;
}

정답

#include <iostream>
#include <cmath>
#include <vector>

#define MAX_NUM 1000001
using namespace std;

long long N, num;
vector<long long> A(MAX_NUM+1,1);
vector<long long> B;

void Eratostenes(){
    for(int i=2;i<=sqrt(MAX_NUM);i++){
        for(int j=i*i;j<=MAX_NUM;j+=i){
            A[j]=0;
        }
    }
    for(int i=2;i<MAX_NUM;i++){
        if(A[i]==1){
            B.push_back(i);
        }
    }
} // 에라토스테네스의 체

long long gcd(long long a, long long b){
    if(b==0){
        return a;
    }else{
        return gcd(b,a%b);
    }
} // 최대공약수

long long lcm(long long a, long long b){
    return a*b/gcd(a,b);
} // 최소공배수

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    cin>>N;
    Eratostenes();

    long long answer=1;

    int num;
    for(int i=0;i<N;i++){
        cin>>num;
        for(int j=0;j<B.size();j++){
            if(num==B[j])
                answer=lcm(answer,num);
        }
    }

    if(answer==1){
        cout<<"-1"<<'\n';
    }else{
        cout<<answer<<'\n';
    }
    return 0;
}

결과