[C++] 백준 1932 - 정수 삼각형

문제 - 정수 삼각형 (Silver 1)

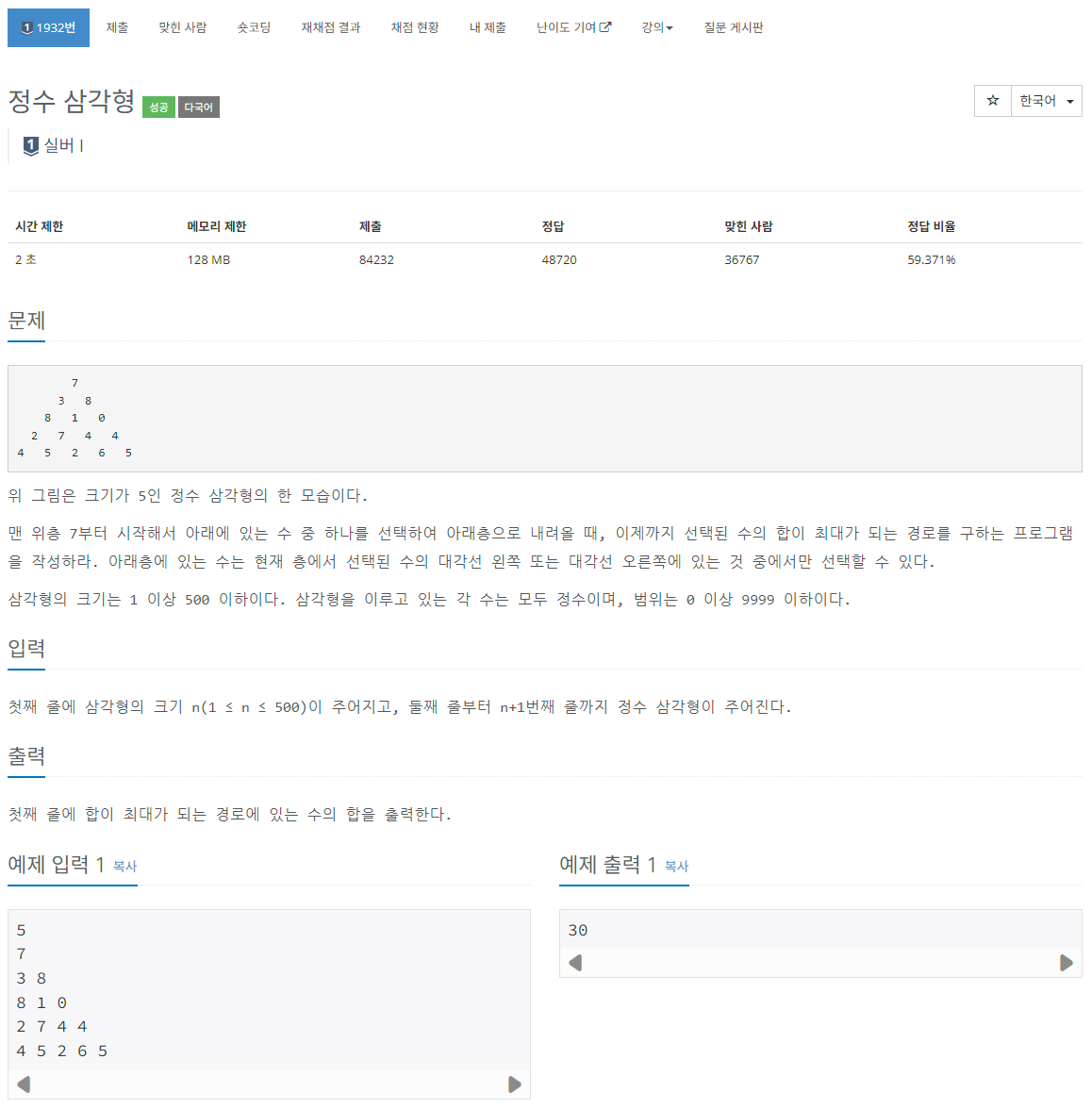
[백준 1932] https://www.acmicpc.net/problem/1932

풀이 전략

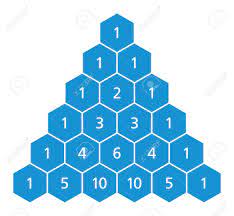
• 문제를 보자 마자 파스칼의 삼각형 이론을 적용하면 점화식을 쉽게 구할 수 있을 것이라고 생각했다.
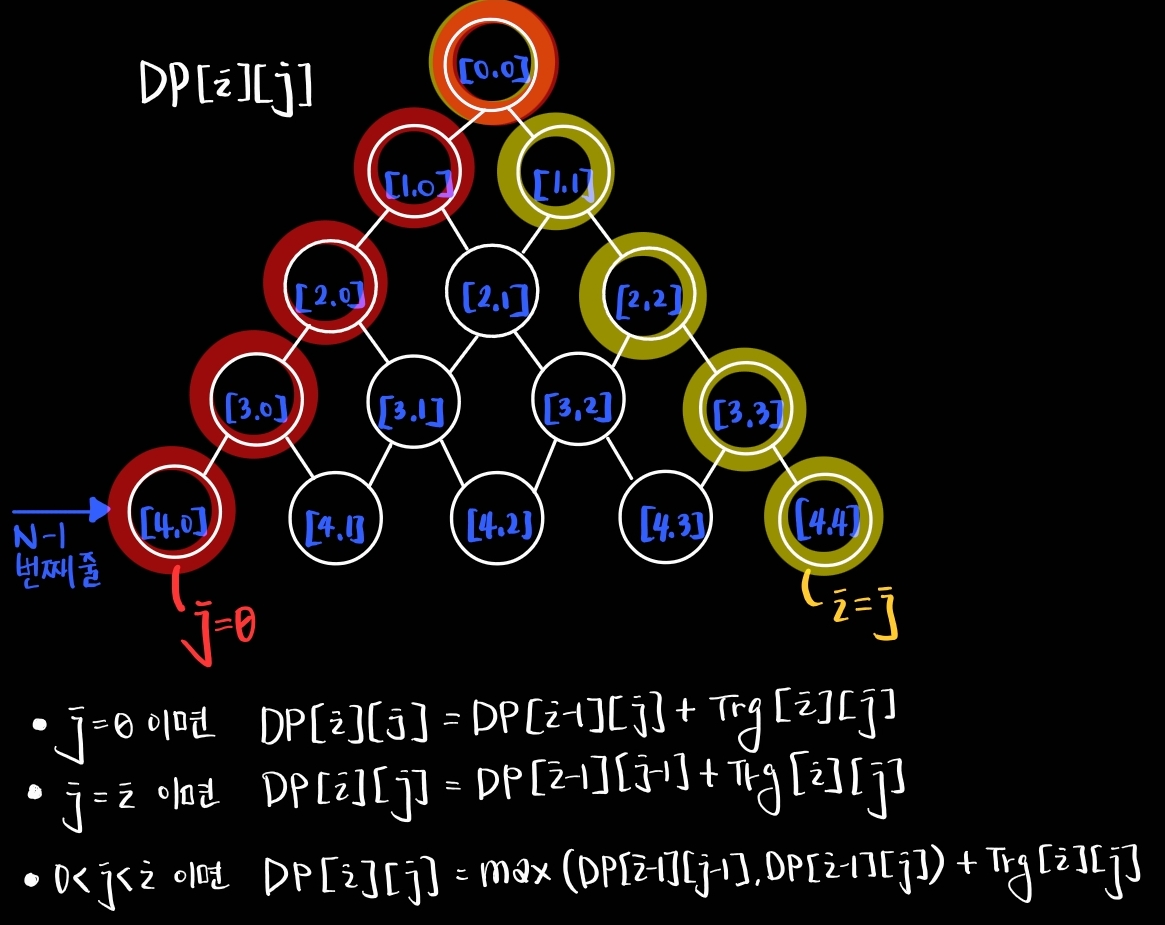
• 2차원 배열로 DP 배열을 만든 뒤 DP[i][j]는 DP[i-1][j-1], DP[i-1][j] 배열 값 중 최댓값에 입력값을 더해서 이차원 배열에 저장해 놓은 뒤, 마지막 줄에서의 최댓값을 출력하면 된다.
  (문제 조건에서, "아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다." 라고 주어져 있기 때문)
• 파스칼 삼각형 공식 : DP[i][j]=DP[i-1][j-1]+DP[i-1][j]

*자세한 설명은 아래 그림에 설명해 두었다.

소스 코드

#include <iostream>
#include <vector>

 #define MAX 10000
 using namespace std;

 int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N;
    cin>>N;
    vector<vector<int>> Trg(N,vector<int>(N,0));

    for(int i=0;i<N;i++){
        for(int j=0;j<=i;j++){
            cin>>Trg[i][j];
        }
    }

    vector<vector<int>> DP(N,vector<int>(N,0));
    DP[0][0]=Trg[0][0];
    for(int i=1;i<N;i++){
        for(int j=0;j<=i;j++){
            if(j==0){
                DP[i][j]+=(DP[i-1][j]+Trg[i][j]);
                // j==0이면 오른쪽 위가 최대
            }else if(j==i){
                DP[i][j]+=(DP[i-1][j-1]+Trg[i][j]);
            	// j==i일 때도 왼쪽 위가 최대
            }else{
                DP[i][j]+=(Trg[i][j]+max(DP[i-1][j-1],DP[i-1][j]));
                // 0<j<i 인 경우는 왼쪽 위와 오른쪽 위를 비교해야 함
            }
        }
    }
    int result=0;
    for(int i=0;i<N;i++){
        result=max(result,DP[N-1][i]);
    }
    / DP 배열을 저장한 뒤, 제일 마지막 줄에서 최댓값을 출력
    cout<<result<<'\n';
    return 0;
 }

결과

참고

• DP 배열을 저장했을 때 DP 배열에 저장된 값들 확인

    for(int i=0;i<N;i++){
        for(int j=0;j<=i;j++){
            cout<<DP[i][j]<<" ";
        }
        cout<<'\n';
    }

위의 코드를 추가하면, DP 배열에 저장된 값들을 확인할 수 있다.