[C++] 백준 16931 - 겉넓이 구하기

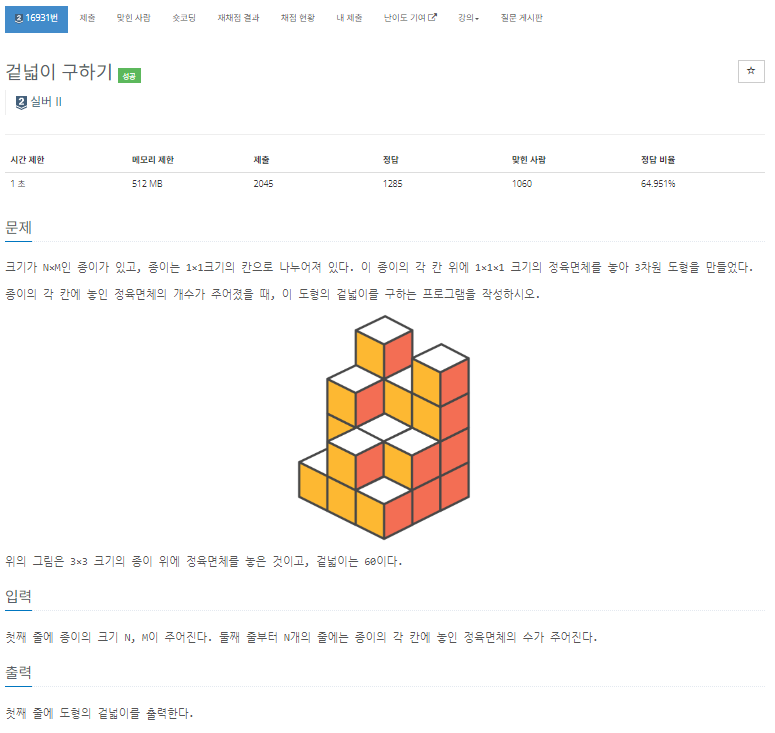
문제 - 겉넓이 구하기 (Silver 2)

[백준 16931] https://www.acmicpc.net/problem/16931

풀이 전략

• 처음에는 예제를 통해 접근을 했는데

3 3
1 3 4
2 2 3
1 2 4

각 면을 면과 평행한 위치에서 바라보면 최댓값이 이루는 모양으로 보인다.

따라서 각 행과 열에서의 최댓값들을 더한 뒤, 최댓값이 동일하면 그림에서 4 3 4 사이에 있는 2를 더해주는 전략을 생각했다.
즉 위의 예시에서 1행의 최댓값 4, 2행의 최댓값 3, 3행의 최댓값 4, 1열의 최댓값 2, 2열의 최댓값 3, 3열의 최댓값 4를 모두 더한 20에 밑면의 넓이 9을 더한 29 x 2 = 58에 2를 더한 60이 정답이다! ... 라고 풀려고 보니 그림에서 처럼 최댓값 조합이 4 3 4가 아니라 4 4 3이여도 최댓값은 중복되는데, 가운데 빈공간이 생기지 않아서 2를 더할 필요가 없어지는 반례가 존재한다.
따라서 이 전략을 버리고, 모든 칸들을 탐색하면서 인접하는 칸들과의 차이를 더해도 똑같은 원리로 답이 구해진다는 것을 이용해 문제를 접근했다.

소스 코드

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int dx[]={-1,1,0,0};
int dy[]={0,0,-1,1};

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N,M;
    cin>>N>>M;

    vector<vector<int>> A(N+2,vector<int>(M+2,0)); // 모서리쪽 변을 비교하려면 옆에 한 칸씩 더 필요함

    int TotalA=2*N*M; // 밑면과 윗면의 넓이의 합으로 초기화

    for(int i=1;i<=N;i++){
        for(int j=1;j<=M;j++){
            cin>>A[i][j];
        }
    }
    for(int x=1;x<=N;x++){
        for(int y=1;y<=M;y++){
            for(int k=0;k<4;k++){
                int nx=x+dx[k];
                int ny=y+dy[k];

                if(A[x][y]>A[nx][ny])
                    TotalA+=(A[x][y]-A[nx][ny]);
                // 겹치는 경우 그 차이만큼 더해줌
            }
        }
    }

    cout<<TotalA<<'\n';
    return 0;
}

결과

결론

문제 푸는 방법을 알아도, 반례가 틈만 나면 생겨서 여러 접근 방식에 대해 알아야 할 것 같다. 특히 이런 기하학 문제는 더더욱..