[C++] 백준 1904 - 01타일

문제 - 01타일 (Silver3)

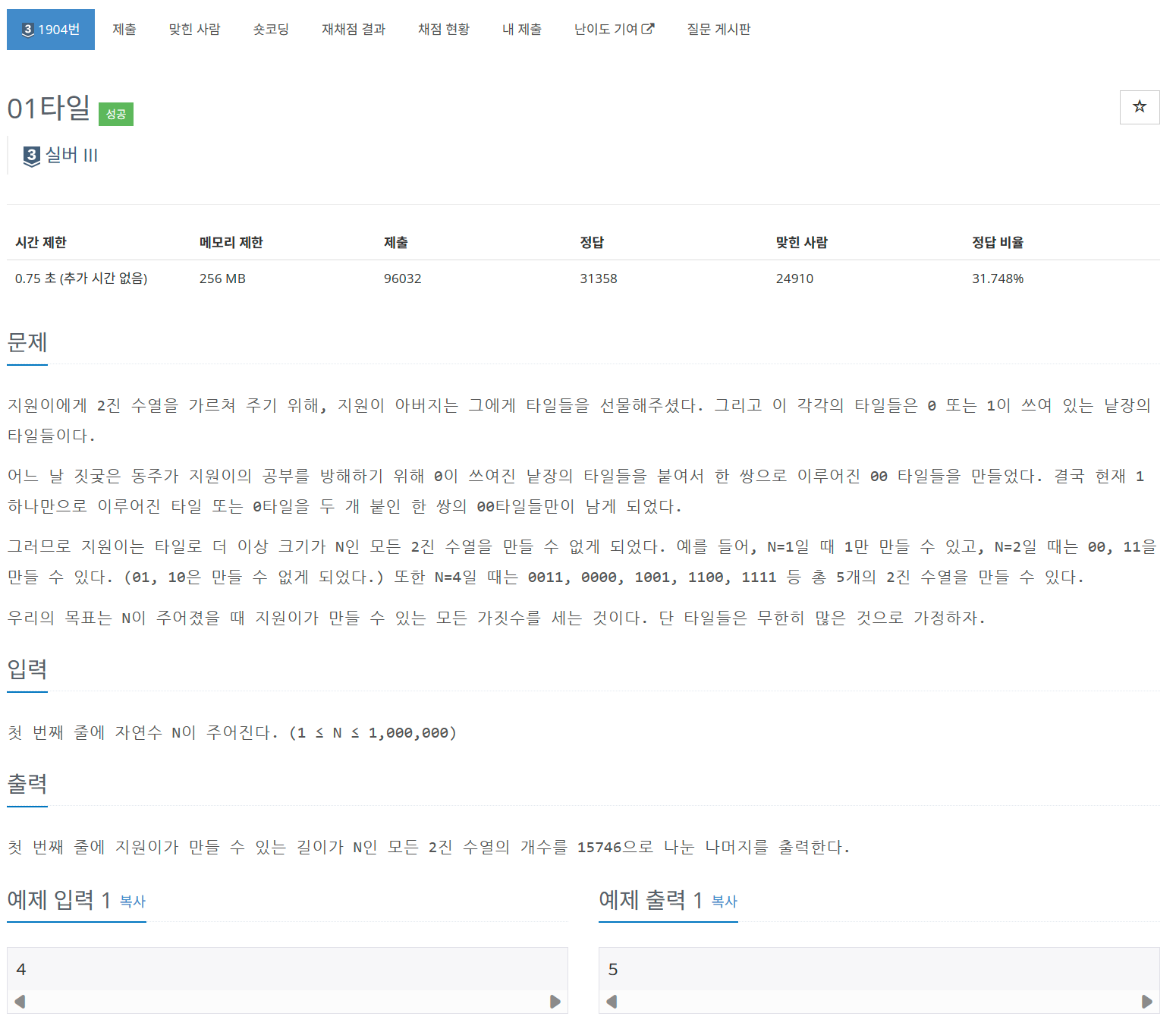
[백준 1904] https://www.acmicpc.net/problem/1904

풀이 전략

N에 따라서 DP 값을 구해서 규칙성을 파악한다.

풀이

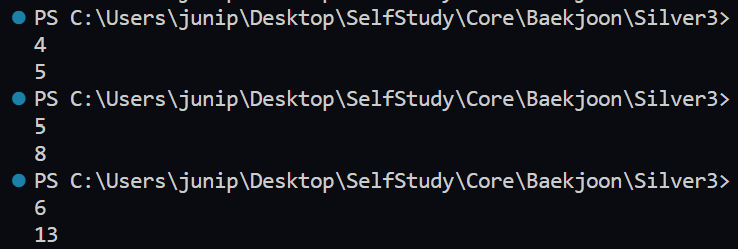
이런 식으로 N에 대해 모든 경우의 수를 나열해보았다. 그런데 이건 00, 1로만 구성하는거라 복잡할 줄 알았는데 N=6까지를 구해보니 피보나치수열이였다.

왜 그럴까?

그 이유는 00과 1의 길이에 있다.
00은 길이가 2이기 때문에 i-1번째 위치에 이어서 붙일 수 없다.

좀 더 이해하기 쉽게 설명하면
N=2일 때의 case는 11과 00 두 가지이고 N=3일 때는 111, 100, 001 세 가지이다.

N(=i)이 홀수 일때는 이전 시행(i-1)에서 1만 더 붙일 수 있고, i-2번째 시행에서는 1과 00 둘 다 붙일 수 있지만, 예를 들어 11->1111의 경우 111->1111과 중복되기 때문에 i-1번째의 경우를 더해주면 되는 것이다.

따라서 $\text{DP}[i]=\text{DP}[i-1]+\text{DP}[i-2]$ 라는 점화식이 도출된다.

소스 코드

#include <iostream>
#include <vector>

#define MAX 10000001
const int MOD=15746;
using namespace std;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    
    int N;
    cin>>N; 

    vector<int> DP(MAX);
    DP[1]=1;
    DP[2]=2;
    for(int i=3;i<=N;i++){
        DP[i]=(DP[i-1]+DP[i-2])%MOD;
    }
    cout<<DP[N]<<'\n';
    return 0;
}

결과