[C++] 백준 17103 - 골드바흐 파티션

메르센고수·2024년 1월 7일

cpp

풀이 전략

풀이

소스 코드

결과

참고

Baekjoon

목록 보기

42/48

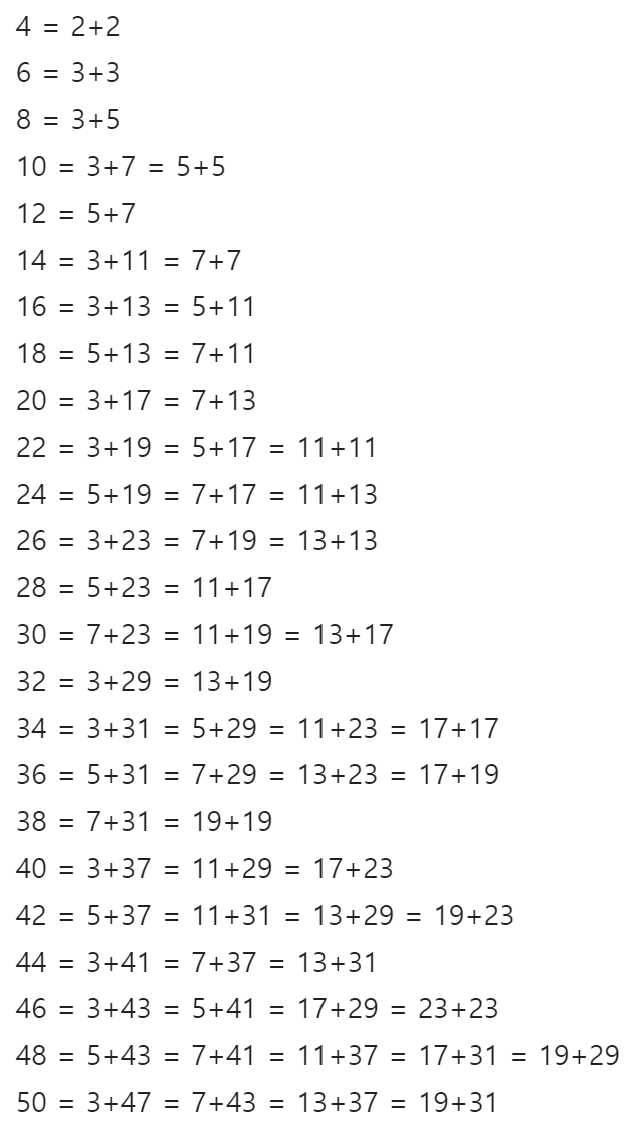
문제 - 골드바흐 파티션 (Silver2)

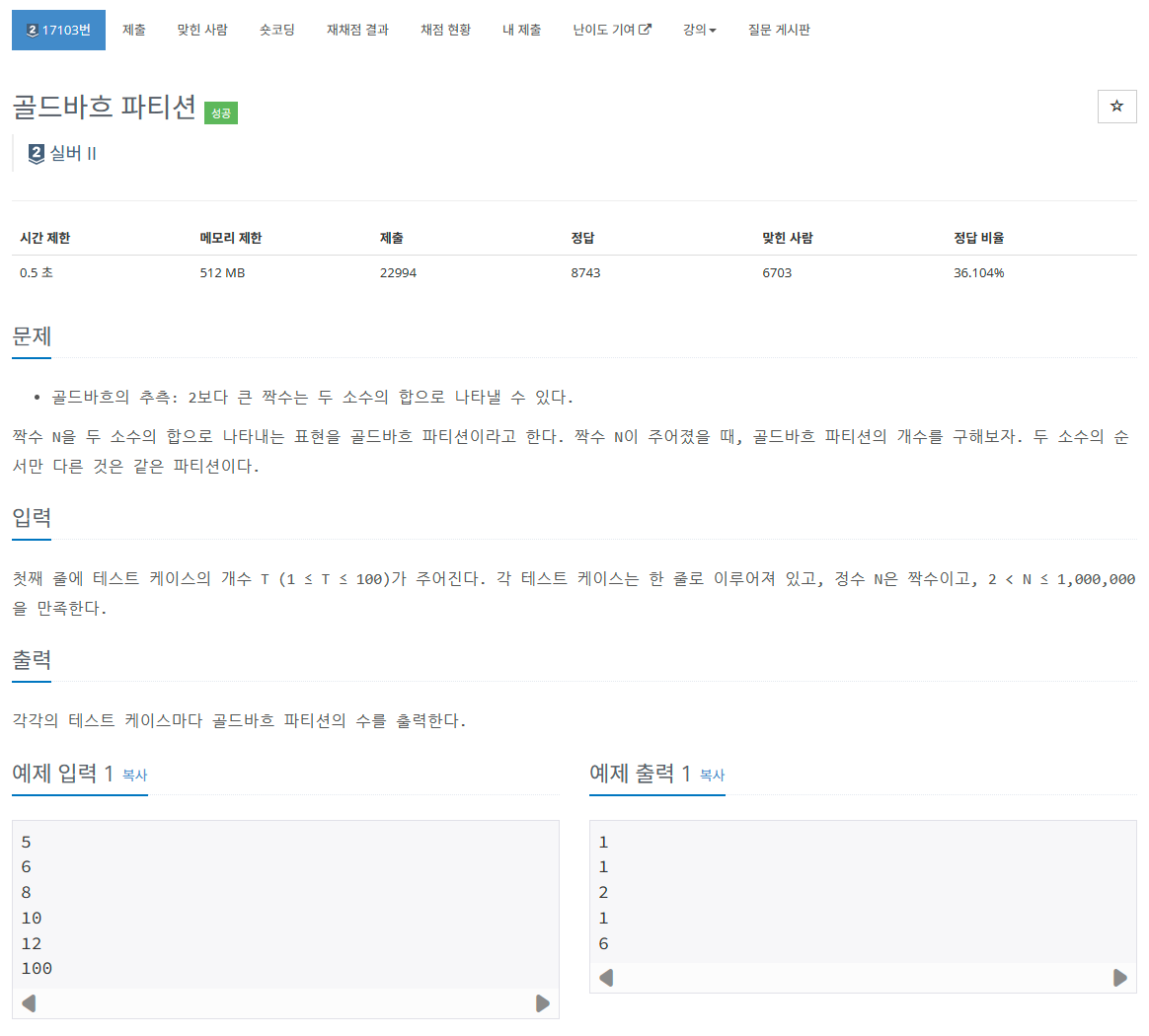
[백준 17103] https://www.acmicpc.net/problem/17103

풀이 전략

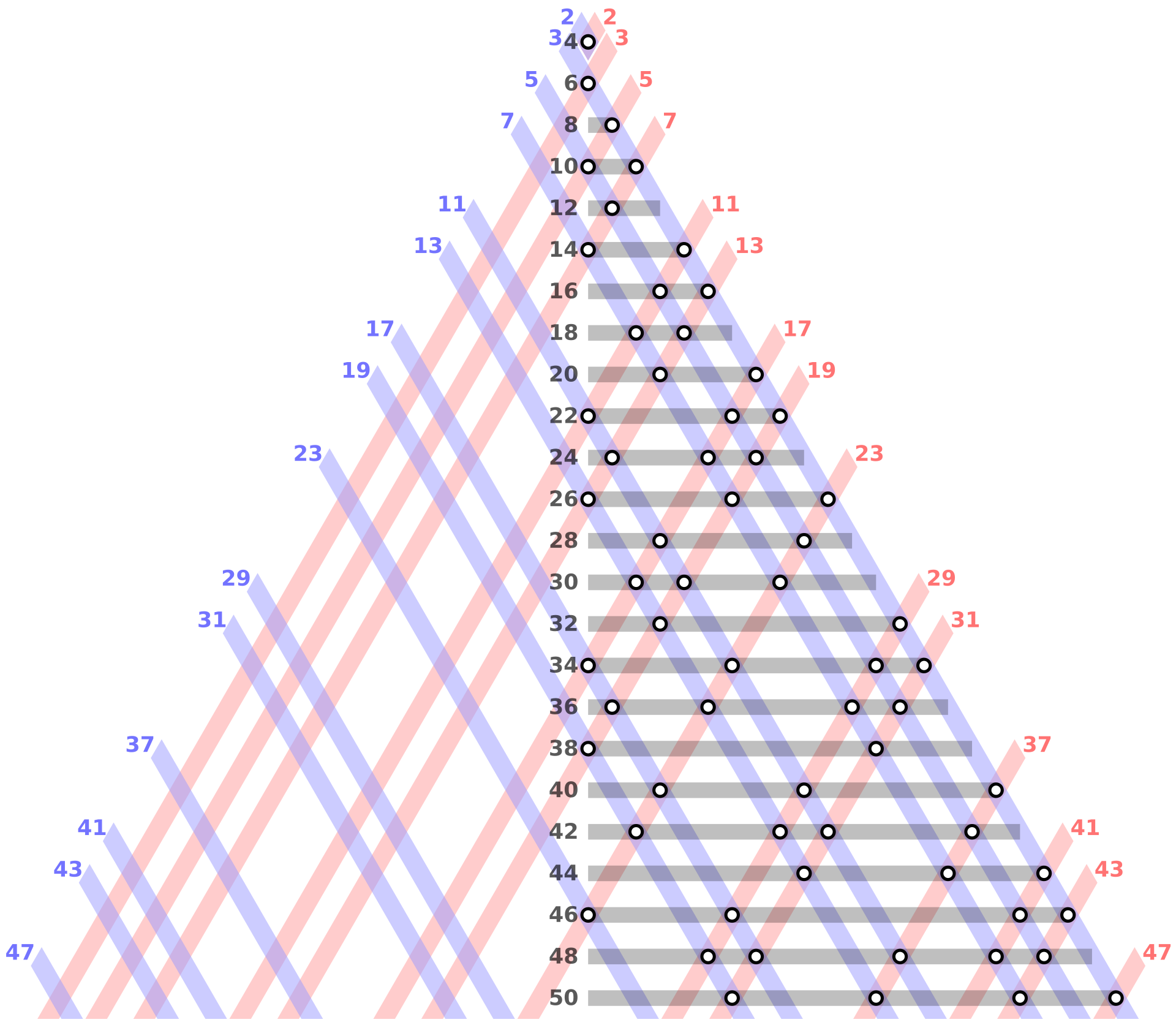
먼저 에라토스테네스의 체 알고리즘으로 소수와 아닌 수를 걸러준 뒤, B 배열에 소수인 수들만 집어 넣어서 B의 배열을 돌면서 입력 받은 N값과 같아지는 합의 경우의 수를 구할 것이다.

골드바흐의 추측

출처 : 위키백과 - 골드바흐의 추측

골드바흐의 추측
: 2보다 큰 모든 짝수는 두 개의 소수(Prime number)의 합으로 표시할 수 있다.
이 때 하나의 소수를 두 번 사용하는 것은 허용한다

풀이

소스코드 아래쪽에 설명해 두었지만, 처음에는 두개의 포인터가 B배열을 돌면서 N과 같아지는 경우의 수를 찾는 과정이 앞에서 부터 시작을 해서 이중 반복문으로 하였지만, 시간복잡도가 N^2이 나오기 때문에 다른 방법으로 접근하였다.
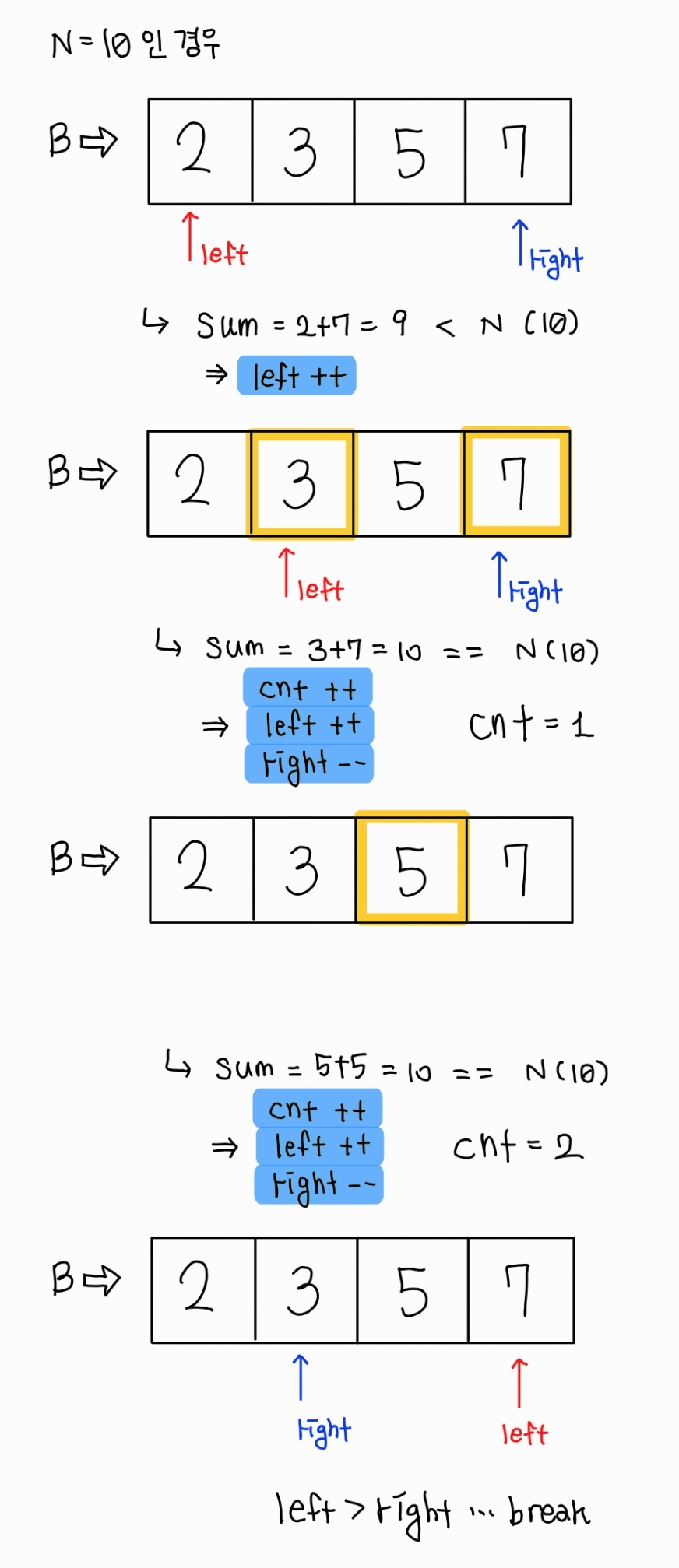
첫번째 시도와 동일하게 두 개의 포인터를 사용하였지만, 하나는 앞에서 다른 하나는 뒤에서 시작해서 N과 같을 때, N보다 클 때, N보다 작을 때 세 가지 경우로 나누어 포인터를 이동시키면서 경우의 수를 구하였다.

소스 코드

#include <iostream>
#include <vector>
#include <cmath>
#define MAX 1000000
using namespace std;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int T;
    cin>>T;
    vector<int> A(MAX+1,1); // 에라토스테네스의 체로 거른 소수 배열
    vector<int> B; // 소수만 넣어놓을 배열
    A[0]=A[1]=0;
    
    // 에라토스테네스의 체
    for(int i=2;i<=sqrt(MAX);i++){
        if(A[i]==0)
            continue;
        for(int j=i*i;j<=MAX;j+=i){
            A[j]=0;
        }
    }

    while(T--){
        int cnt=0; // 각각의 cnt를 구해야 하기 때문에 while문을 돌 때마다 0으로 초기화
        int N;
        cin>>N;
    
    	// N까지의 소수만 B에 저장
        for(int i=2;i<=N;i++){
            if(A[i]==1)
                B.push_back(i);
        }
 
		// 두 개의 포인터 지정 (맨 앞 / 맨 뒤)
        int left=0;
        int right=B.size()-1;

		// 포인터를 이동시키며 sum을 만족시키는 경우의 수 찾기
        while(left<=right){
            int sum=B[left]+B[right];
            if(sum==N){
                cnt++;
                left++;
                right--;
            }else if(sum<N){
                left++;
            }else{
                right--;
            }
        }
        cout<<cnt<<'\n';
        B.clear(); // B 배열을 초기화함
    }
    return 0;
}

아래의 코드는 정답은 맞게 출력되는데 시간 초과 때문에 틀리다고 뜬다.

	...
    while(T--){
        int cnt=0;
        int N;
        cin>>N;
    
        for(int i=2;i<=N;i++){
            if(A[i]==1)
                B.push_back(i);
        }

        int K=B.size();
        for(int i=0;i<K;i++){
            for(int j=i;j<K;j++){
                if(B[i]+B[j]==N)
                    cnt++;
            }
        }
        cout<<cnt<<'\n';
        B.clear();
    }
    ...

코드를 보면, 정답인 코드와의 차이점은 포인터 2개 모두 처음부터 시작해서 한 칸씩 옮겨간다는 점이다. 이를 그림으로 나타내면 다음과 같다.

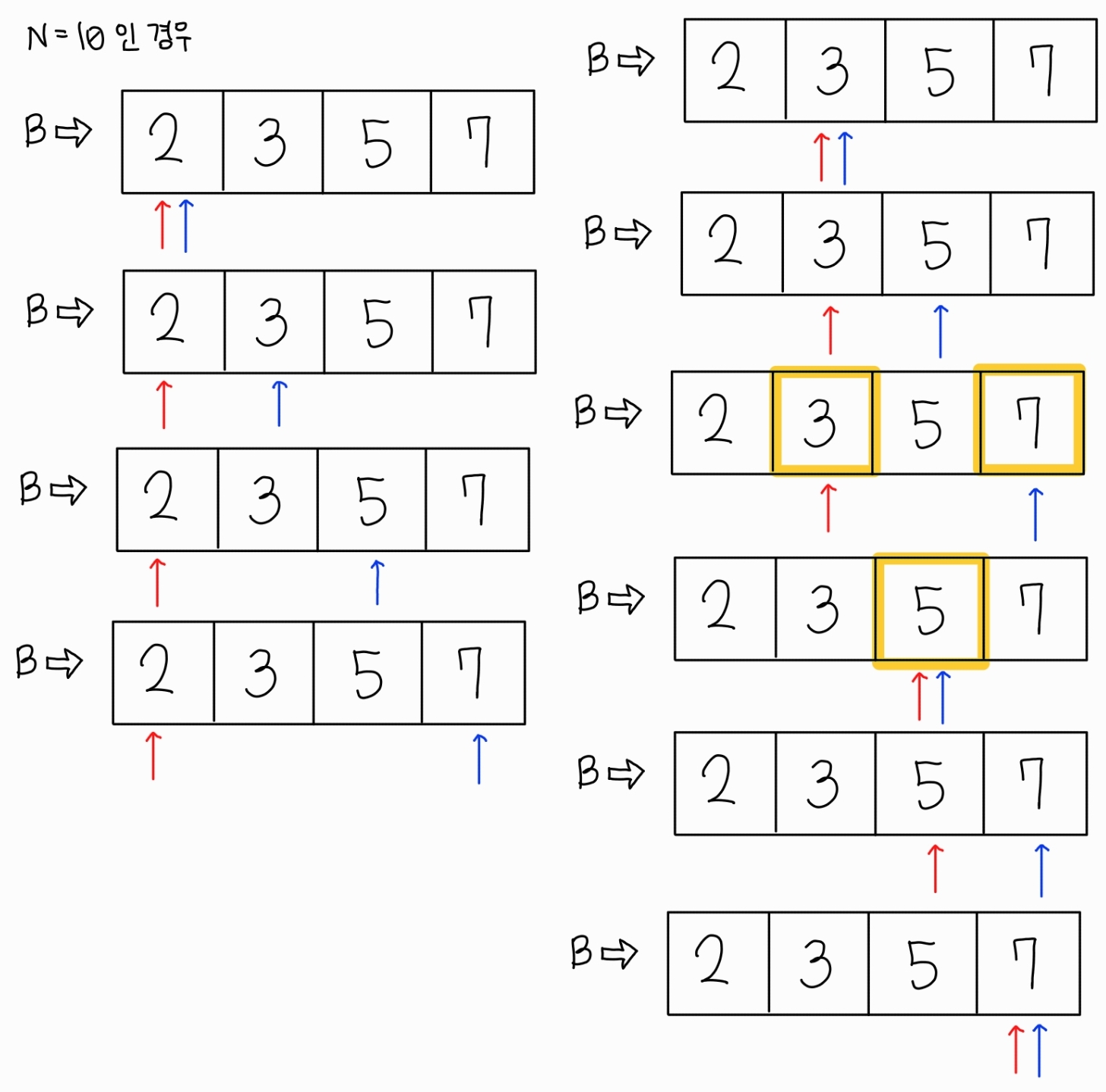
그러나 이 코드의 문제점은, 이미 while문을 돌고 있는데 그 안에서 이중 for문을 돌고 있기 때문에 이미 O(N^2)의 시간복잡도가 발생해서 0.5초의 시간제한을 초과할 수 밖에 없다.
그렇기 때문에 이 방법도 맞는 방법이지만, 첫번째 방법으로 하는 것이 시간복잡도 측면에서 훨씬 효율적이라고 말할 수 있다.