[C++] 백준 16400 - 소수 화폐

문제 - 소수 화폐 (Gold5)

[백준 16400] https://www.acmicpc.net/problem/16400

풀이 전략 / 풀이

이 문제와 풀이가 매우 유사하다.

백준 2293 - 동전 1

그렇기 때문에 2293 문제처럼 DP 점화식을 구하면 되는데, 단순히 2293 문제에서 동전이 소수인 수들로 바뀐점만 차이가 있기 때문에 [에라토스테네스의 체])를 활용하여 소수만 걸러낸 뒤 구하면 된다.그렇기 때문에 2293 문제처럼 DP 점화식을 구하면 되는데, 단순히 2293 문제에서 동전이 소수인 수들로 바뀐점만 차이가 있기 때문에 에라토스테네스의 체를 활용하여 소수만 걸러낸 뒤 구하면 된다.

단, 변수가 있다면 DP[0]=1인 반면, 1은 소수가 아니기 때문에 DP[1]=0이다.
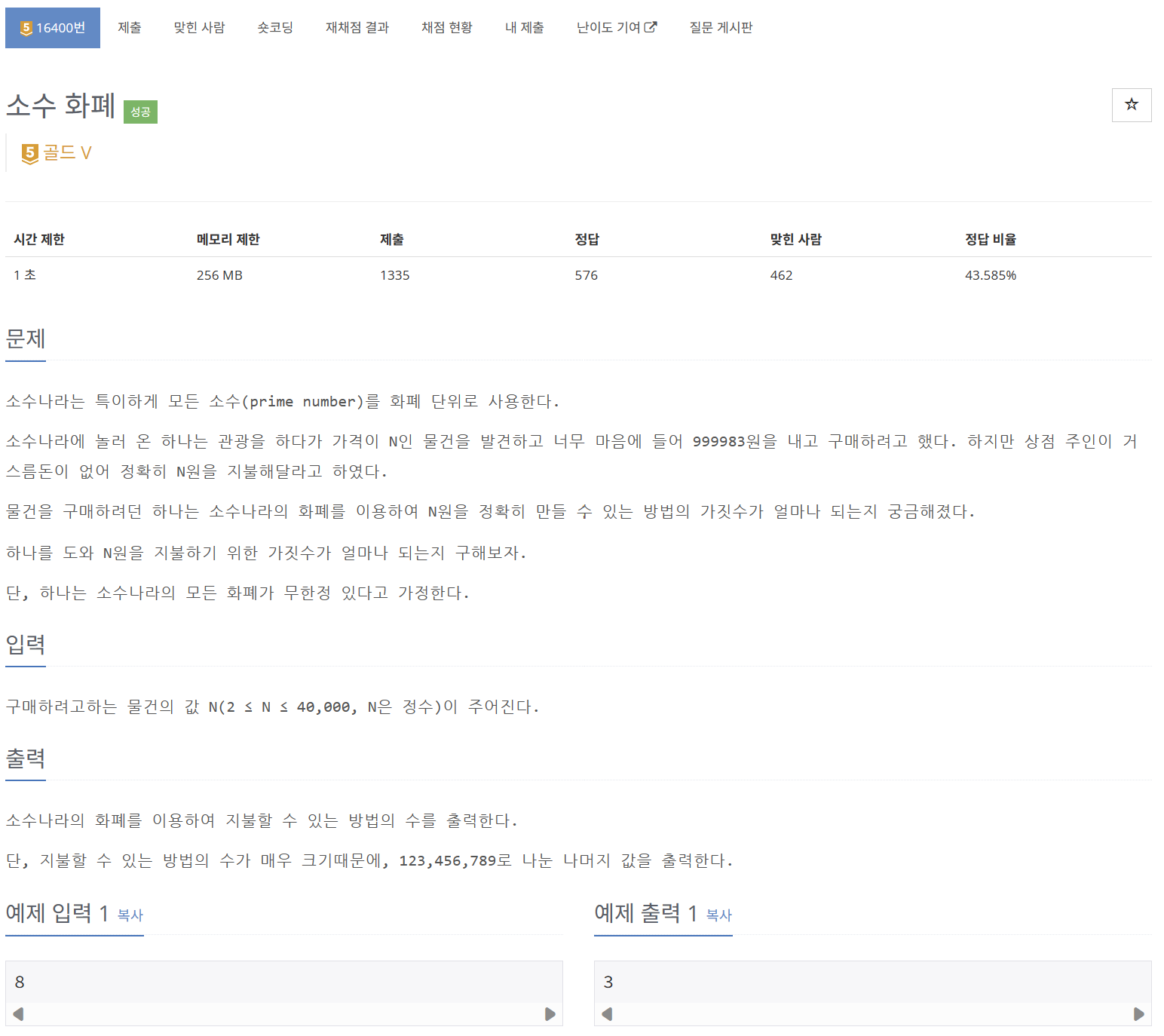
노가다로 DP 값을 구해보면 다음과 같다.

표를 보면, i가 소수 값일 때 자기 자신을 포함해야하기 때문에 1씩 추가되고 2293 문제와 유사한 패턴을 보이는 것을 알 수 있다.

소스 코드

/*문제 : https://www.acmicpc.net/problem/16400
  알고리즘 : 수학, DP, 정수론, 소수판정, 에라토스테네스의 체
  티어 : Gold5
*/
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#define MAX 40001
#define MOD 123456789
using namespace std;

int N;
vector<int> A(MAX+1,1); // 소수를 걸러낼 배열
vector<int> B; // 소수만 집어넣을 배열
long long DP[MAX]={0,}; // DP 배열

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    cin>>N;

	// 에라토스테네스의 체
    A[0]=A[1]=0;
    for(int i=2;i<=sqrt(MAX);i++){
        if(A[i]==1){
            for(int j=i*i;j<=MAX;j+=i){
                A[j]=0;
            }
        }
    }
    for(int i=2;i<=MAX;i++){
        if(A[i]==1){
            B.push_back(i);
        }
    }
    
    // DP 점화식 구하기
    DP[0]=1;
    for(int i=0;i<B.size();i++){
        for(int j=B[i];j<=N;j++){
            DP[j]+=(DP[j-B[i]])%MOD;
            DP[j]%=MOD;
        }
    }
    cout<<DP[N]<<'\n';
    return 0;
}  

결과

결론

동전의 합의 경우의 수를 구하는 문제는 다음과 같이 일반화를 할 수 있을 것 같다.

for(int i=0;i<N;i++){
	for(int j=Coin[i];j<=N;j++){
	    DP[i]+=DP[i-Coin[i]];
    }
} // i와 j의 범위는 그때그때 달라질 수 있음 (ex i=0이 아니라 1부터 시작)