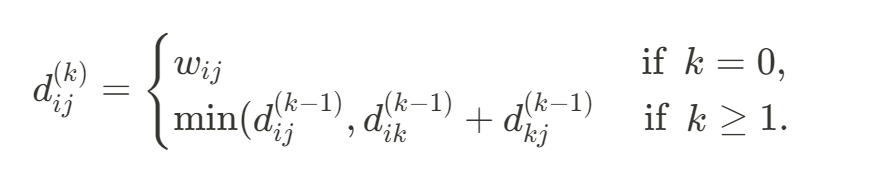[C++] 백준 1613 - 역사

문제 - 역사 (Gold3)

[백준 1613] https://www.acmicpc.net/problem/1613

Floyd-Warshall Algorithm

Floyd-Warshall algorithm은 원래는 그래프의 weight(거리)를 기준으로 최소 weight를 갖는 경로를 구하는 알고리즘이다. Dijkstra algorithm과 비슷해 보이지만, Floyd-Warshall algorithm은 거쳐가는 지점 k를 기준으로 하는 경로라는 점에서 차이점이 존재한다.

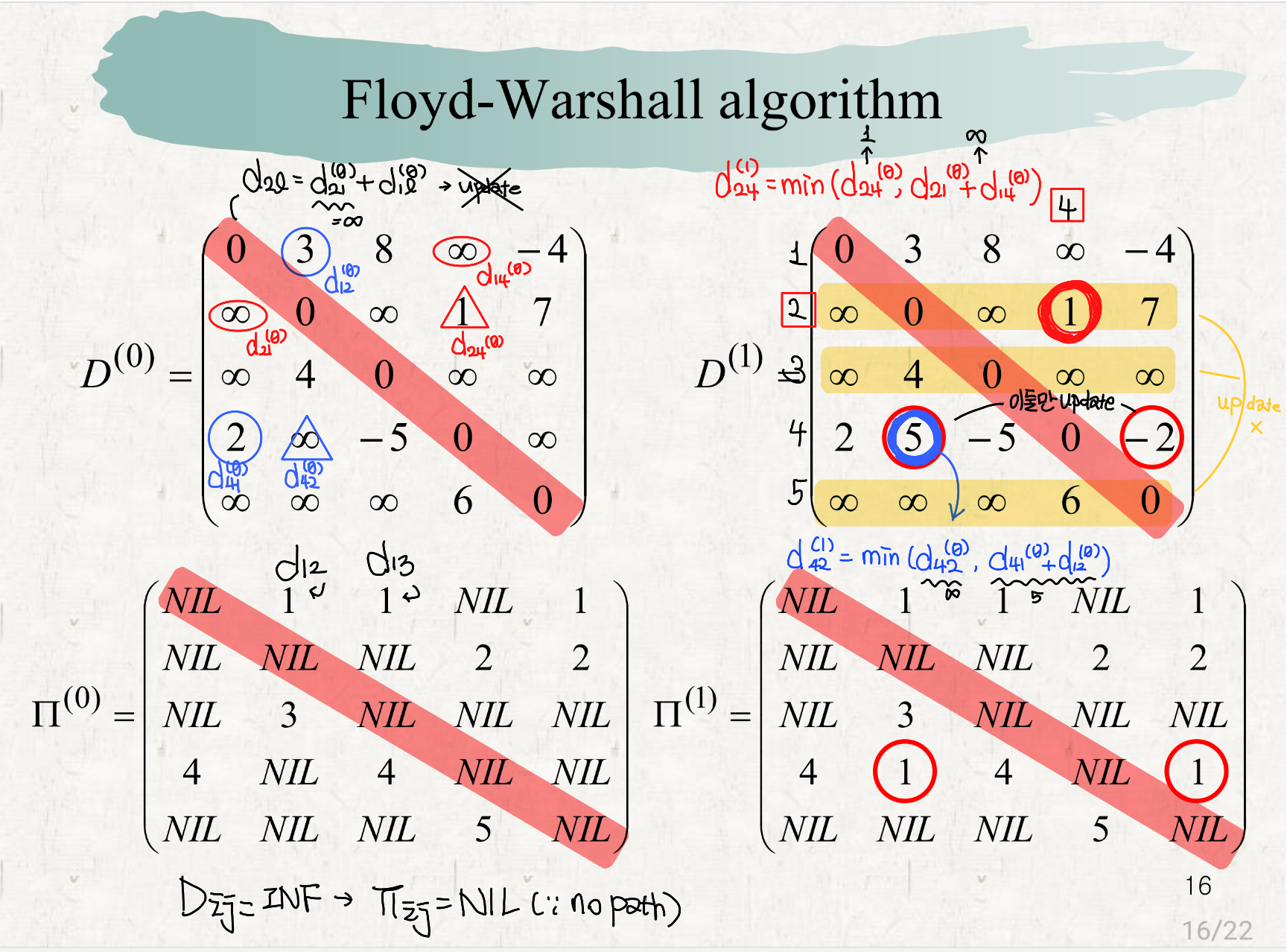
아래의 사진은 작년 2학기 '알고리즘 및 문제해결기법' 수업 시간에 배운 floyd-warshall 알고리즘의 필기 사진이다.

floyd-warshall 알고리즘의 경우, 점화식과 메인 알고리즘을 암기하면 쉽게 구할 수 있다.

• 점화식
  

• 메인 알고리즘

for(int k=0;k<N;k++){
	for(int i=0;i<N;i++){
    	for(int j=0;j<N;j++){
        	// i->j로 바로 가는 경로와 k를 거쳐서 가는 경로의 weight를 비교
        	D[i][j]=min(D[i][j], D[i][k]+D[k][j]);
        }
    }
}

풀이 전략

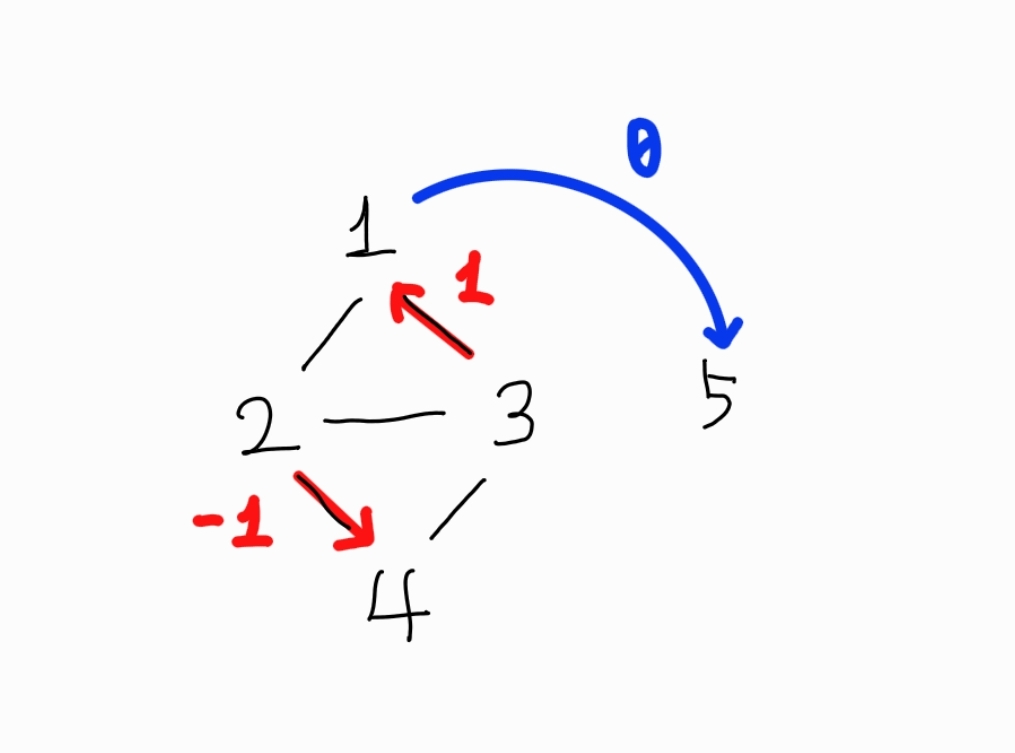
이 문제의 경우, 경로마다의 weight가 주어져 있지 않고 순서에 따라 -1,0,1로 구분해놓았기 때문에 weight를 -1,0,1로 보고 2차원 행렬을 만든 뒤, 조건문에 따라 출력을 하도록 구현할 것이다.

풀이

중간의 아래의 코드를 입력해서 이차원 배열 v에 들어가 있는 숫자를 확인해보면 다음과 같다.

for(int i=1;i<=K;i++){
	for(int j=1;j<=K;j++){
    	cout<<v[i][j]<<" ";
    }
    cout<<'\n';
}

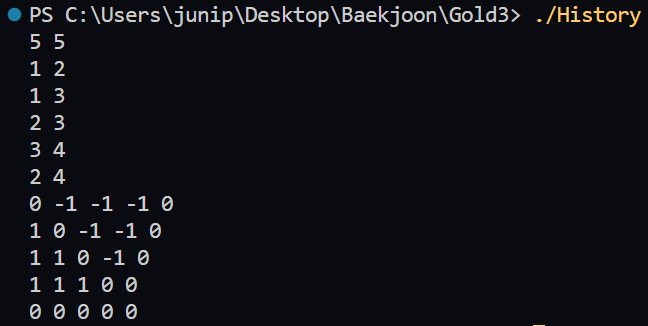
v배열이 대칭행렬이 되는데, 그 이유는 연도 순서와 관련이 있다.
그리고 5행과 5열이 0인 이유는 1,2,3,4와 연결된 edge가 없기 때문이다.

소스 코드

/*문제 : https://www.acmicpc.net/problem/1613
  알고리즘 : 그래프 이론, 최단 경로, 플로이드-워셜
  티어 : Gold3
*/
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N,K;
    cin>>N>>K;
    vector<vector<int>> v(N+1,vector<int>(N+1,0));

    for(int i=1;i<=K;i++){
        int s,e;
        cin>>s>>e;
        v[s][e]=-1;
        v[e][s]=1;
    } 
    // 임진왜란 -> 병자호란의 경우를 -1로 그 반대의 경우를 1로 저장

    for(int k=1;k<=N;k++){
        for(int i=1;i<=N;i++){
            for(int j=1;j<=N;j++){
                if(v[i][j]==0){
                    if(v[i][k]==1 && v[k][j]==1){
                        v[i][j]=1;
                    }
                    else if(v[i][k]==-1 && v[k][j]==-1){
                        v[i][j]=-1;
                    }
                } // i-> j로 바로 가는 경로는 없는데 k를 거쳐서 가는 경로는 있는 경우
            }
        }
    }

    int S;
    cin>>S;

    for(int i=1;i<=S;i++){
        int a,b;
        cin>>a>>b;
        cout<<v[a][b]<<"\n";
    }
    return 0;
}

결과

결론

플로이드 와샬 알고리즘을 weight에만 한정하지 않고 여러 방면으로 써볼 수 있는 좋은 문제인 것 같다.