RB 트리 -1

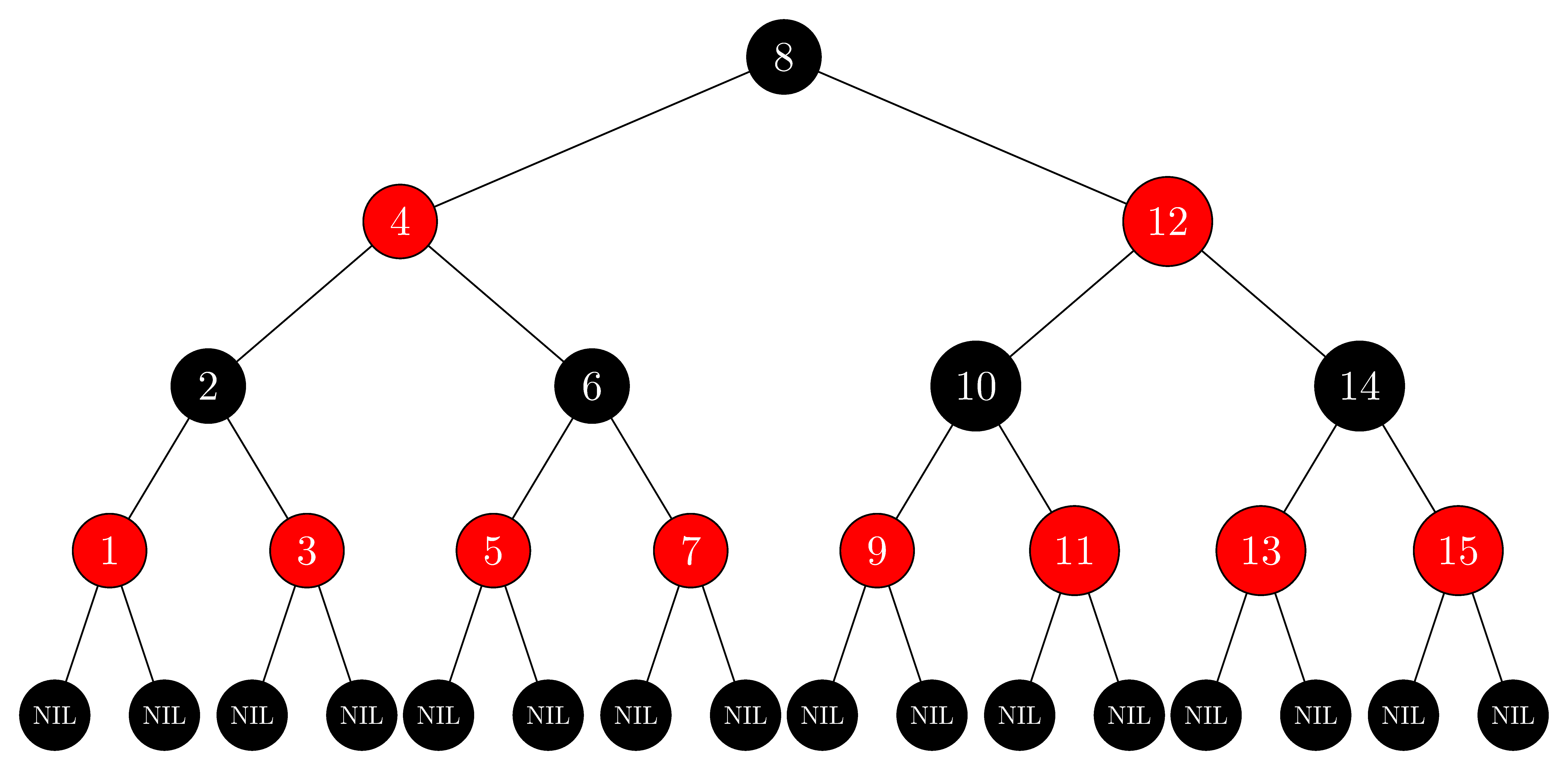
레드 블랙 트리 (Red-Black Tree)

• 이진 탐색 트리(BST)의 한 종류
• 스스로 균형(balancing) 잡는 트리 O(logN)
• BST 의 worst case의 단점을 개선
  • 한쪽으로 편향되어있는 상태의 삽입 삭제 검색의 시작 복잡도 O(N) = 모든 노드를 한번씩 확인해야 함

---

속성

1. 모든 노드는 Red 혹은 Black

2. 루트 노드는 Black

3. 모든 nill(leaf)노드는 Black

4. Red 의 자녀들은 Black ( = Red 는 연속적으로 존재할 수 없다 )

5. 임의의 노드에서 자손 nill 노드들까지 가는 경로들의 Black 수는 같다 ( 자기 자신은 카운트에서 제외 )

5a. 노드 x의 Black height

• 노드 x에서 임의의 자손 nil 노드까지 내려가는 경로에서의 black 의 개수 (자기 자신 제외)
• 5번 속성을 만족할때만 해당 개념 성립

5b. 색 바꾸기

• RB 트리가 5번 속성을 만족한다면,
• 두 자녀가 같은 색을 가질 때, 부모와 두 자녀의 색을 바꿔도 5번 속성은 여전히 만족

📌 plus : Nil 노드

• 존재하지 않음을 의미하는 노드
• 자녀가 없을 때 자녀를 nill 노드로 표기
• 값이 있는 노드와 등등하게 취급
• RB 트리에서 모든 nill 노드는 leaf 노드(자녀X) 이다

---

균형 잡기

• 삽입/삭제 시 주로 #4, #5를 위반해서 이들을 해결하려고 구조를 바꾸다보면, 자연스럽게 트리의 균형이 잡히게 된다.

---

시간 복잡도

• N : 트리의 노드 수

	AVG	Worst
Insert	O(logN)	O(logN)
Delete	O(logN)	O(logN)
Search	O(logN)	O(logN)

---

RD tree 와 AVL tree 비교

• N : 트리의 노드 수

	RB	AVL
Binary Search Tree	Yes	Yes
삽입/삭제/검색 시간 복잡도	wort case 에서도 O(longN)	wort case 에서도 O(longN)
삽입/삭제 성능	AVL 트리에 비해 빠름	RB 트리에 비해 느림
검색 성능	AVL 트리에 비해 느림	RB 트리에 비해 빠름
균형 잡는 방식	RB 트리 속성을 만족시키도록	balance factor ∈ {-1, 0, 1} 되도록
응용 사례	linux kernel 내부에서 사용,	dictionary, 한번 만들어 놓으면 삽입/삭제가
	c++std::map 구현, etc...	거의 없고 검색이 대부분인 상황에서 사용

>> AVL 트리 알아보기