삽입 방식
- 삽입 전 RB 트리 속성을 만족한 상태
- 일반적인 BST의 삽입 방식과 동일
- 삽입 후 RB 트리 위반 여부 확인
- RB 트리 속성을 위반했다면 재조정
- RB 트리 속성을 다시 만족
레드 블랙트리의 속성 복습하기!
속성
- 루트 노드는 Black
⭐ 4. Red 의 자녀들은 Black ( = Red 는 연속적으로 존재할 수 없다 )
⭐ 5. 임의의 노드에서 자손 nill 노드들까지 가는 경로들의 Black 수는 같다 ( 자기 자신은 카운트에서 제외 )
- 삽입 노드의 색은 항상 Red 이다. (nil 노드 2개도 함께 따라옴)
-
Red 삽입 후
#2 속성(루트=Black) 을 위반-
해결 : 루트 노드를 Black 으로 바꿔주기
-
Red 를 삽입하는 이유 : 삽입 후에도
#5 속성을 만족시키기 위해
ex) Red 노드 삽입 후에는 조상 노드부터 nill 노드까지의 경로의 black 수는 같다
-
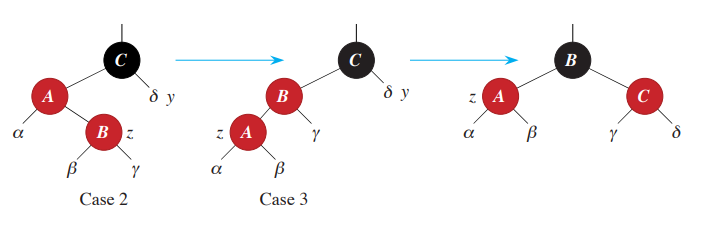
CASE 3.
: Red 삽입 후 #4 속성 (Red 자녀 = Black) 을 위반
- 형태 : Red 가 몰려있다!
- 삽입된 노드 = 부모의 왼쪽 자녀 &
- 부모 = red, 할아버지 왼쪽자녀 &
- 부모 형제 = black
( 왼쪽/오른쪽 바꿔도 성립 ) - 해결 : 위반한 노드를 반대편으로 옮겨주기
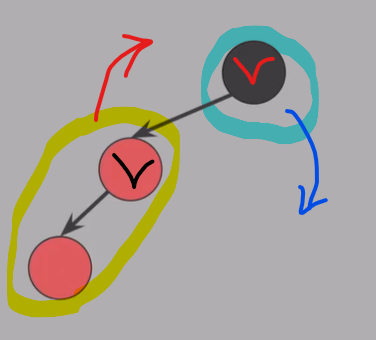
- BST 특징도 유지하면서 삽입한 Red 을 넘기기 위해 [ 회전 ] 을 사용해야 함
- 할아버지와 부모의 색을 먼저 바꿔주기 (회전 후에도
#5속성 유지됨) - 부모를 기준으로 회전! (왼쪽삽입->오른쪽 회전)
CASE 2.
: Red 삽입 후 #4 속성 (Red 자녀 = Black) 을 위반
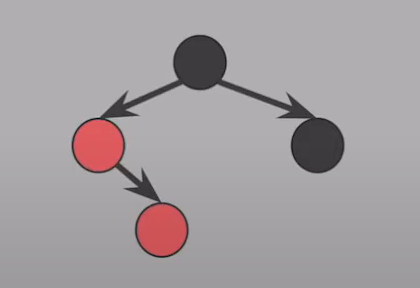
- 형태 : Red 가 꺾여 있다!
- 삽입된 노드 = 부모의 오른쪽 자녀 &
- 부모 = red, 할아버지 왼쪽자녀 &
- 부모 형제 = black
( 왼쪽/오른쪽 바꿔도 성립 ) - 해결 :
Case 3형태로 만들어주기
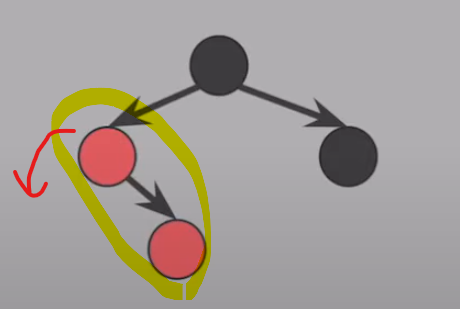
- 부모를 기준으로 [ 회전 ] 한 후
Case 3와 같은 방식으로 해결
- 부모를 기준으로 [ 회전 ] 한 후
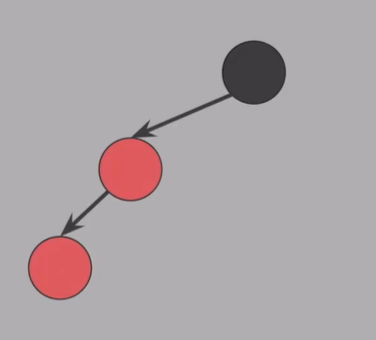
CASE 1.
: Red 삽입 후 #4 속성 (Red 자녀 = Black) 을 위반
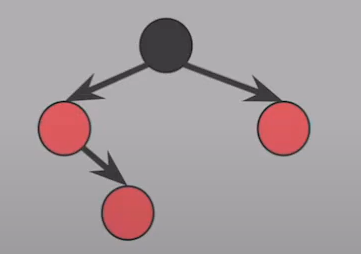
-
형태 : Red 가 몰려있다!
- 삽입된 노드의 위치는 상관없음
- 부모 = red
- 부모 형제 = red
( 왼쪽/오른쪽 바꿔도 성립 ) -
해결 : 위반한 노드를 반대편으로 옮겨주기
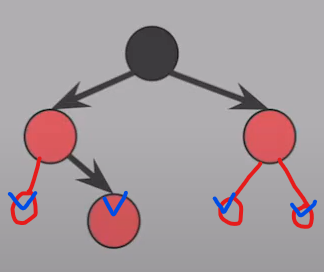
- 부모와 부모의 형제를 Black으로 바꾸기
- 할아버지 색을 Red 로 바꾸기
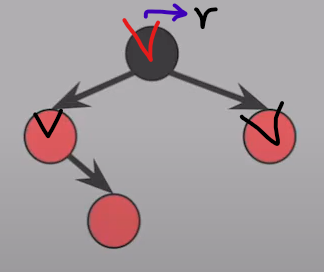
- 할아버지부터 다시 확인 시작하기
ex) 만약 할아버지(=루트)가#2 속성을 위반했다면 루트노드를 Black으로 바꾸기
ex) 할아버지의 부모노드가 있을 수 있다.
📌 plus : 회전
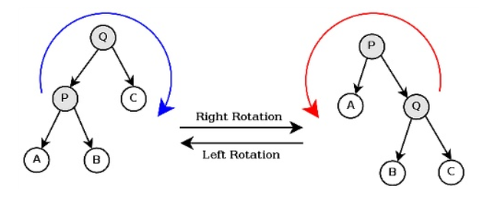
<예시> : M을 기준으로 우회전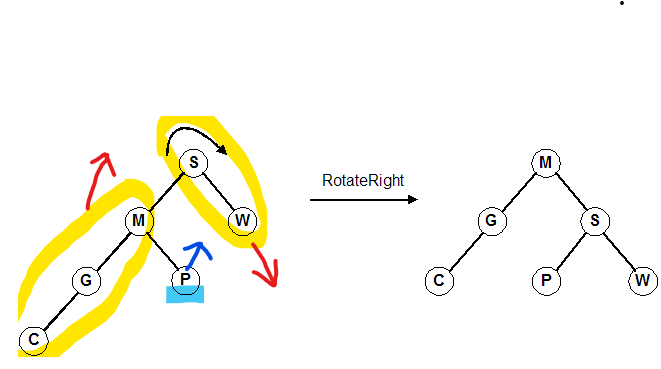
M은 왼쪽 서브트리와 함께 위로 올라감S의 오른쪽 서브트리는 밑으로 내려감.M의 오른쪽 서브트리가S의 왼쪽 서브트리가 된다.
