[ML Project] 로지스틱 회귀를 이용한 날씨 예측

💻 프로젝트 설명

• kaggle의 호주의 날씨 관련 데이터셋을 이용하여 로지스틱 회귀 모델을 학습시킨 후 날씨를 예측해보았다.

[데이터셋 링크] https://www.kaggle.com/datasets/jsphyg/weather-dataset-rattle-package?select=weatherAUS.csv

📁 데이터셋

[구성]

• Date: 날짜
• Location: 위치
• MinTemp: 최저기온
• MaxTemp: 최고기온
• Rainfall: 강수량
• Evaporation: 증발량
• Sunshine: 일조시간
• WindGustDir: 24시간에서 자정까지 가장 강한 돌풍의 방향
• WindGustSpeed: 24시간에서 자정까지 가장 강한 돌풍의 속도(km/h)
• WindDir9am: 오전 9시 바람의 방향
• WindDir3pm: 오후 3시 바람의 방향
• WindSpeed9am: 오전 9시 바람 속도
• WindSpeed3pm: 오후 3시 바람 속도
• Humidity9am: 오전 9시 습도
• Humidity3pm: 오후 3시 습도
• Pressure9am: 오전 9시 기압
• Pressure3pm: 오후 3시 기압
• Cloud9am: 오전 9시에 구름에 가려진 하늘의 일부분
• Cloud3pm: 오후 3시에 구름에 가려진 하늘의 일부분
• Temp9am: 오전 9시 기온
• Temp3pm: 오후 3시 기온
• RainToday: 오늘 비의 양(mm)

[EDA]

• 가장 먼저 결측치를 확인해보았는데 116368열 중 결측치가 많은 항목은 결측치가 5만개가 넘게 있었다.
  

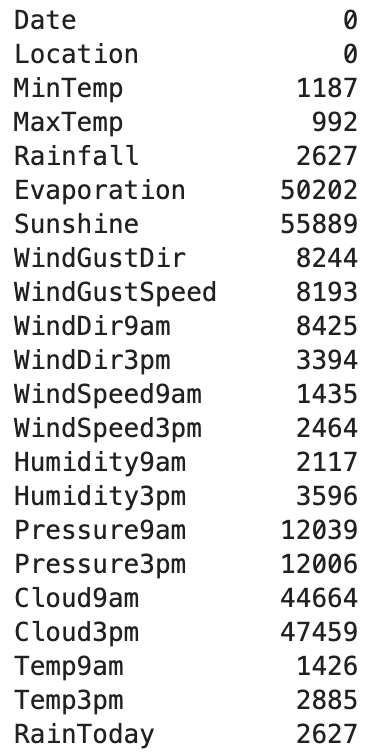
• 상관계수를 히트맵으로 나타내었을때는 예상하지 못한 인사이트를 주는 항목은 없었다.
  

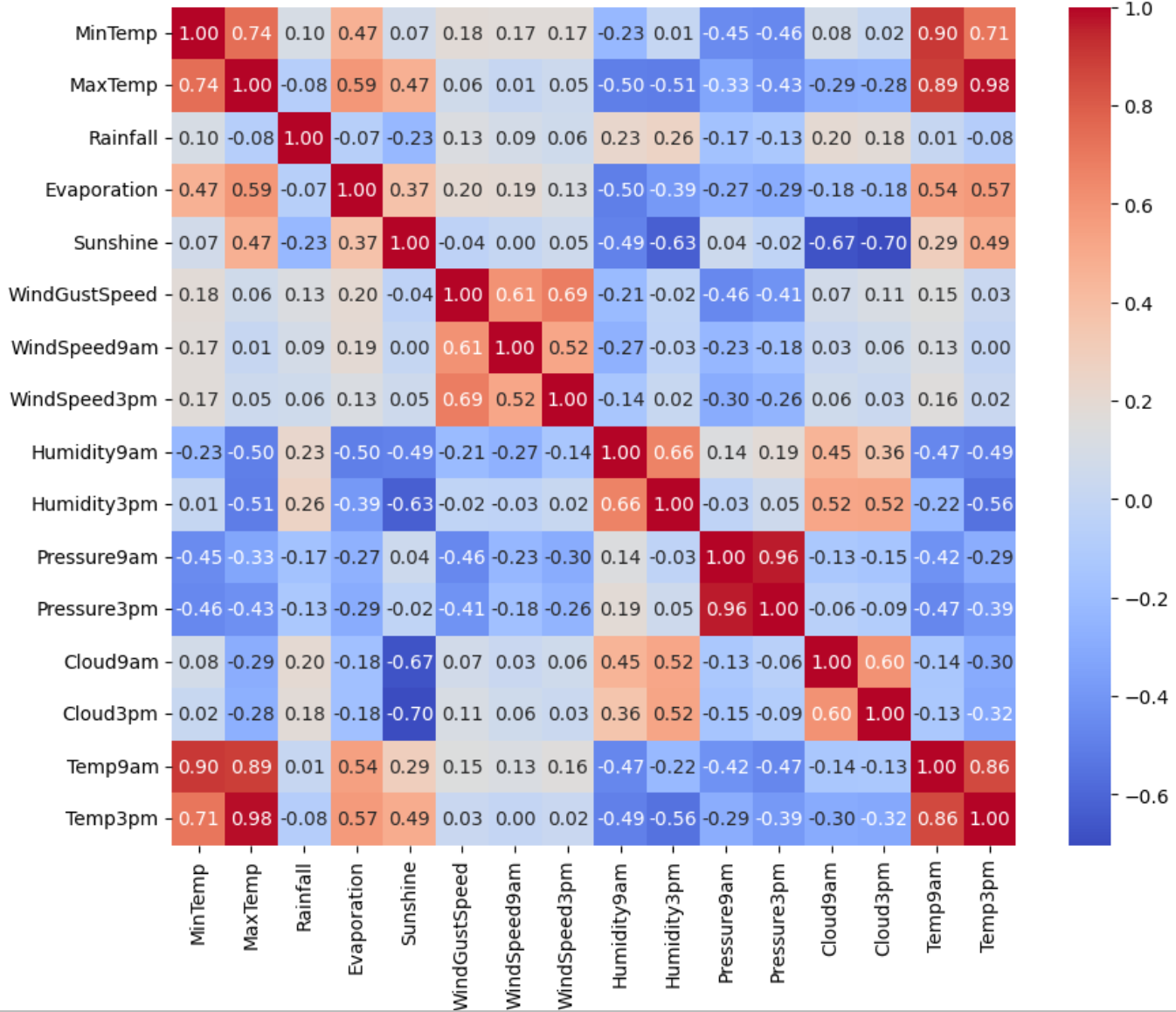
• 오늘 비가 왔을 때 다음날 비가 오지 않은 횟수가 더 많았고, 오늘 비가 오지 않았을 때 다음날 비가 오지 않은 횟수가 월등하게 많았다.

[All]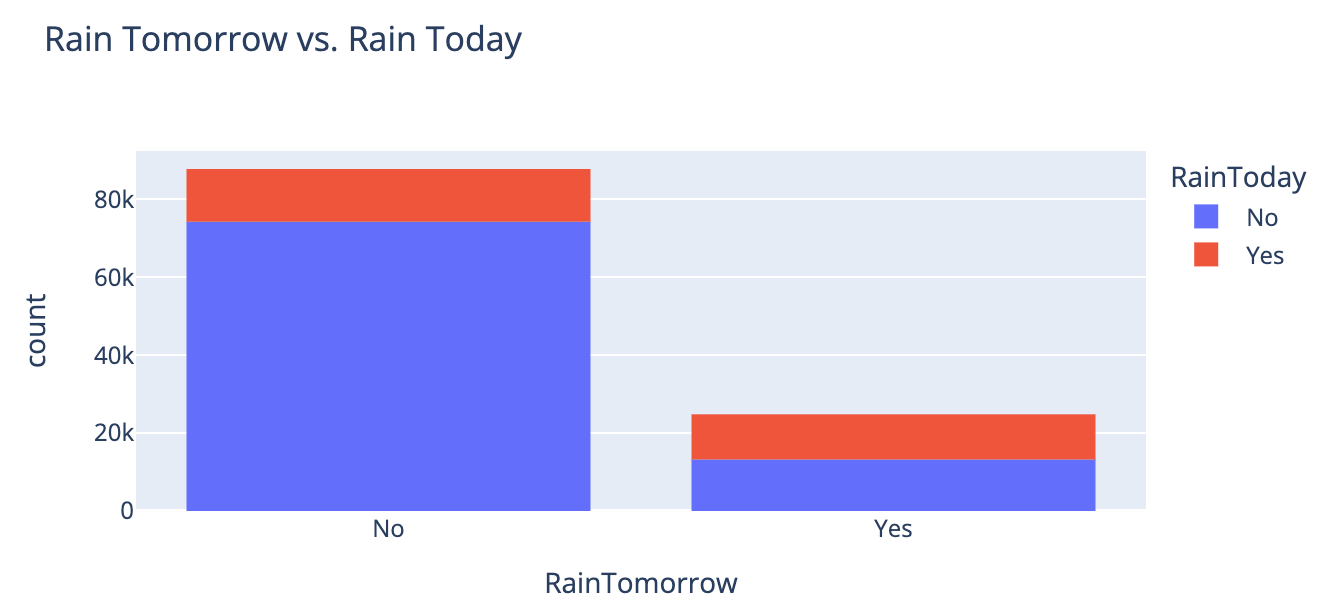	[Today-Yes]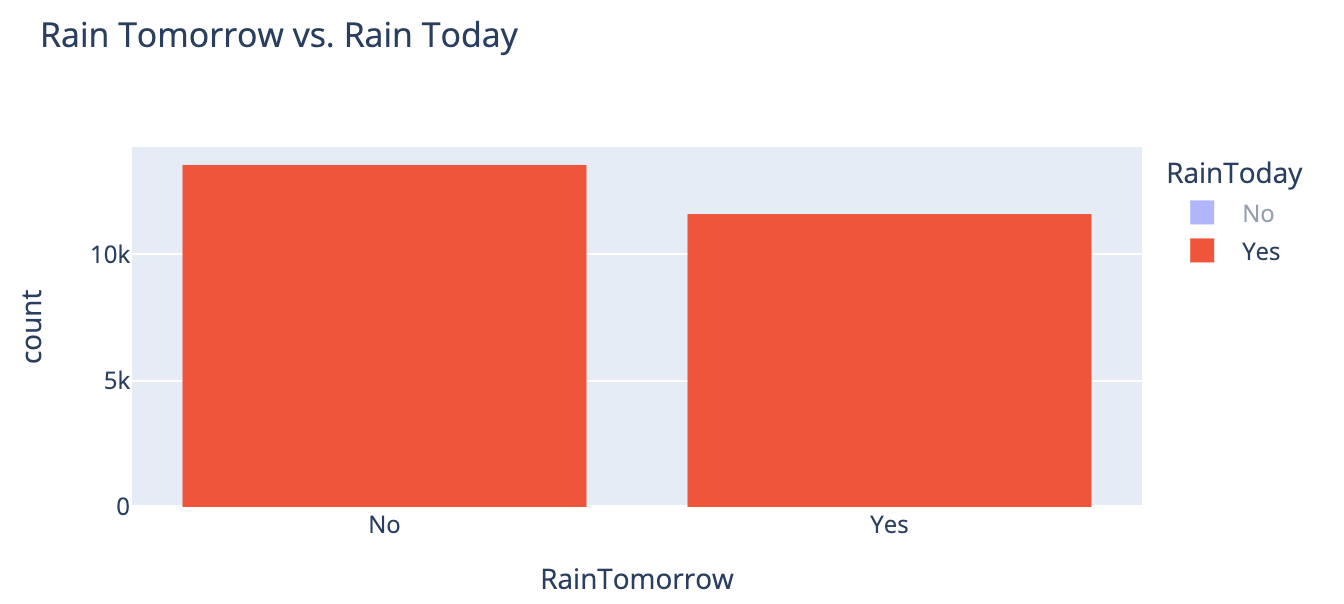	[Today-No]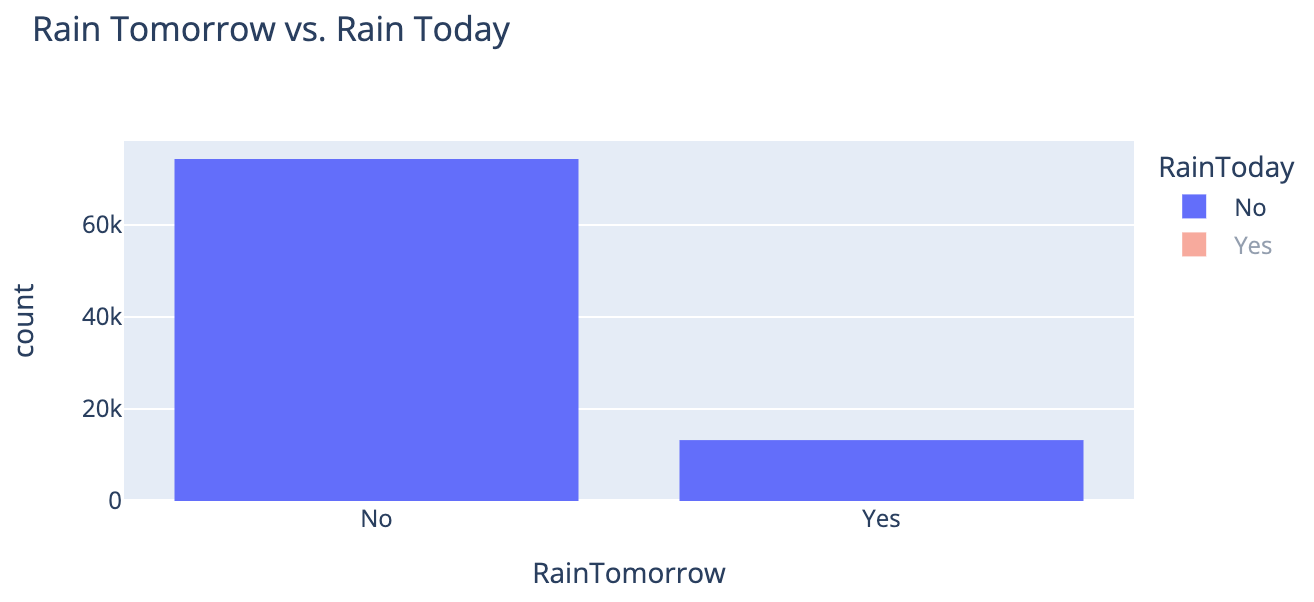

• 지역별로 비가 온 날의 평균을 그래프로 그려보았다.
  이 그래프를 통해 강수량이 지역에 따라 영향을 받는 것을 알 수 있다.

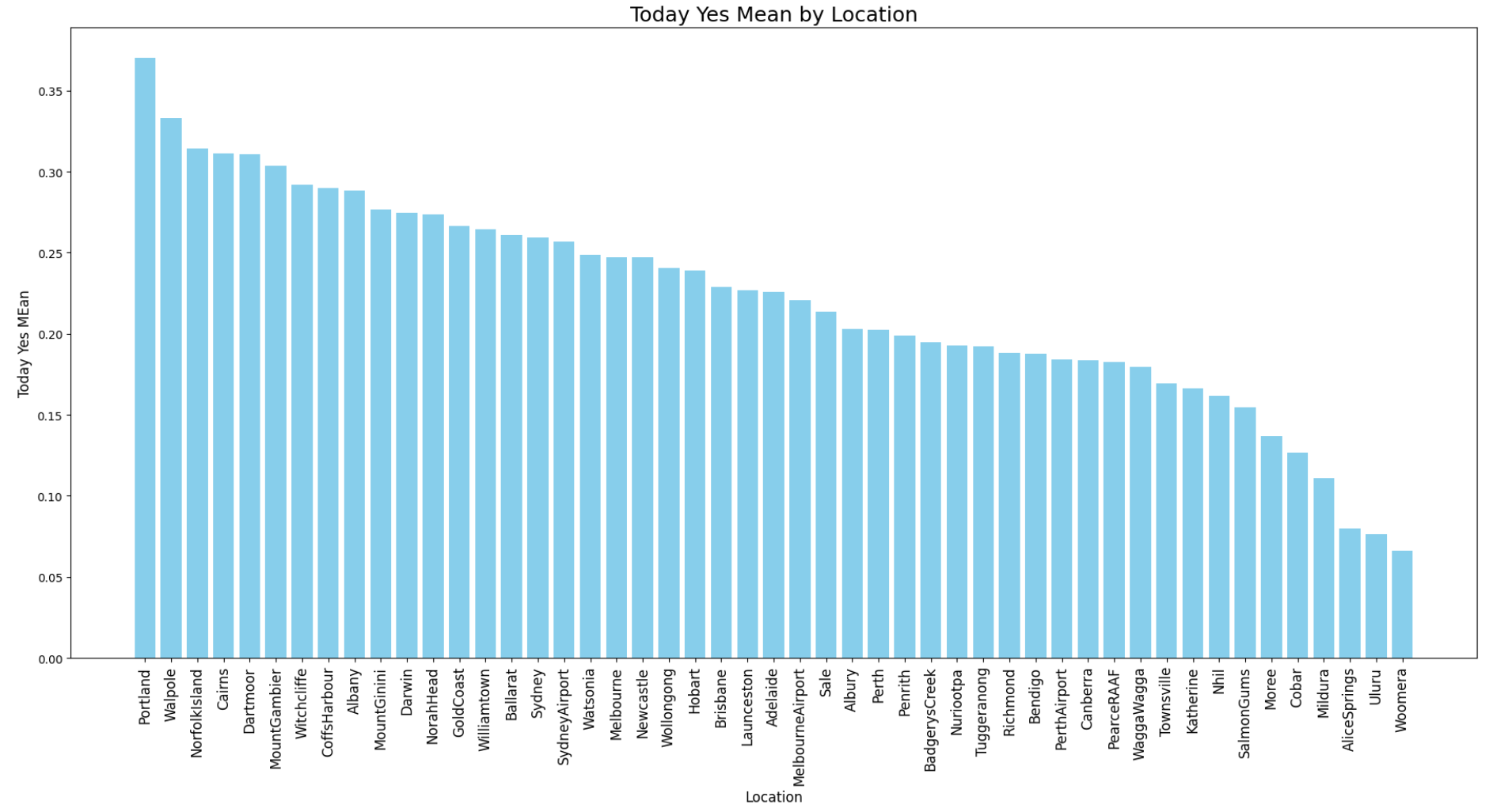
• 강수량 평균 Top 10과 Low 10을 따로 그려보았다.
  특히 Low 10에 속한 지역들을 살펴보면 호주 내륙쪽의 사막 지역임을 알 수 있다.

[Top 10]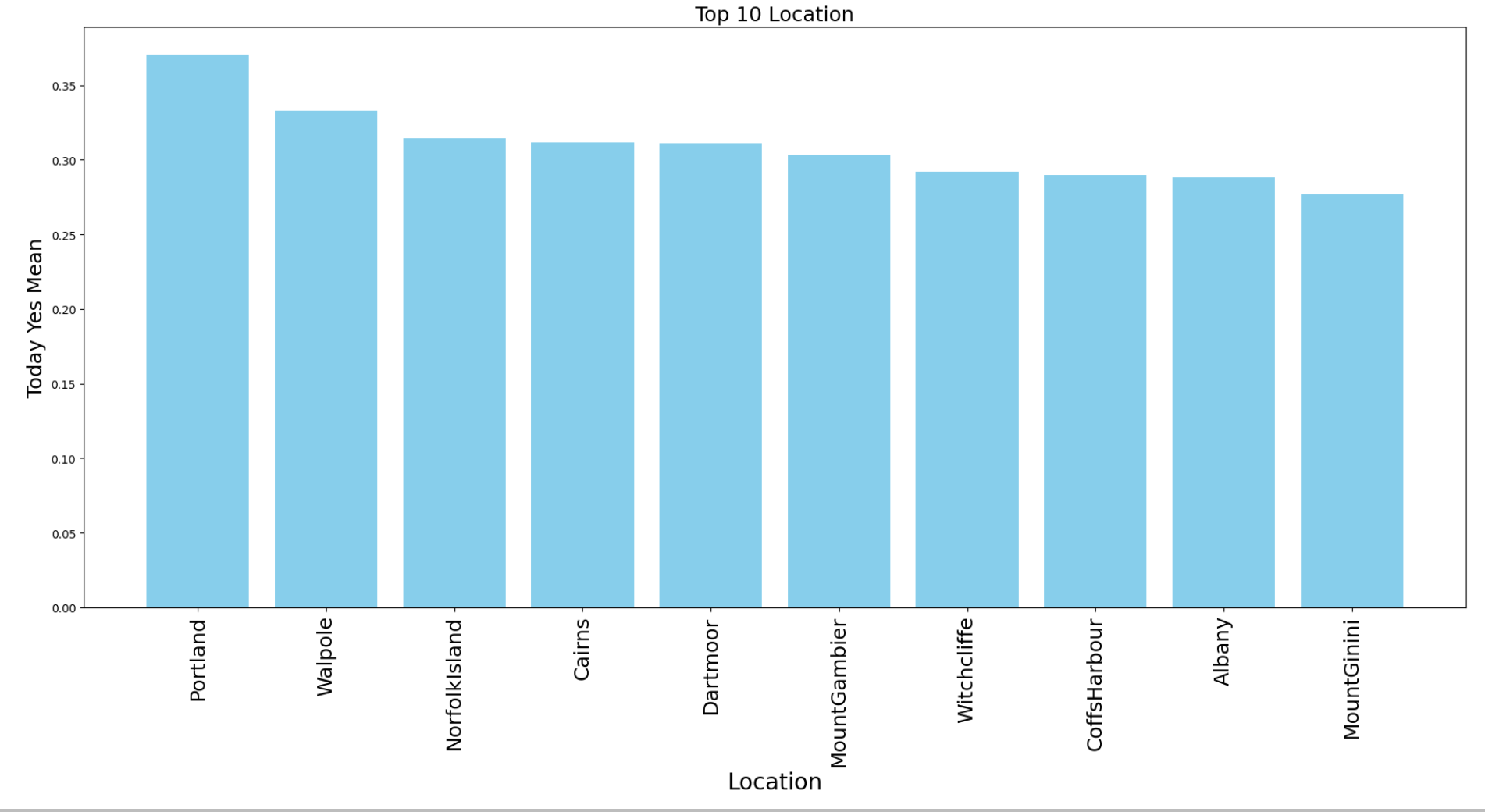	[Low 10]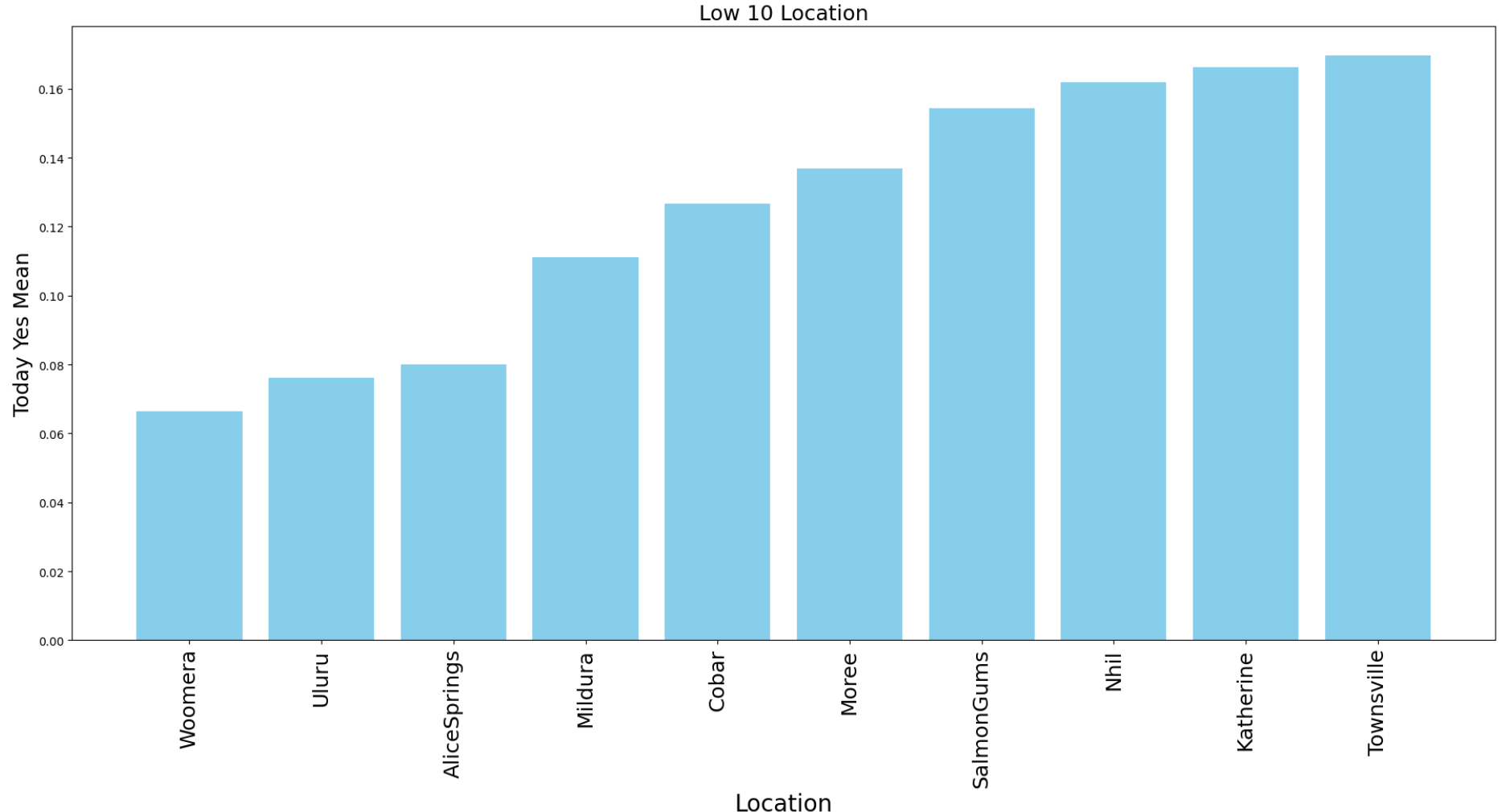

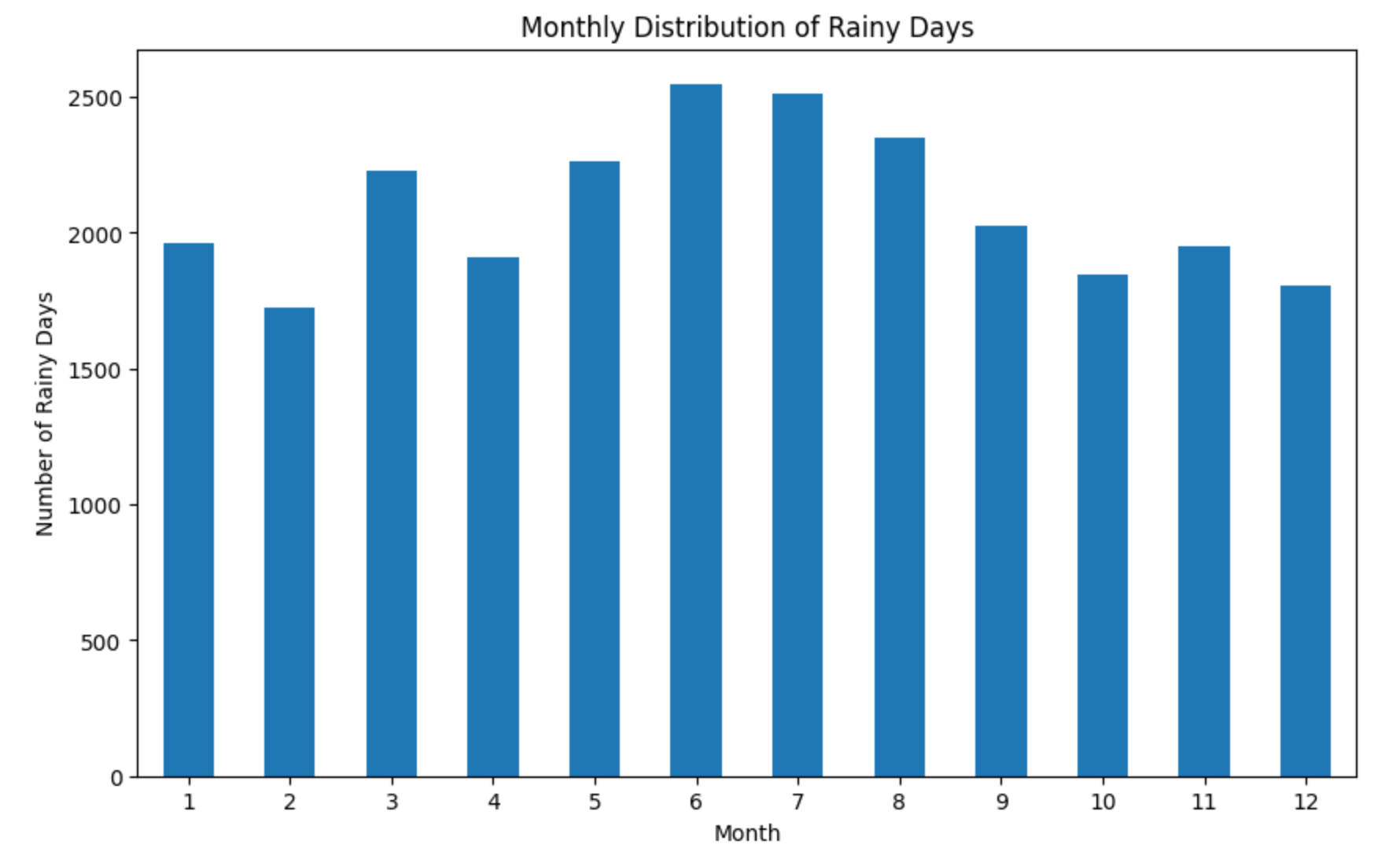
• 월별로 비가 온 날을 그래프로 그려보았다.
  비가 온 날은 6월이 가장 많았고, 2월이 가장 낮았다.

[전처리]

• 로지스틱 회귀에서 x_train & y_train 그리고 x_test & y_test은 행의 수가 같아야 하고, 결측치가 전체 데이터의 약 2-3%밖에 존재하지 않기 때문에 결측치가 있는 행은 drop했다.

[x_train]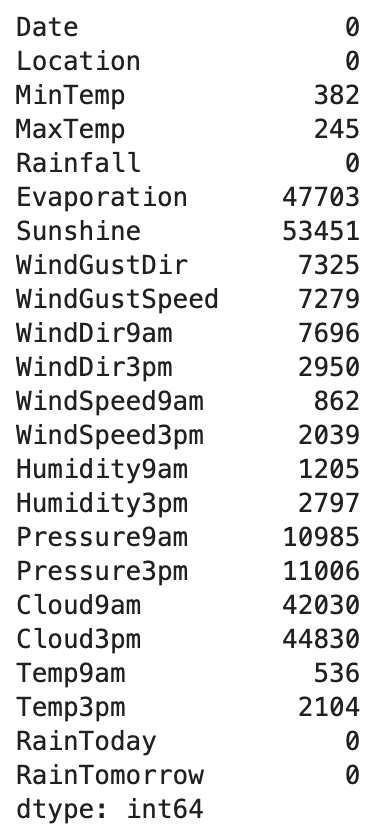	[x_test]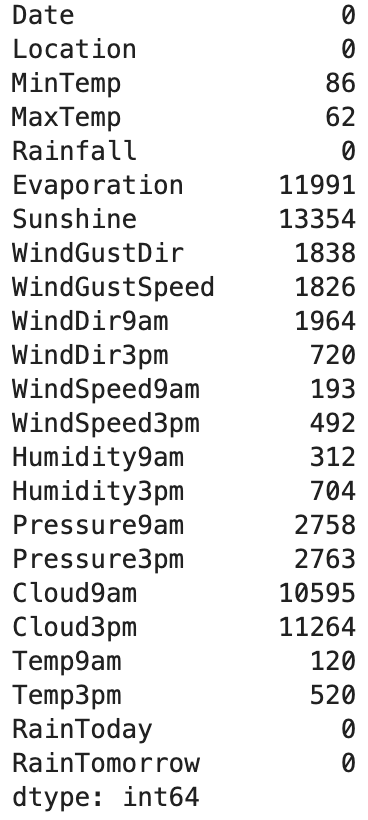

• 수치형 칼럼의 결측치는 평균으로 대체해주었다.

[x_train]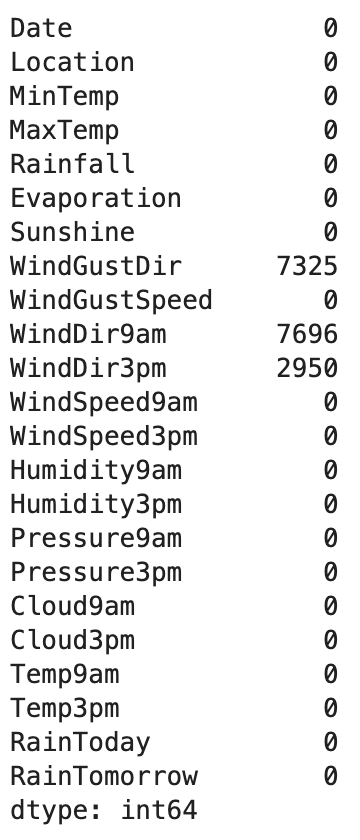	[x_test]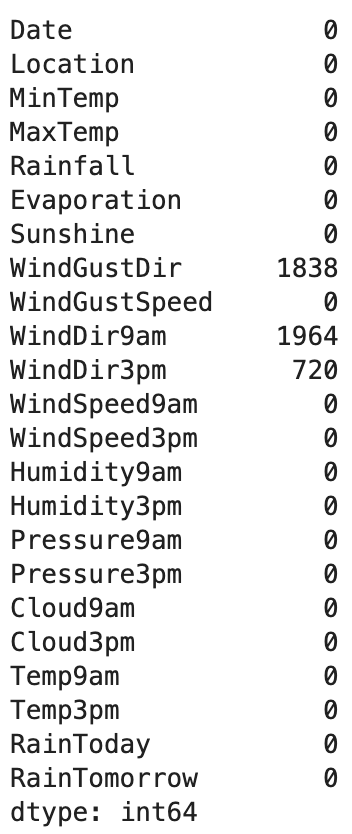

• 범주형 카테고리는 최빈값을 넣어 결측치를 대체해주었다.

[x_train]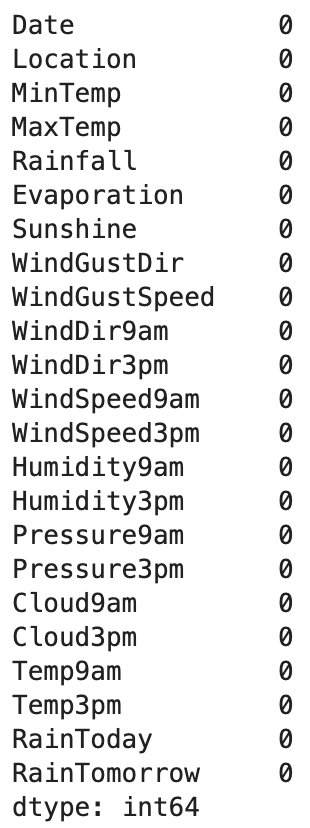	[x_test]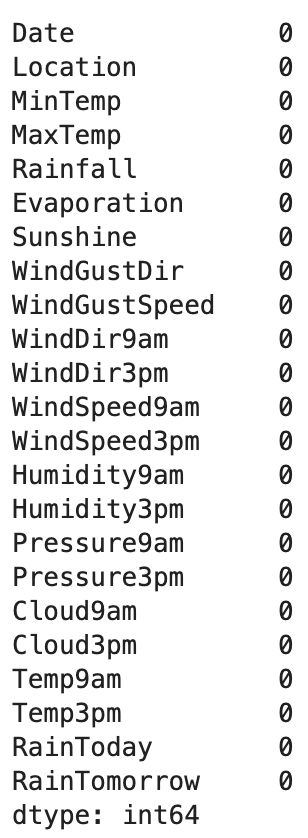

• 수치형 데이터는 정규화를 해주었다.

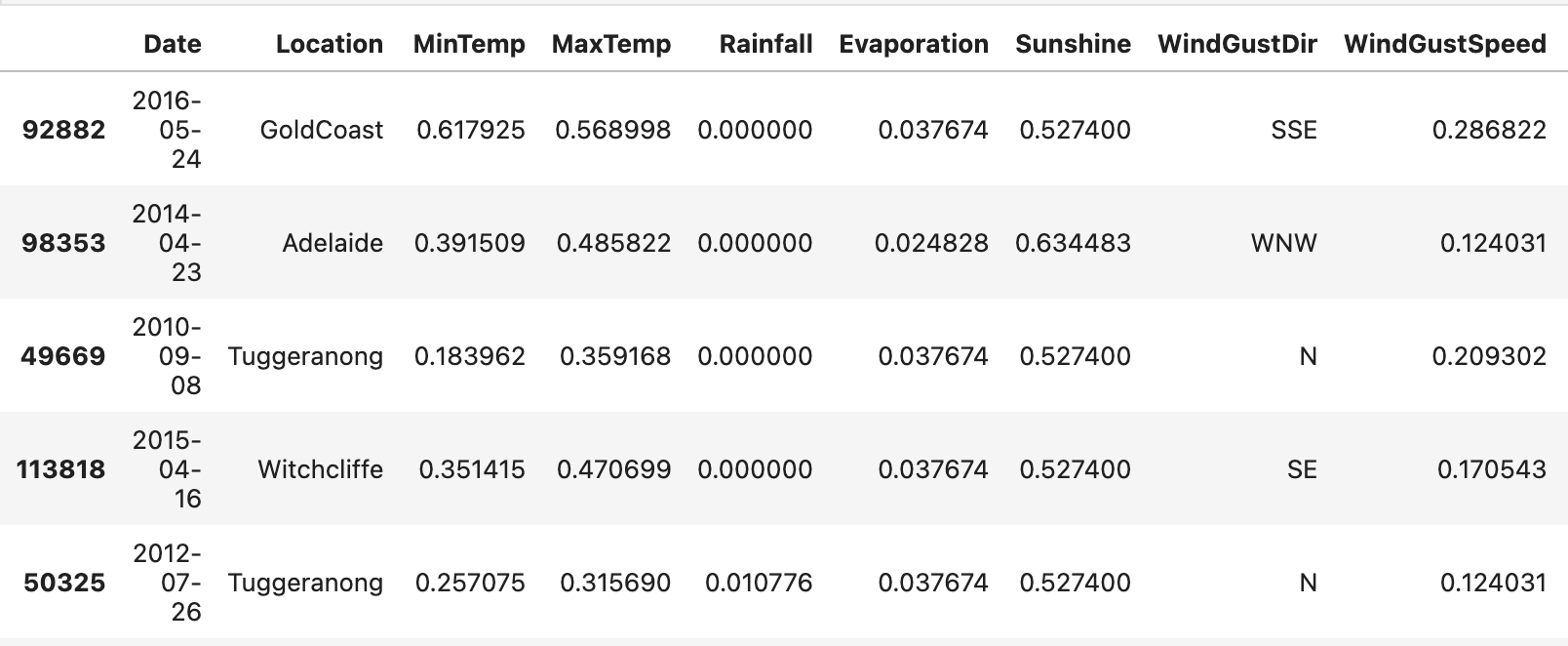
• RainToday를 제외한 범주형 데이터는 원핫인코딩을 해주었고, RainToday와 RainTomorrow는 라벨인코딩을 해주었다.
  또한 강수량에 월 정보도 영향을 미친다고 보고 Date에서 월 데이터를 뽑아 Month 칼럼을 만들어 준 후 원-핫 인코딩을 해주었다.

[Encoding]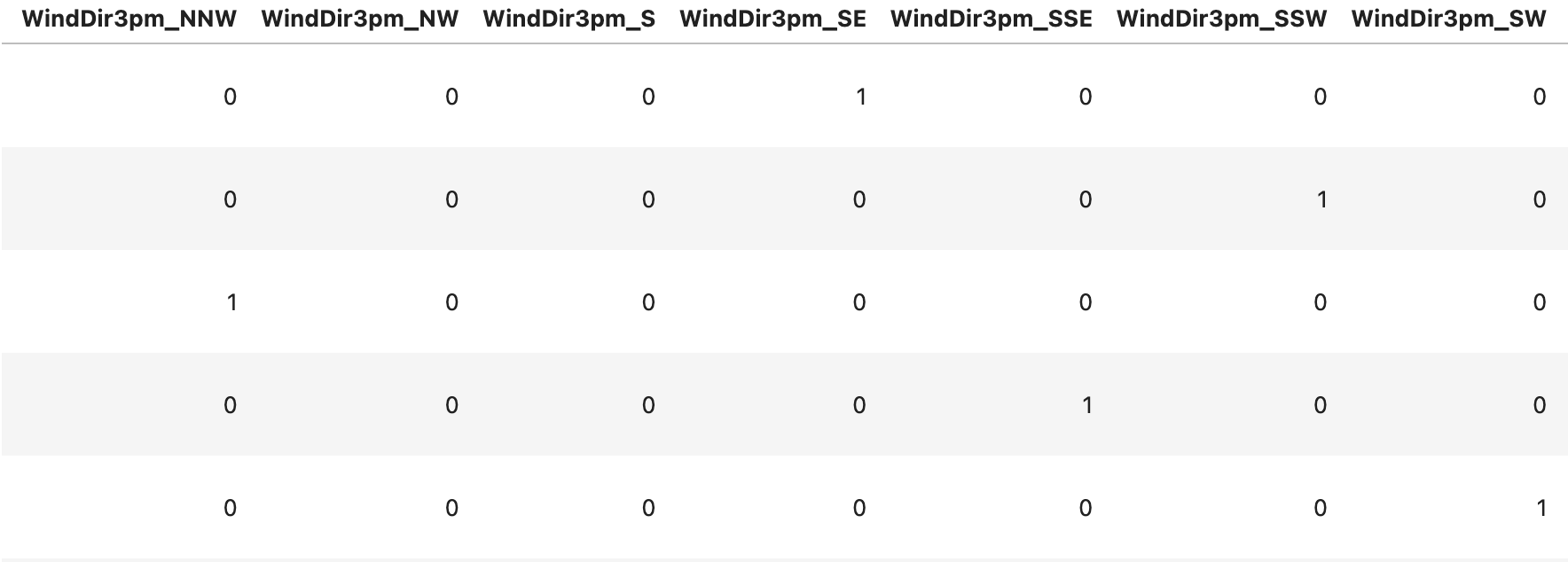	[Month Encoding]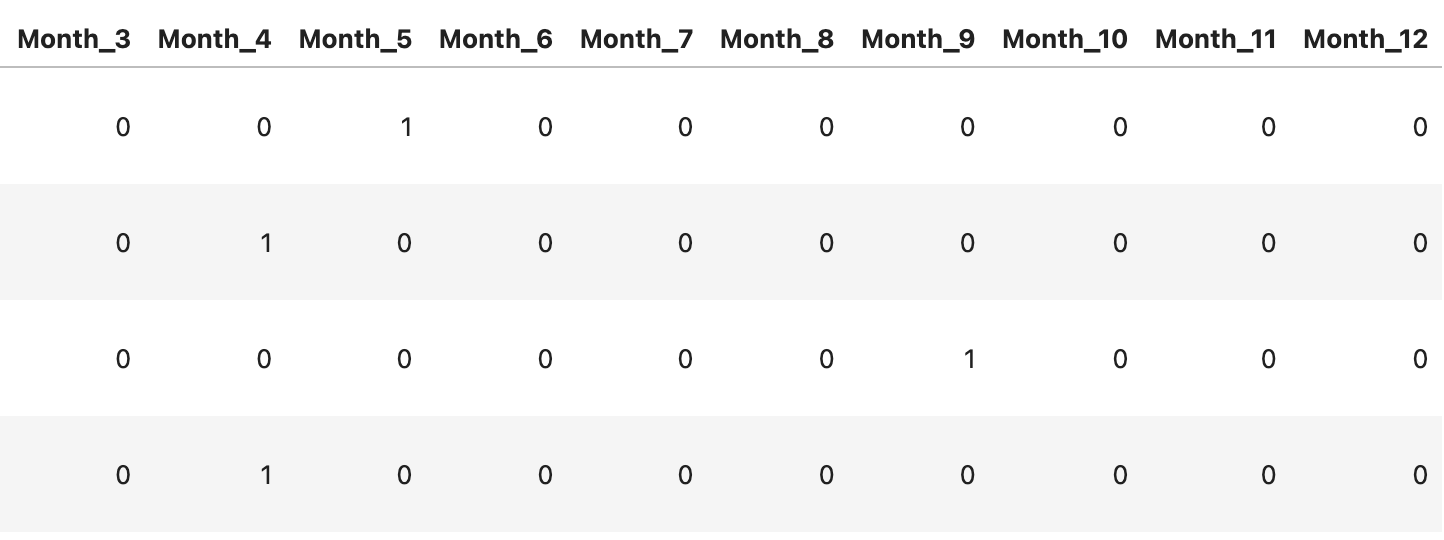	[Label Encoding]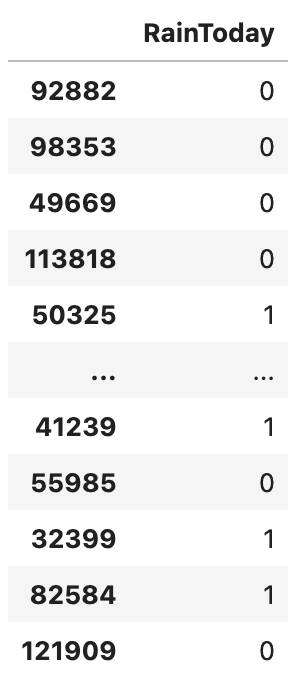

📈 로지스틱 회귀

• 로지스틱 회귀 결과를 보면 아래와 같다.

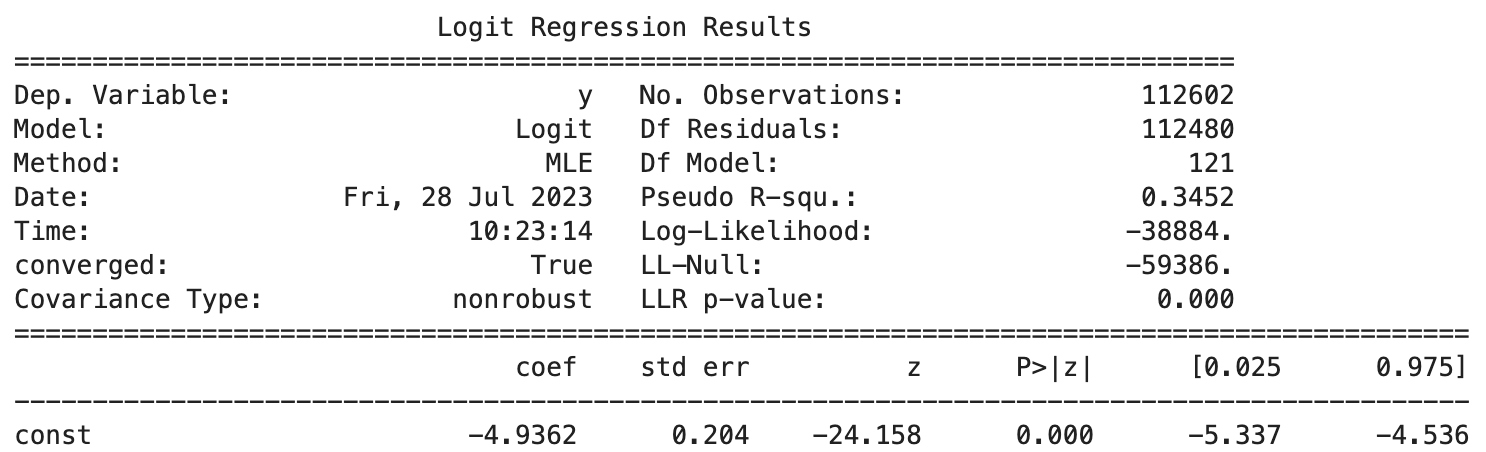
-> Pseudo R-squ.(의사결정계수): 모델이 데이터에 얼마나 잘 맞는지 측정하는 척도로, 선형 회귀의 R-제곱과 유사하다. 값은 0에서 1 사이이며, 0은 모델이 변동을 전혀 설명하지 못함을 의미하고 1은 모델이 변동을 완벽하게 설명함을 의미한다.
이때 내가 학습시킨 모델은 수치가 0.35로 낮게 나와 검색해보니, 로지스틱 회귀분석에서 해당 값은 대개 낮게 나오는 편이므로 모델 평가에서 의사결정계수에 너무 의존할 필요는 없고 한다.

-> Log-Likelihood(로그 우도): 최적화된 솔루션의 로그 확률 값으로 모델이 데이터에 얼마나 잘 맞는지를 나타낸다. 절대 로그 확률 값이 높을수록 값이 양수인지 음수인지에 관계없이 데이터에 더 잘 맞는다는 것을 의미한다.
위 모델은 절대값이 매우 크기때문에 모델이 데이터에 적합함을 알 수 있다.

-> L-Null & LLR p-value: L-Null은 Null 모델의 적합도에 대한 정보를 제공하는 반면, LLR p값은 더 복잡한 모델에 예측자를 추가하면 Null 모델에 비해 모델의 적합도가 크게 향상되는지 여부를 테스트한다. 일반적으로 L-Null 값이 더 음수일수록 LLR p값이 0에 가까울수록 모델이 데이터에 더 잘 맞고 예측자의 중요도가 높다는 것을 나타낸다.
위 모델에서는 L-Null가 매우 큰 음수값이고, LLR p-value가 0에 가깝기 때문에 모델이 데이터에 적합함을 알 수 있다.

[분류 모델 성능 평가]

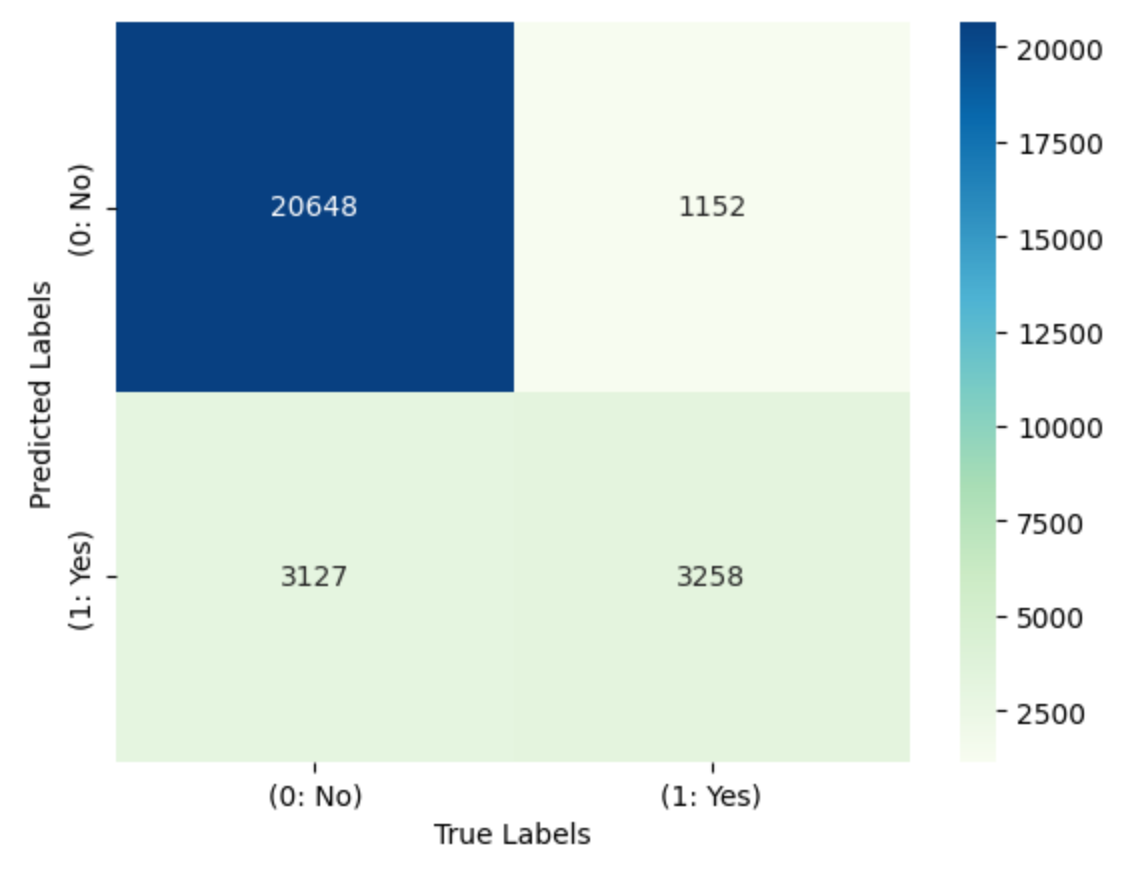
• Confusion Matrix를 그려보았다.
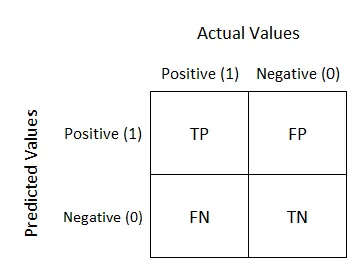
  아래 표는 그림이 나타내는 라벨을 표로 만든 것이다.
  TN: Negative로 예측했으나 실제로 Negative
  FN: Negative로 예측했으나 실제로 Positive
  FP: Positive로 예측했으나 실제로 Negative
  TP: Positive로 예측했으나 실제로 Positive

• train-set과 test-set의 정확도를 확인해보니 둘 다 높은 수치를 보였다.

  • 정확도: (TP+TN)/(TP+TN+FP+FN)
    
    -> 정확도: 전체 중에 예측과 결과가 같을 확률이다.

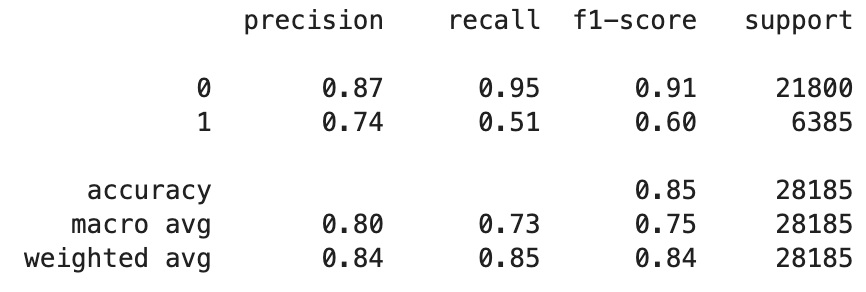
• 정밀도, 재현율, f1 score를 확인해보았다.

  • 정밀도(precision): (TP)/(TP+FP)
  • 재현율(recall): (TP)/(TP+FN)
  • f1 score: 2(정밀도 * 재현율)/정밀도+재현율
    
    -> 정밀도: Positive로 예측한것 중에 실제로 Positive인 비율로 False Positive(거짓 양성)를 최소화해야 하는 상황에서 중요하다.
    -> 재현율(=민감도): 실제 Positive인 중에 예측도 Positive로 한 비율로 False Negative(거짓 음성)를 최소화해야 하는 상황에서 중요하다.
    -> f1-score: 모델이 양성과 음성을 모두 정확하게 처리하는데 중점을 둘 때 F1 스코어를 사용하는 것이 적절하다.

• 이 모델은 클래스 0(아니오)을 예측할 때 높은 정확도와 재응답률로 우수한 성능을 보이는 것으로 보이나 반대의 경우 상대적으로 성능이 낮았다.
  즉, 실제 비가 오지 않을 때 비가 올거라고 잘못 예측할 확률은 낮으나 그 반대의 경우는 잘못 예측할 확률이 높았다.

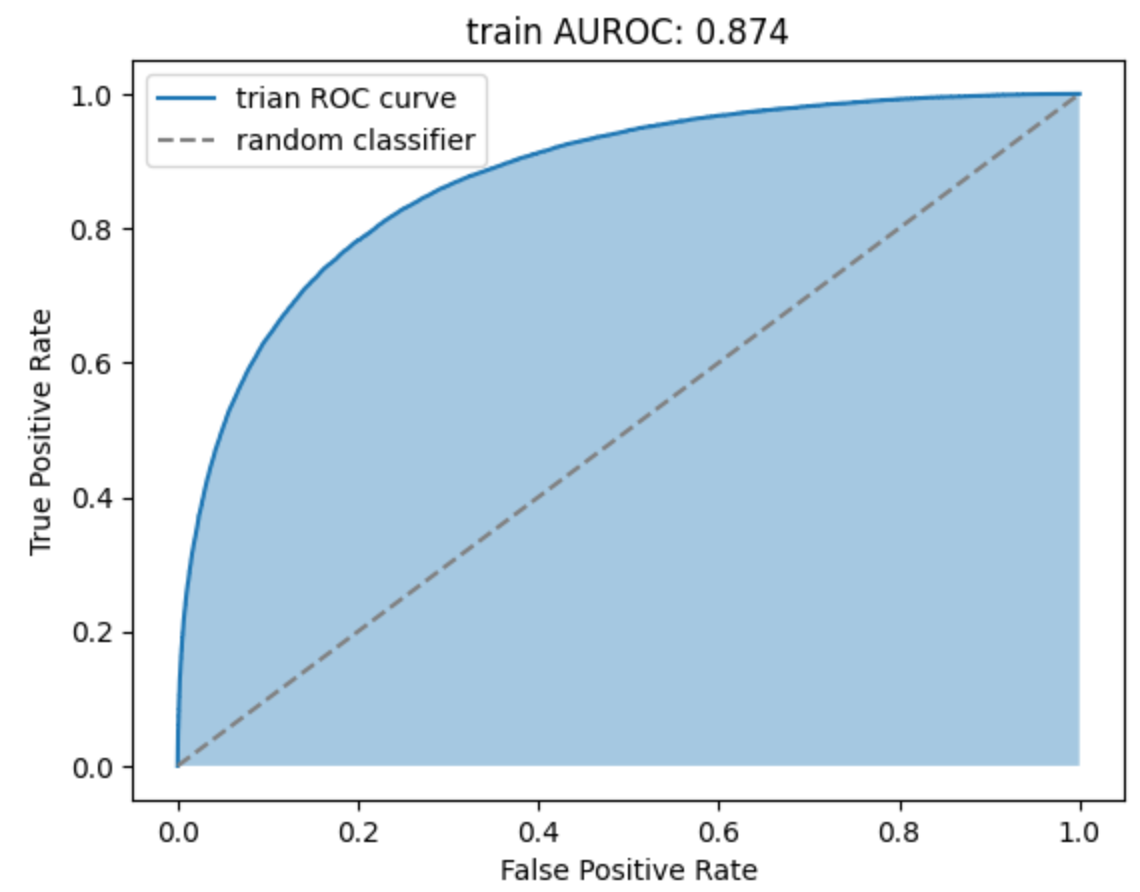
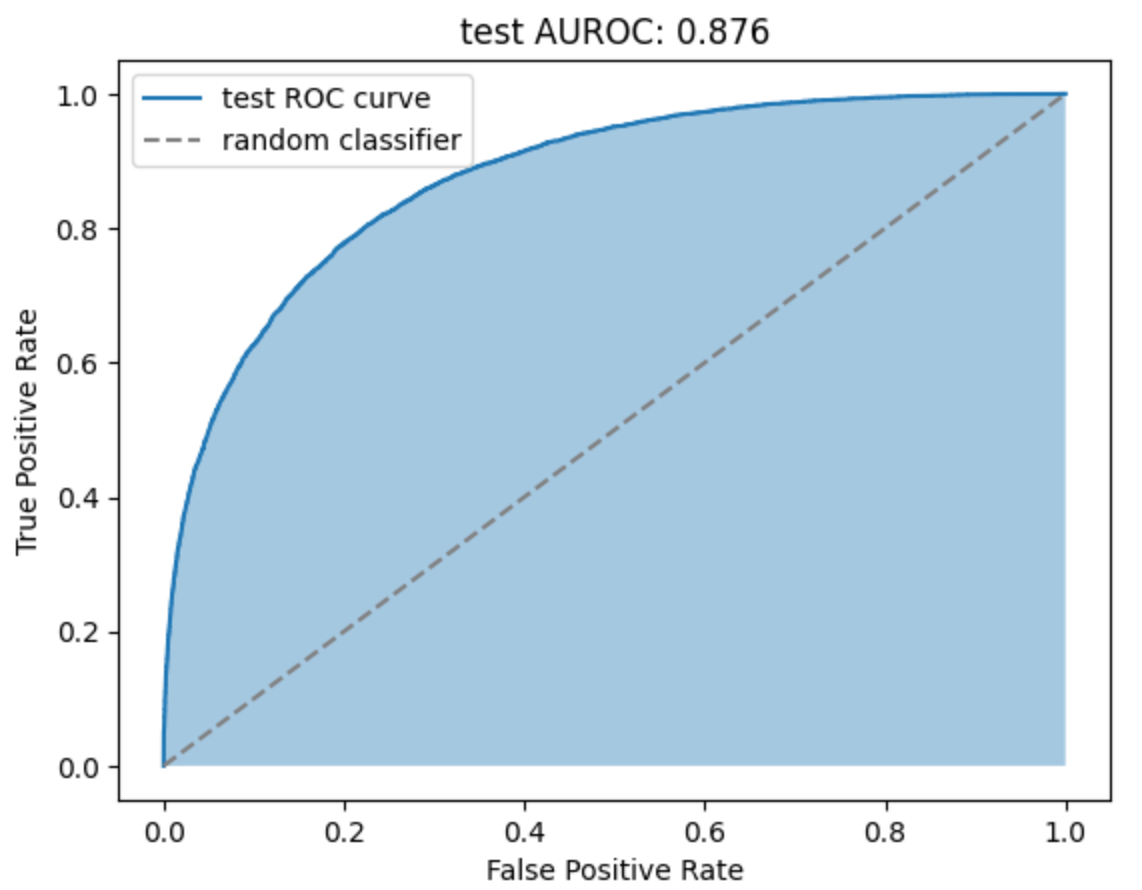
• ROC curve를 그렸을때 대각선에서 볼록하게 위로 멀어질수록 성능이 좋은 모델이라고 할 수 있다.
  이때 train, test의 ROC curve 모두 위쪽으로 볼록한 모양이므로 성능이 좋은 모델이라고 볼 수 있다.

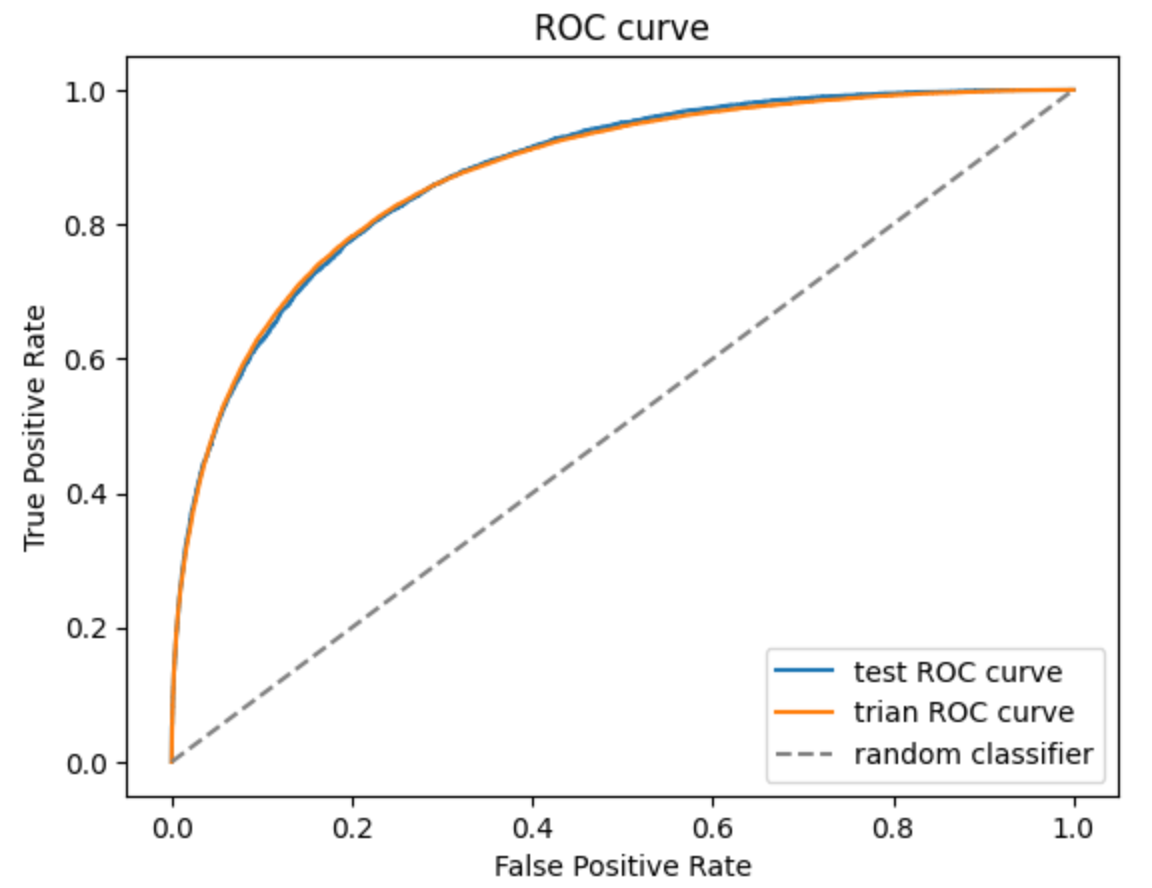
• AUROC는 ROC curve의 아래 면적을 계산한 값으로 1에 가까울수록 성능이 좋은 모델이다.
  trian, test 모두 약 0.87로 성능이 좋은 모델이다.

💡 한계점

• 현재의 데이터셋은 비가 오지 않은 날이 더 많기 때문에 클래스가 고르게 분포해있지 않고 정확도는 상대적으로 높지만 F1-score은 상대적으로 낮다.
  따라서 다수 클래스인 '비가 오지 않는 날'은 정확하게 예측하지만 소수 클래스인 '비오는 날'을 처리하는데 어려움이 있을 수 있다.
  threshold를 조정해보았지만 크게 개선하지 못했다. 오버샘플링이나 다른 학습 모델로 다시 시도해보는 것이 좋을 것 같다.

• 날씨는 날짜에 따라 데이터가 영향을 받는다고 생각하기 때문에 시계열 분석을 해본다면 예측 정확도가 더 높지 않았을까 하는 궁금증이 생겼다.
  다음에는 시게열 분석도 진행해보고 로지스틱 회귀 분석 결과와 비교해보면 좋을 것 같다.