Clustering in Python with Toy example
Clustering : Introduction
Clustering is
- data segmentation
- grouping
such that those within each cluster are more closely related to one another than objects in others. Note that clustering
- is , which means there is no right answer to learn
- the definition of (or , in the same meaning) is important (and subjective)
In this post, we will explore the followings:
- Generate a toy dataset for clustering
- Do cluster anlaysis on the dataset and visuakuzed this:
- K-means
- Gaussian mixture
- Hierachical clustering
- Self-Organizing Map
- Spectral clustering
- Evaluate clustering results
Settings in python
Libraries
Bring your packages to do cluster analysis and make plots in python:
import pandas as pd
import numpy as np
import math
import scipy as sp
import matplotlib.pyplot as pltExample data generation
To make a toy example data set, make_blobs in sklearn.datasets is used
make_blobsgenerate blobs for clustering- which means whose covariance is simplified as
- you can change the argument
random_stateand choose an appropriate- my choice is 7
- For more detailed information, visit here
from sklearn.datasets import make_blobs
x, y = make_blobs(n_samples=100, centers=3, n_features=2, random_state=7)
points = pd.DataFrame(x, y).reset_index(drop=True)
points.columns = ["x", "y"]
points.head()Check your generated toy using plot below: It is so pretty!
- As you may have already noticed, the number of clusters is 3
import seaborn as sns
sns.scatterplot(x="x", y="y", data=points, palette="Set2");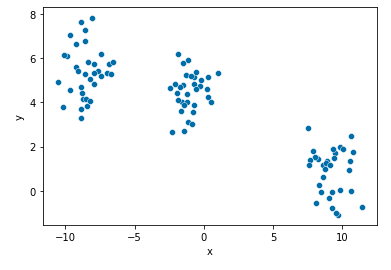
Color map
For a pretty visualization, I'd like to have three color palettes in advance:
import matplotlib.pyplot as plt
def get_cmap(n, name='viridis'):
'''Returns a function that maps each index in 0, 1, ..., n-1 to a distinct
RGB color; the keyword argument name must be a standard mpl colormap name.'''
return plt.cm.get_cmap(name, n)
cmap = get_cmap(3)Clustering algorithms
1. K-means
The - clustering is
- the most popular iterative descent clustering methods
- : identify a small subset that is likley to contain the optimal one, or at least a good suboptimal partition
A practical issue of K-means clustering on initial values:
- should start the algorithm with many different random choices for the starting means
- and choose the solution having smallest value of the objective function
- Fitting model
from sklearn.cluster import KMeans
model = KMeans(n_clusters = 3, random_state = 10)
model.fit(points)
kmeans_labels = model.fit_predict(points)
points['cluster'] = kmeans_labels- Plotting
import matplotlib.pyplot as plt
fig = plt.figure()
for i in range(len(points)):
plt.plot([points['x'][i]], [points['y'][i]], marker='o', color=cmap(points['cluster'][i]))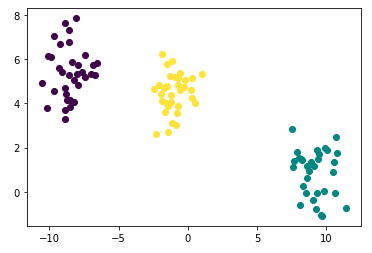
2. Gaussian mixture
The - clustering procedure is closely related to the algorithm for estimating a certain Gaussian mixture model
- K-means : deterministic
- Gaussian mixture : probabilistic
- They use concept the , using normal distribution centered on each centroid
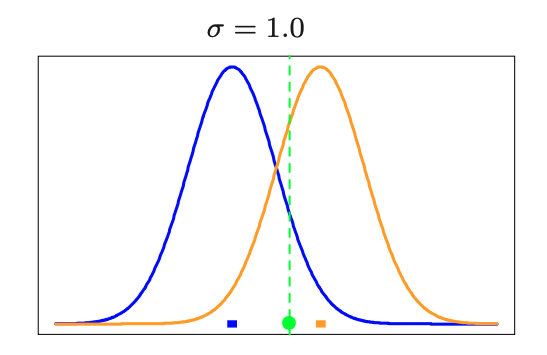
- They use concept the , using normal distribution centered on each centroid
For more on clustering using Gaussian mixture, go to here.
- Fitting model
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=3, random_state=42)
gmm_labels = gmm.fit_predict(points)
points['cluster'] = gmm_labels- Plotting
import matplotlib.pyplot as plt
fig = plt.figure()
for i in range(len(points)):
plt.plot([points['x'][i]], [points['y'][i]], marker='o', color=cmap(points['cluster'][i]))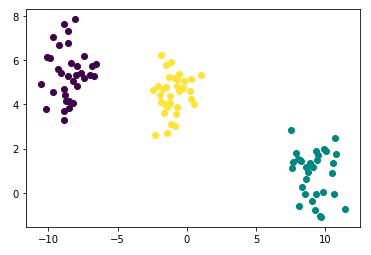
3. Hierachical clustering
- clustering algorithm depends on
- the choice for the number of clusters
- a (random) starting configuration assignment
In contrast, methods do not require such specifications. Instead, they require
- a measure of dissimilarity between disjoint of obsevations
Strategies for hierachical clustering divide into two basic paradigms:
- agglomerative (bottom-up) - mostly used
- divise (top-down)
For more detailed description, you can see this.
- Dendrogram
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 6))
plt.title("Customer Dendograms")
dend = shc.dendrogram(shc.linkage(points, method='ward'))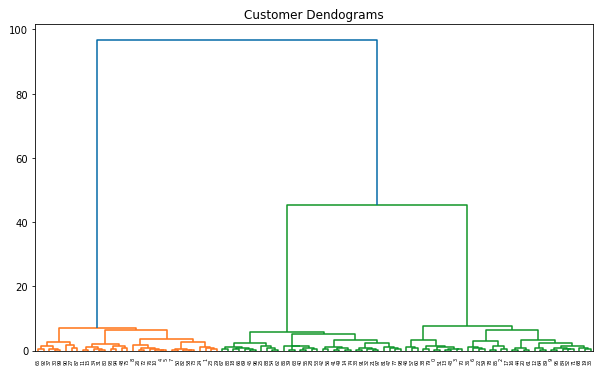
- Fitting model
from sklearn.cluster import AgglomerativeClustering
hierachical_fit = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='ward')
hac_labels = hierachical_fit.fit_predict(points)
points['cluster'] = hac_labels- Plotting
import matplotlib.pyplot as plt
fig = plt.figure()
for i in range(len(points)):
plt.plot([points['x'][i]], [points['y'][i]], marker='o', color=cmap(points['cluster'][i]))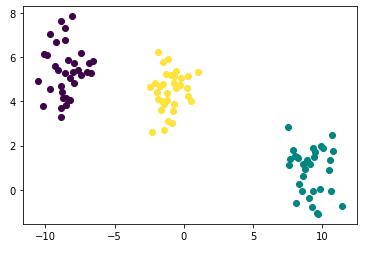
4. Self-Organizing Maps

The Self-Organizing Maps(SOM) procedure
- can be viewed as a constrained version of -
- tries to bend the plane so that the buttons(green dots) approximate the data points as well as possible
The original SOM algorithm was
- i.e., observations are processed one at a time
- Later, a batch version was proposed
Begin in Python! Package minisom do this.
- Data processing
- Note that function
MiniSomrequires data in array form, not in dataframe
- Note that function
points_dataset = []
for i in range(points.shape[0]):
point_series = np.array(points.iloc[i,:])
points_dataset.append(point_series)- Fitting model
from minisom import MiniSom
som = MiniSom(3, 1, # initialization of 3x3 SOM
len(points_dataset[0]), # length of dataset
sigma=0.3,
learning_rate = 0.1)
som.random_weights_init(points_dataset)
som.train(points_dataset, 1000)
win_map = som.win_map(points_dataset)- Plotting
import matplotlib.pyplot as plt
fig = plt.figure()
for i, (x, y) in enumerate(points_dataset):
fitted_ = som.winner(points_dataset[i])
cluster_number = (fitted_[0] * 1) + fitted_[1]
plt.plot([x], [y], marker='o', color=cmap(cluster_number))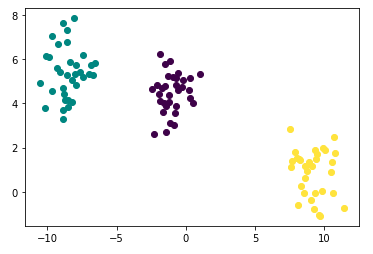
5. Spectral clustering
Traditional clustering method like K-means
- use a spherical or elliptical metric to group data points
- they will not work well for the other shape of clusters
is designed for
- the non-convex shape clusters, such as the concentric circles as below
- For detailed illustration, visit are here!
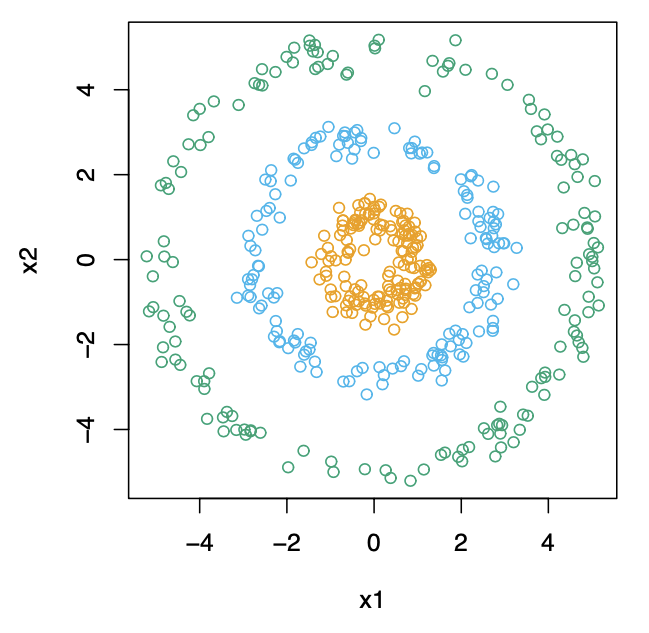
- Fitting model
from sklearn.cluster import SpectralClustering
sc = SpectralClustering(n_clusters=3).fit(points)
sc_labels = sc.labels_
points['cluster'] = sc_labels- Plotting
import matplotlib.pyplot as plt
fig = plt.figure()
for i in range(len(points)):
plt.plot([points['x'][i]], [points['y'][i]], marker='o', color=cmap(points['cluster'][i]))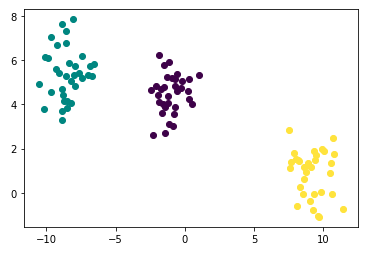
Performance evaluation
Clustering is the most representative
- means that the algorithm has no right answer to learn
- and also evaluating the algorithm is not a simple matter
For clustering, there are two types of evaluation criteria
- depending on whether they have a cluster label that is the correct answer or not
- Here, we assume that there is NO absolute right label for data
- For more description on clustering performace evaluation in python, go to here
Before compute out evaluation scores, we import metric from sklearn
from sklearn import metricsAlso, our dataset points is a pd.DataFrame like below
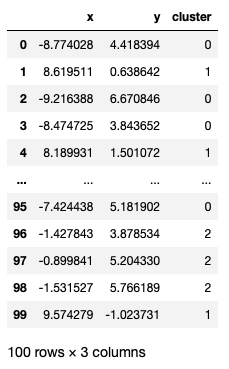
from sklearn import metrics
metrics.silhouette_score(points[["x", "y"]], np.ravel(points[["cluster"]]))from sklearn import metrics
metrics.silhouette_score(points[["x", "y"]], np.ravel(points[["cluster"]]))from sklearn import metrics
metrics.silhouette_score(points[["x", "y"]], np.ravel(points[["cluster"]]))[References]
- Hastie, T., Tibshirani, R., Friedman, J. (2008) The Elements of Statistical Learning : Data Mining, Inference, and Prediction. Springer
- https://towardsdatascience.com/time-series-clustering-deriving-trends-and-archetypes-from-sequential-data-bb87783312b4
- https://scikit-learn.org/stable/modules/clustering.html#clustering-performance-evaluation
