Porto Seguro’s Safe Driver Prediction

Kaggle Link : https://www.kaggle.com/code/yoontaeklee/porto-seguro-s-safe-driver-prediction

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.impute import SimpleImputer	# 결측치 대체
from sklearn.preprocessing import PolynomialFeatures	# 교호작용 변수 생성
from sklearn.preprocessing import StandardScaler

from sklearn.feature_selection import VarianceThreshold
# FeatureSelection에서 분산이 기준치보다 낮은 feature 탈락
from sklearn.feature_selection import SelectFromModel
# Feature Importance를 제공하는 모델의 importance를 활용하여 변수 선택

from sklearn,utils import shuffle
from sklearn,ensemble import RandomForestClassifier

pd.set_option('display.max_columns',100)

df_train = pd.read_csv("../input/porto-seguros-safe-driver-prediction-dataset/train.csv")
df_test = pd.read_csv("../input/porto-seguros-safe-driver-prediction-dataset/test.csv")

1. 데이터셋 확인

df_train.head()

df_train.tail()

df_train.shape

# (595212, 59)

1.1 Null data 확인

• Null data 개수 확인

df_train.isnull().sum()

• 실제 기업 데이터이기 때문에 feature들을 비식별화 해놓음
• isnull() 사용 불가 -> -1인 값 찾아야함
• feature들이 grouping 되어있음
• 타겟값은 이전 보험 청구 여부에 따라 0 혹은 1

1.2 Metadata

• 데이터 역할 : ID, target, input
• 데이터 레벨 : nominal, interval, ordinal, binary
• 필요 / 불필요 : True / False
• 데이터 타입 : int, float, str

data = []

for f in df_train.columns:
	# 데이터 역할 지정
    if f == 'target':
    	role = 'target';
    elif f == 'id':
    	role = 'id'
    else:
    	role = 'input'
    
    # 데이터 레벨 지정
    if 'bin' in f or f == 'target':
    	level = 'binary'
    elif 'cat' in f or f == 'id':
    	level = 'nominal'
    elif df_train[f].dtype == float:
    	level = 'interval'
    elif df_train[f].dtype == int:
    	level = 'ordinal'
        
    # id는 False 지정
    keep = True
    if f == 'id':
    	keep = False
        
    # 데이터 타입 지정
    dtype = df_train[f].dtype
    
    # DataFrame으로 만들기 위해 딕셔너리 타입으로 생성
    f_dict = {
    	'varname': f,
        'role': role,
        'level': level,
        'keep': keep,
        'dtype': dtype
    }
    data.append(f_dict)

meta = pd.DataFrame(data, columns = ['varname','role','level','keep','dtype'])
meta.set_index('varname',inplage = True)

2. 탐색적 데이터 분석(Exploratory Data Analysis)

• 시각화 라이브러리는 matplotlib, seaborn, plotly 등 목적에 맞게 사용하여 참고

2.1 Interval 변수

Interval = meta[(meta['level'] == 'interval') & (meta['keep'])].index

# describe 사용하여 interval 변수 통계량 확인
df_train[Interval].describe()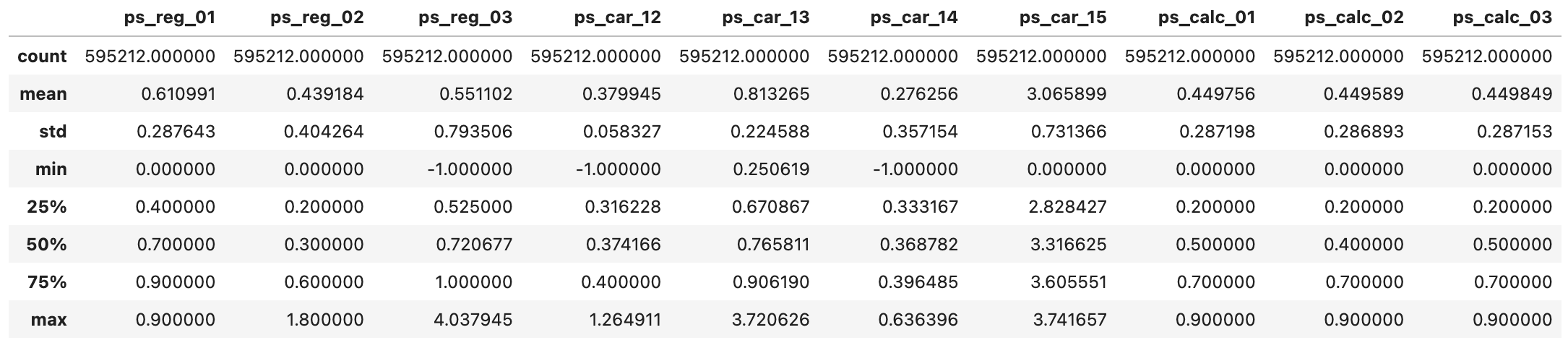

1) 결측치 확인

• 위에 언급하였듯 isnull()이 아닌 -1 값 확인
• ps_reg_03, ps_car_12, ps_car_14

2) 변수들 사이 범위 확인

• Scaling 여부 확인 (여기서는 트리모델 사용 -> 불필요)

3) 변수들 숫자 크기 확인

• 평균값으로 보나, max값으로 보나 변수의 크기가 크지 않음

2.2 Ordinal 변수

Ordinal = meta[(meta['level'] == 'ordinal') & (meta['keep'])].index

df_train[Ordinal].describe()

1) 결측치 확인

• ps_car_11
  외엔 Interval 변수와 크게 다르지 않음

2.3 Binary 변수

Binary = meta[(meta['level'] == 'binary') & (meta['keep'])].index

df_train[Binary].describe()

1) 결측치 확인

• 결측치 X

2) 변수들 사이의 범위 확인

• Binary 데이터이기 때문에 범위 확인할 필요 X

3) Target 변수 확인

• Target 데이터가 해당 대회의 핵심
• 데이터는 0 or 1이기 때문에 균형이 맞기 위해선 평균이 0.5
• Target의 평균은 0.0364로, 0이 훨씬 많음
• Metric으로 Normalized Gini Coefficient를 사용하는 이유

--------불균형 데이터 어떻게 처리하는가--------

2.4 Imbalanced Class

• Target 값이 0인 것이 1인 것보다 훨씬 많음
• Imbalanced한 데이터는 일반적으로 Undersampling 혹은 Oversampling으로 처리
• Undersampling : 0이 1보다 훨씬 많으므로 0인 데이터를 줄여 균형을 맞춤
• Oversampling : 0이 1보다 훨씬 많으므로 1인 데이터를 늘려 균형을 맞춤
• 데이터셋의 크기를 기준으로 선택(데이터가 많으면 Undersampling)

f, ax = plt.subplots(figsize = (8,8))
df_train['target'].value_counts().plot.pie(explode = [0, 0.1],
	autopct = '%1.1f%%', shadow = True,
    colors = ['lightcoral','lightskyblue'], textprops={'fontsize':18})
plt.title('Target PiePlot', size = 20)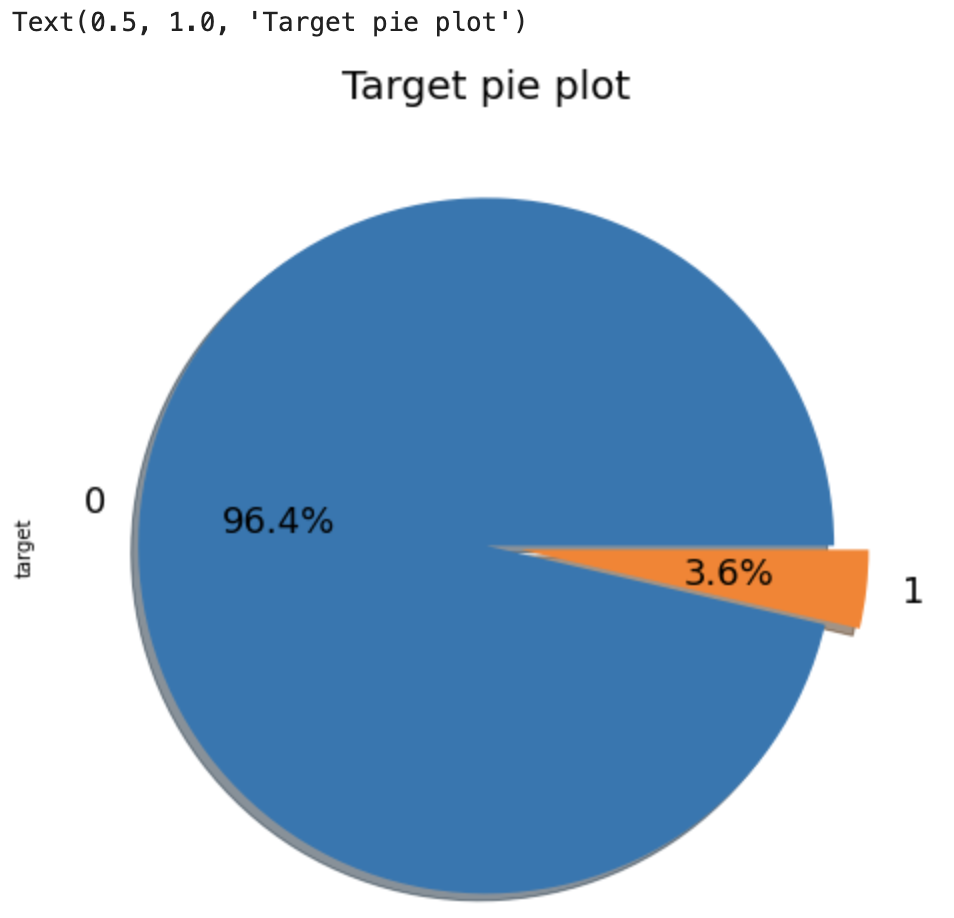

Undersampling code

# 언더샘플링 비율
desired_apriori=0.10

# target 변수의 클래스에 따른 인덱스 지정
idx_0 = df_train[df_train['target'] == 0].index
idx_1 = df_train[df_train['target'] == 1].index

# 지정해준 인덱스로 클래스 길이(레코드 수) 지정
nb_0 = len(df_train.loc[idx_0])
nb_1 = len(df_train.loc[idx_1])

# undersampling
undersampling_rate = ((1-desired_apriori)*nb_1)/(nb_0*desired_apriori)
undersampled_nb_0 = int(undersampling_rate*nb_0)
print('target = 0 에 대한 언더샘플링 비율 : {}'.format(undersampling_rate))
print('언더샘플링 전 target = 0 레코드 수 : {}'.format(nb_0))
print('언더샘플링 후 target = 0 레코드 수 : {}'.format(undersampled_nb_0))

# 언더샘플링 비율이 적용된 개수만큼 랜덤하게 샘플을 뽑아 인덱스 저장
undersampled_idx = shuffle(idx_0, random_state=37,
						n_samples=undersampled_nb_0)

# 언더샘플링 인덱스와 클래스 1의 인덱스를 리스트로 저장
idx_list = list(undersampled_idx) + list(idx_1)

# 저장한 인덱스로 train셋 인덱싱
df_train = df_train.loc[idx_list].reset_index(drop=True)

2.5 결측치 확인

• 결측치가 얼마나 있는지 확인

vars_with_missing = []

# 모든 컬럼에 -1이라는 값이 1개 이상 있는 것을 확인하여 출력
# 어느 변수에 몇개의 레코드가 있는지, 비율은 얼마나 되는지 확인하여 출력
for f in df_train.columns:
	missings = df_train[df_train[f] == -1][f].count()
    if missings > 0:
    	vars_with_missing.append(f)
        missings_perc = missings/df_train.shape[0]
        
        print('Variable {}\t has {:10} records\t ({:.2%})\t with missing 			values'.format(f, missings, missings_perc))
print()
print('There are {} variables with missing values total'.format(len(vars_with_missing)))

결측치 해석

• ps_car_03_cat, ps_car_05_cat은 결측치가 많기 때문에 변수 제거
• ps_reg_03의 경우 평균으로 대체
• ps_car_11의 경우 결측치가 1개 이므로 최빈값으로 대체(순서형 변수이므로)
• 결론적으로 연속형 변수는 mean, 범주형 변수는 mode로 채우기

# 결측치가 많은 변수 제거
vars_to_drop = ['ps_car_03_cat','ps_car_05_cat']
df_train.drop(vars_to_drop, inplace=True, axis=1)

# 만들어두었던 메타데이터 업데이터 (버린 변수 keep=True -> False)
meta.loc[(vars_to_drop),'keep'] = False

# 그 외 결측치는 평균 혹은 최빈값으로 대체
# SimpleInputer 사용
mean_imp = SimpleImputer(missing_values=-1, strategy='mean')
mode_imp = SimpleImputer(missing_values=-1, strategy='most_frequent')
df_train['ps_reg_03'] = mean_imp.fit_transform(df_train[['ps_reg_03']])
df_train['ps_car_12'] = mean_imp.fit_transform(df_train[['ps_car_12']])
df_train['ps_car_14'] = mean_imp.fit_transform(df_train[['ps_car_14']])
df_train['ps_car_11'] = mode_imp.fit_transform(df_train[['ps_car_11']])

2.6 범주형 변수의 unique값 확인

• 범주형 변수가 모두 숫자로 매핑되어 있음
• 범주형 변수의 유니크 값과 몇 개의 유니크 값이 있는지 확인

Nominal = meta[(meta['level'] == 'nominal') & (meta['keep'])].index

for f in Nominal:
	dist_values = df_train[f].value_counts().shape[0]
    print('Variable {} has {} distinct values'.format(f, dist_values))

2.7 범주형 변수 인코딩

• 범주형 변수는 일반적으로 one-hot-encoding, Label-encoding 방법 사용
• one-hot-encoding은 변수에 높고 낮음이 부여되지 않기 때문에 target을 예측하는데에 영향을 주지 않지만 unique값이 많을 경우 sparse한 벡터가 생성되고 feature 또한 급격하게 늘어나기 때문애 cost가 늘어나고 차원의 저주에 빠질 확률이 높아짐
• Label-encoding은 feature가 유지되기 때문에 cost가 적고 차원을 신경쓸 필요가 없지만 각 unique 값에 매핑되는 숫자에 순서가 생기기 때문에 target 예측에 영향을 줄 수 있음

mean-encoding

• 캐글에서는 mean-encoding, frequency-encoding 을 많이 사용
• 차원의 저주에 빠질 일이 없고 빠르다는 장점이 있음
• 가장 큰 장점으로는 target과의 평균을 취해주었기 때문에 상관관계를 가짐
• BUT Data Leakage문제와 오버피팅 문제 생길 수 있음
• test 및 추후 수집될 데이터 셋에 대한 target 값을 알지 못하기 때문에 target에 대한 평균을 train 데이터 셋으로만 적용시켜야함
• 때문에 test 셋의 target값을 사용하게 되면 data leakage 문제가, train 셋의 target 값만 사용하게 되면 오버피팅 되는 딜레마가 생김
• 해당 커널에서는 오버피팅 방지를 위해 noise를 추가하고, smoothing을 적용함
• smoothing을 통해 평균값이 치우친 상황을 보완해줄 수 있음

# 오버피팅 방지를 위한 noise 추가
# smoothing을 통해 치우쳐진 평균값 보정

def add_noise(series, noise_level):
    return series * (1 + noise_level * np.random.randn(len(series)))

def target_encode(trn_series=None, tst_series=None, target=None, min_samples_leaf=1, smoothing=1, noise_level=0):
    assert len(trn_series) == len(target)
    assert trn_series.name == tst_series.name
    temp = pd.concat([trn_series, target], axis=1)
    averages = temp.groupby(by=trn_series.name)[target.name].agg(['mean','count'])
    # 오버피팅 방지를 위한 smoothing
    smoothing = 1 / (1 + np.exp(-(averages['count'] - min_samples_leaf) / smoothing))
    prior = target.mean()
    averages[target.name] = prior * (1 - smoothing) + averages['mean'] * smoothing
    averages.drop(['mean','count'], axis=1, inplace=True)
    ft_trn_series = pd.merge(trn_series.to_frame(trn_series.name), averages.reset_index().rename(columns={'index': target.name, target.name: 'average'}),on=trn_series.name, how='left')['average'].rename(trn_series.name + '_mean').fillna(prior)
    ft_trn_series.index = trn_series.index
    ft_tst_series = pd.merge(tst_series.to_frame(tst_series.name),averages.reset_index().rename(columns={'index': target.name, target.name: 'average'}),on=tst_series.name, how='left')['average'].rename(trn_series.name + '_mean').fillna(prior)
                        
    ft_tst_series.index = tst_series.index
    return add_noise(ft_trn_series, noise_level),add_noise(ft_tst_series, noise_level)

# 위에서 구현한 함수를 ps_car_11_cat(104개의 유니크 값)에 적용
# feature가 바뀌었으므로 메타데이터 업데이트
train_encoded, test_encoded = target_encode(df_train['ps_car_11_cat'],df_test['ps_car_11_cat'],target=df_train.target,min_samples_leaf=100,smoothing=10,noise_level=0.01)
df_train['ps_car_11_cat_te'] = train_encoded
df_train.drop('ps_car_11_cat', axis=1, inplace=True)
meta.loc['ps_car_11_cat', 'keep'] = False
df_test['ps_car_11_cat_te'] = test_encoded
df_test.drop('ps_car_11_cat', axis=1, inplace=True)

2.8 시각화를 통한 EDA

1) 범주형 변수 시각화

Nominal = meta[(meta['level'] == 'nominal') & (meta['keep'])].index

# 변수별로 barplot
for f in Nominal:
	plt.figure()
    fig, ax = plt.subplots(figsize=(20,10))
    ax.grid(axis = 'y', linestyle = '--')
    
    cat_perc = df_train[[f, 'target']].groupby([f], as_index=False).mean()
    cat_perc.sort_values(by='target', ascending=False, inplace=True)
    
    # 위의 계산을 통해 나온 비율로 target=1의 데이터 중 어떤 유니크 값의 비율이 높은지 확인
    sns.barplot(ax=ax, x=f, y='target', palette='Pastel1', edgecolor='black', linewidth=0.8, data=cat_perc, order=cat_perc[f],)
    plt.ylabel('% target', fontsize=18)
    plt.xlabel(f, fontsize=18)
    plt.tick_params(axis='both', which='major', labelsize=18)
    plt.show()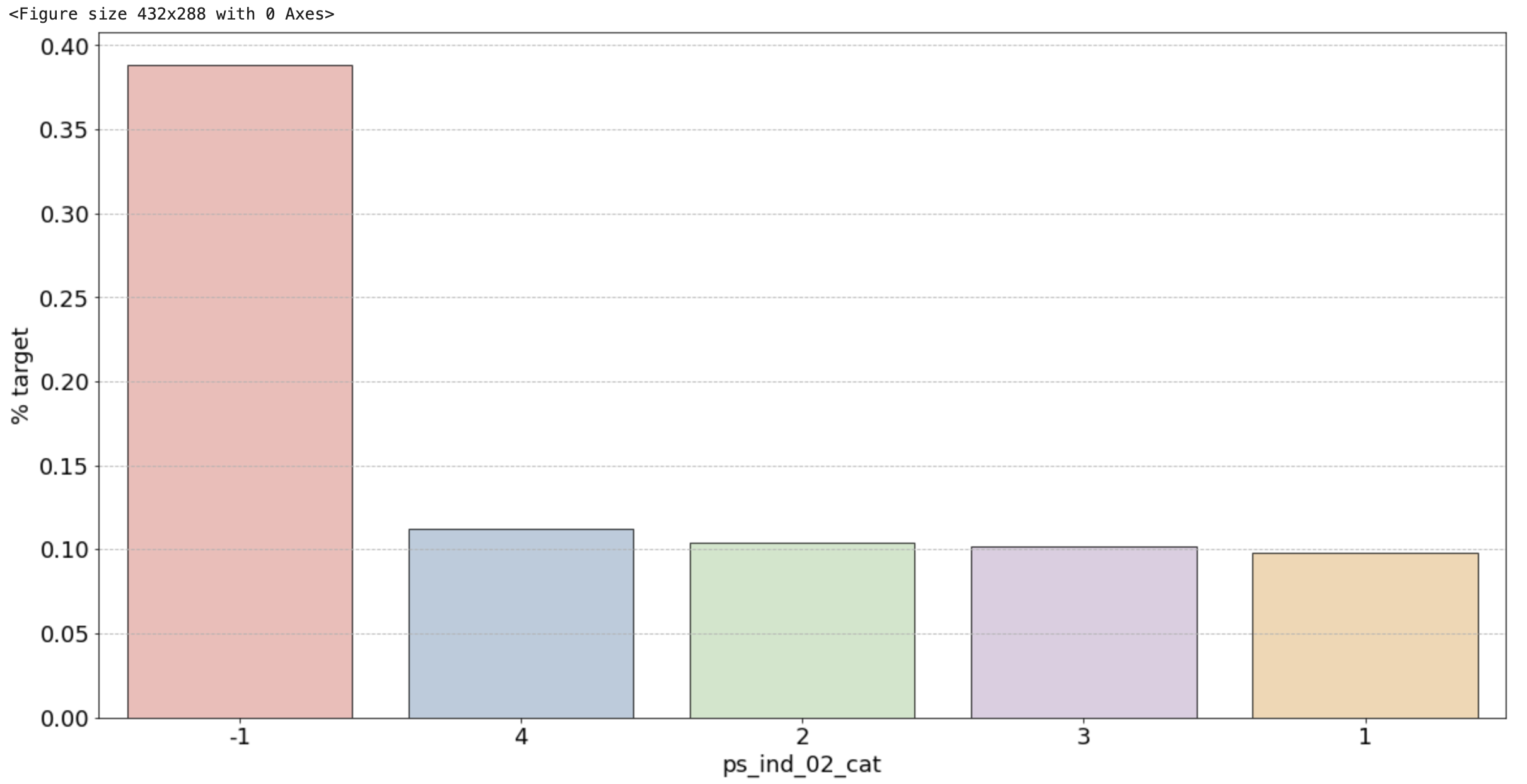

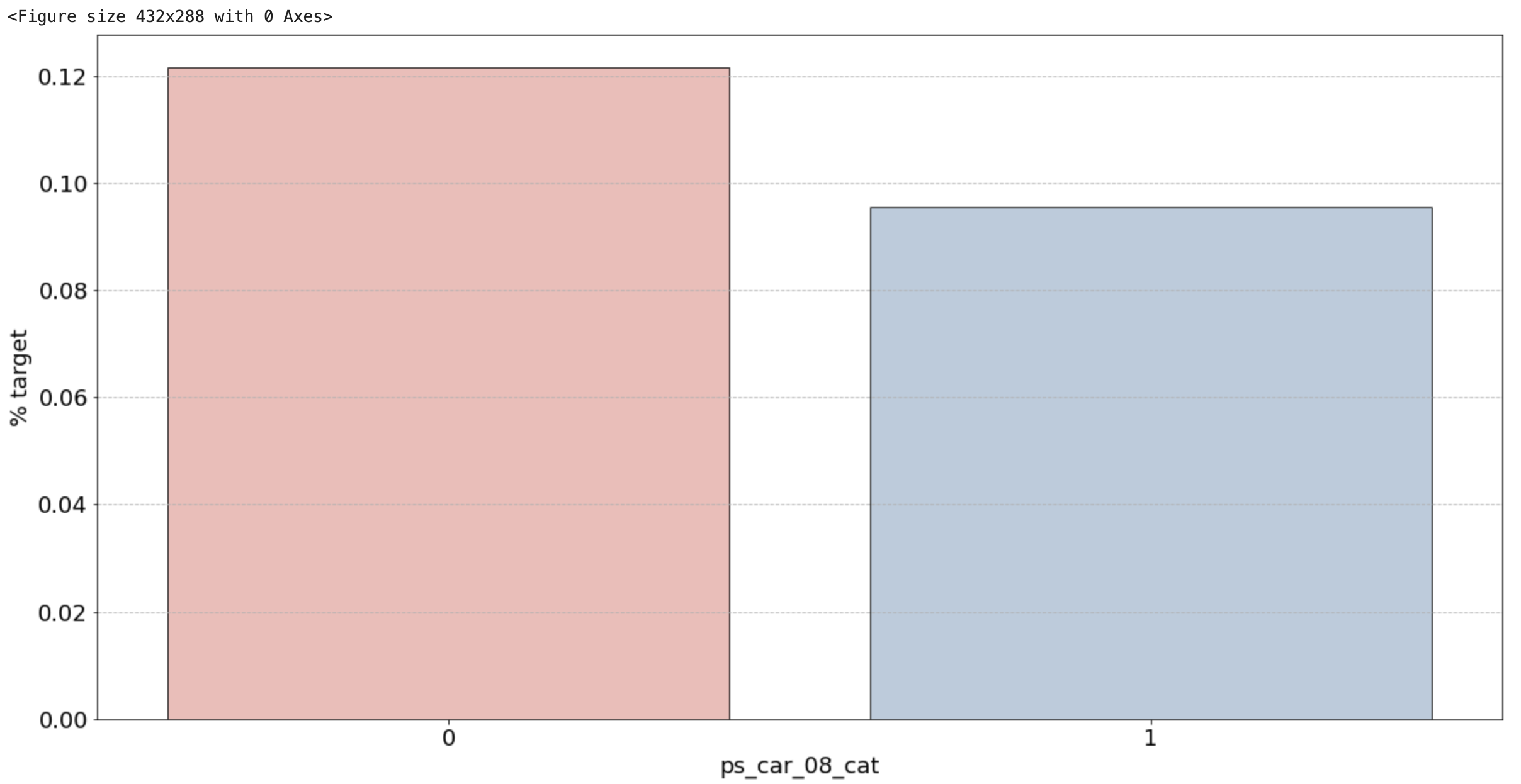
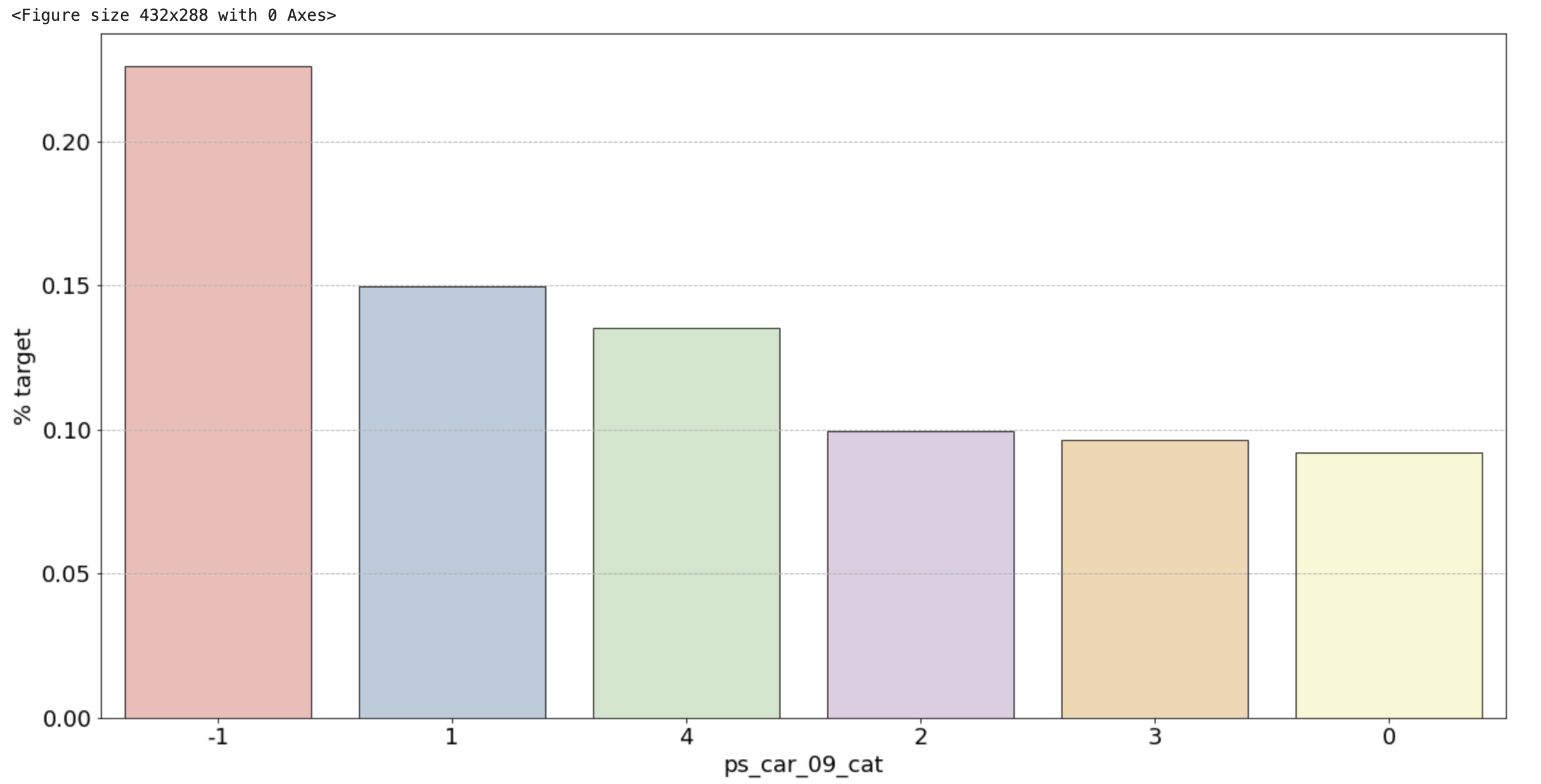
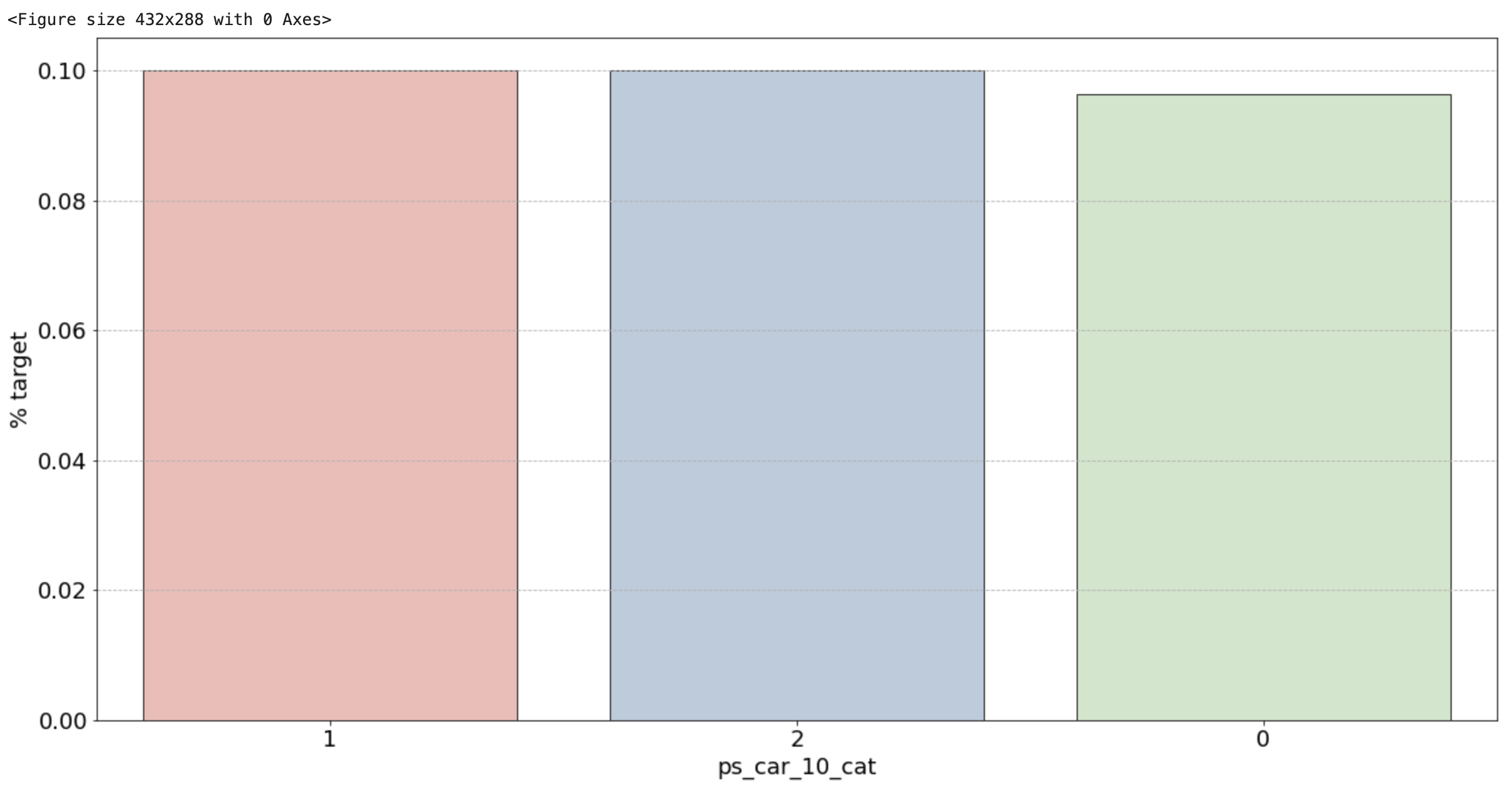
2) 범주형 변수 시각화 결과

• ps_ind_02_cat: -1(결측치)의 경우 target = 1의 데이터가 40%를 차지하고, 나머지는 10% 정도로 보임. target에 대한 비율이기 때문에 50%에 가까울수록 애매한 unique 값. 10%를 보이는 나머지 unique 값들이 보험 청구를 안할 확률이 높다는 뜻이므로 오히려 확실한 정보
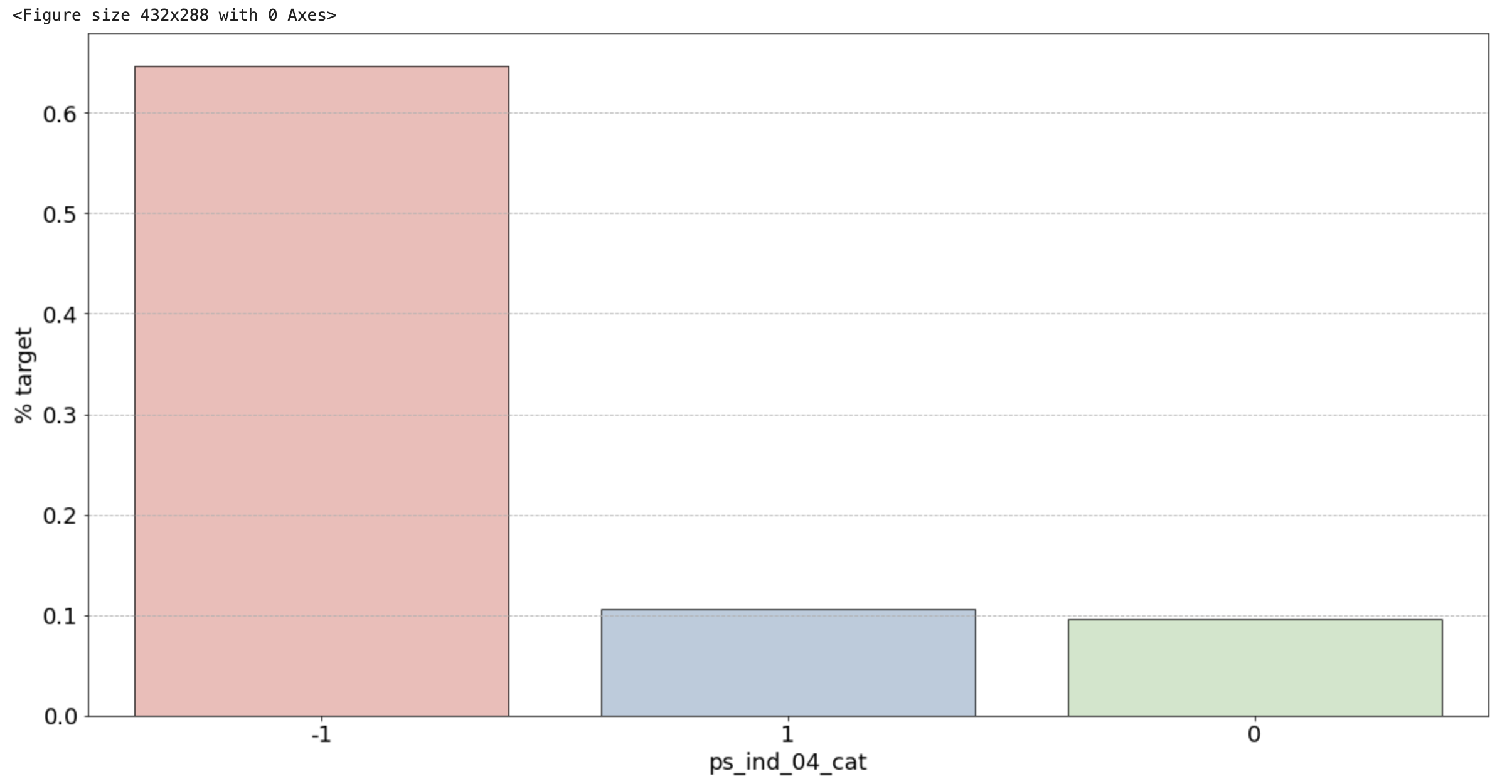
• ps_ind_04_cat: -1(결측치)가 65% 정도로 target = 1의 값을 가지므로 보험을 청구할 확률이 높음
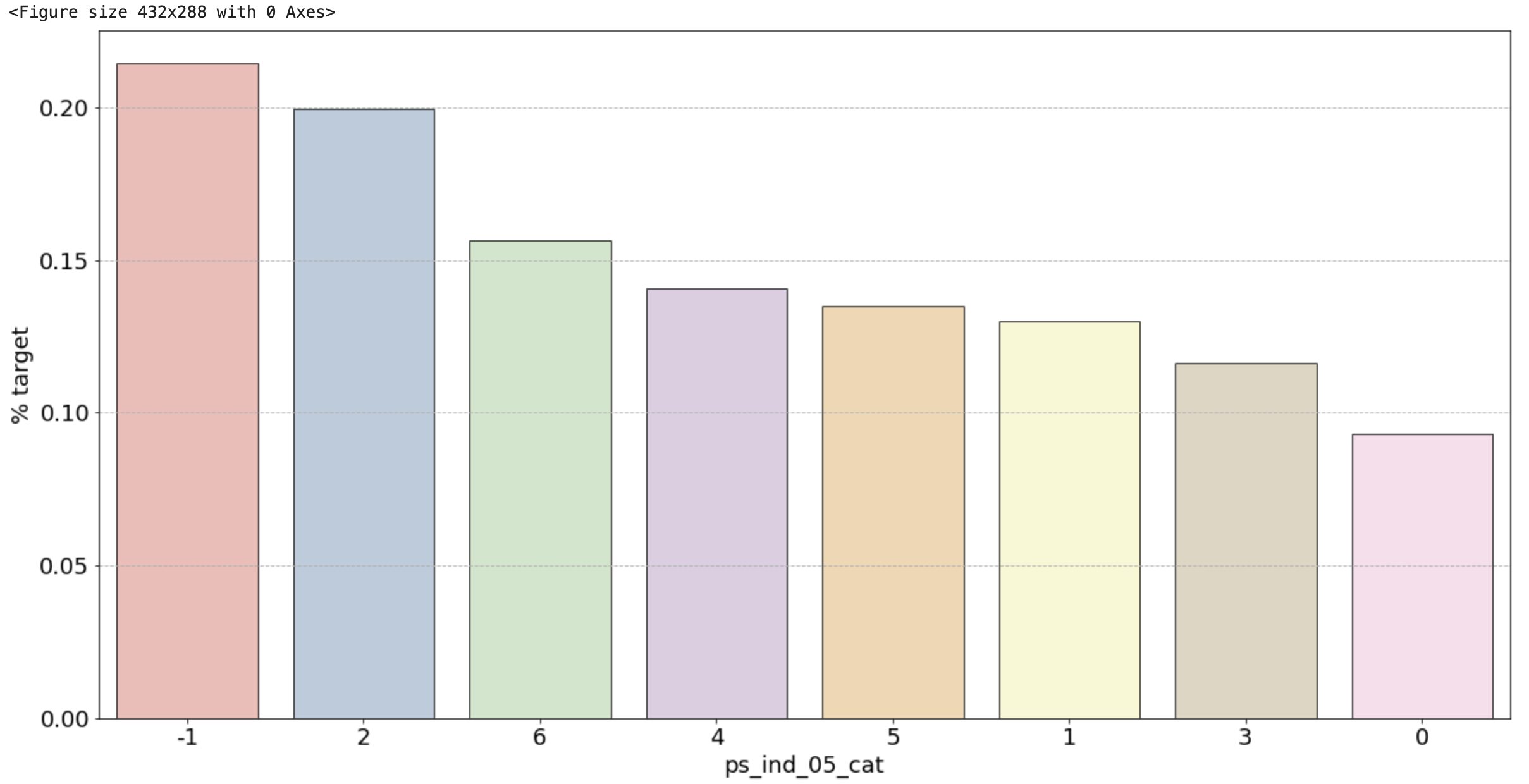
• ps_ind_05_cat: 눈에 띄는 unique 값은 없습니다.
• ps_car_01_cat: -1(결측치)가 거의 50%에 가까우므로 애매. 나머지 값은 다 보험을 청구하지 않을 확률이 높아보임
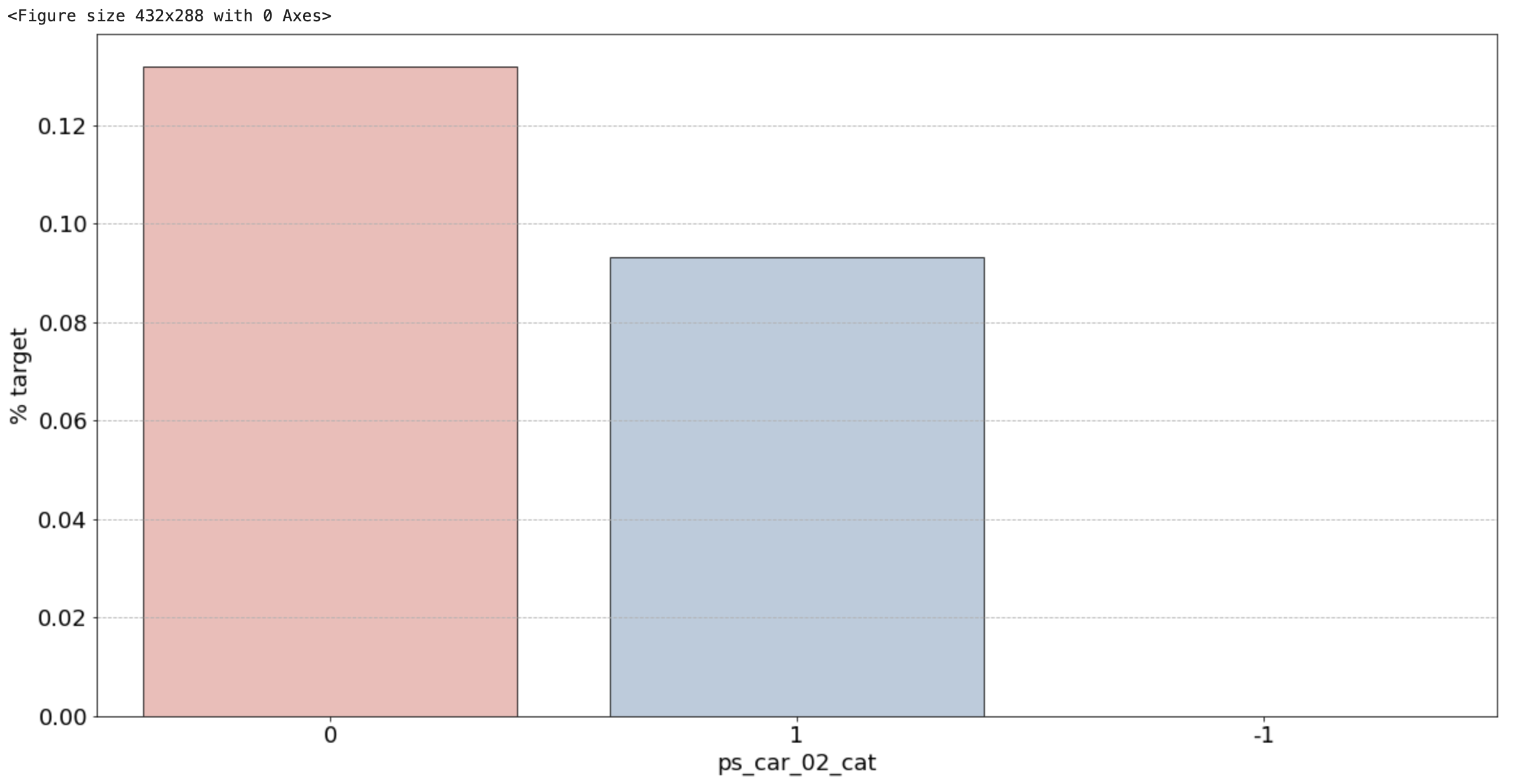
• ps_car_02_cat: -1(결측치)가 0%. 보험을 절대 청구하지 않을 것
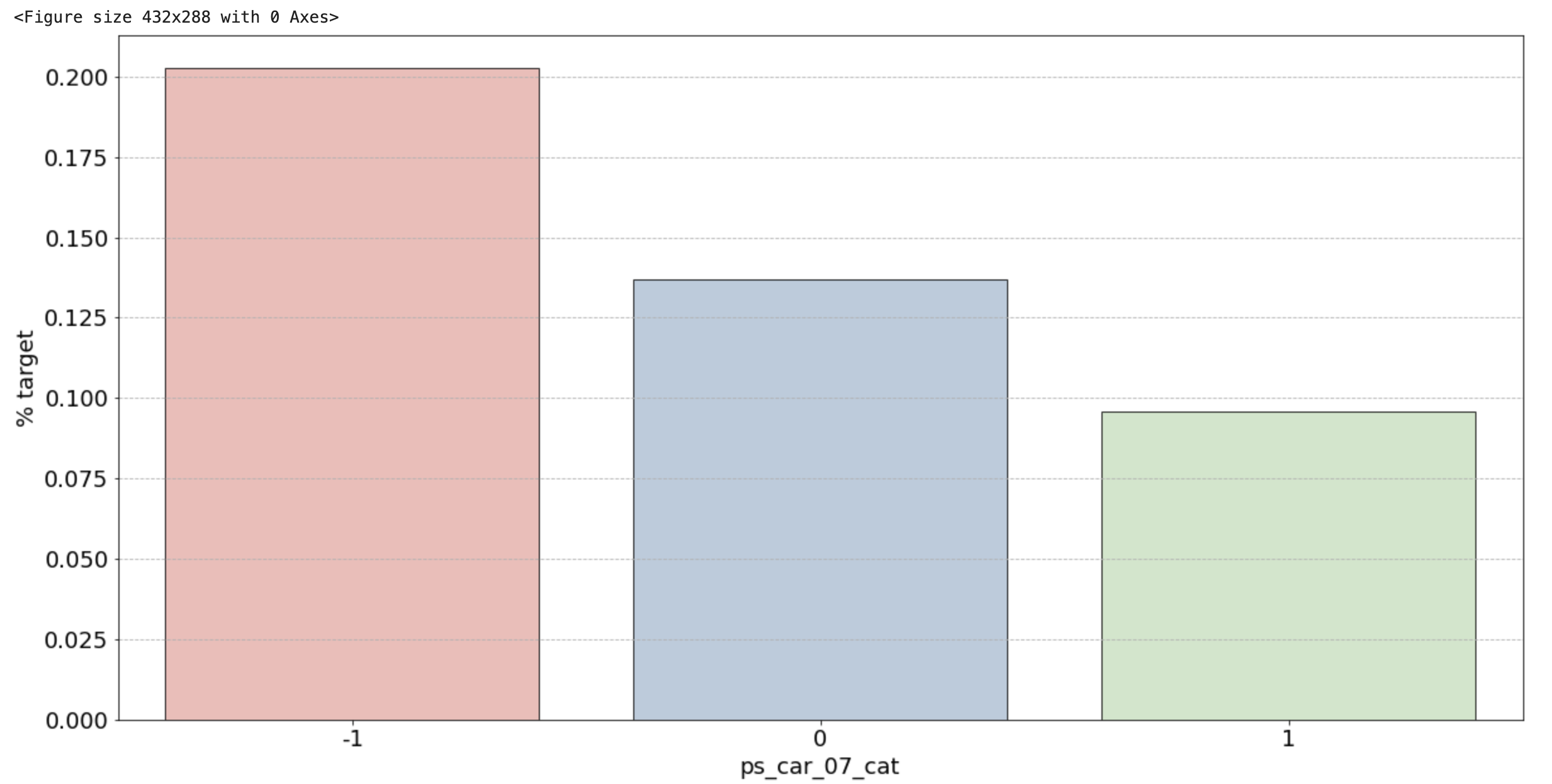
• 그 외: unique 값 마다 어느정도 차이들이 있음

3) Interval 변수 시각화(연속형)

def corr_heatmap(Interval):
    correlations = df_train[Interval].corr()

    # Create color map ranging between two colors
    cmap = sns.diverging_palette(220, 10, as_cmap=True)

    fig, ax = plt.subplots(figsize=(10,10))
    sns.heatmap(correlations, cmap=cmap, vmax=1.0, center=0, fmt='.2f',
                square=True, linewidths=.5, annot=True, cbar_kws={"shrink": .75})
    plt.show();
    
Interval = meta[(meta["role"] == "target") | (meta["level"] == 'interval') & (meta["keep"])].index
corr_heatmap(Interval)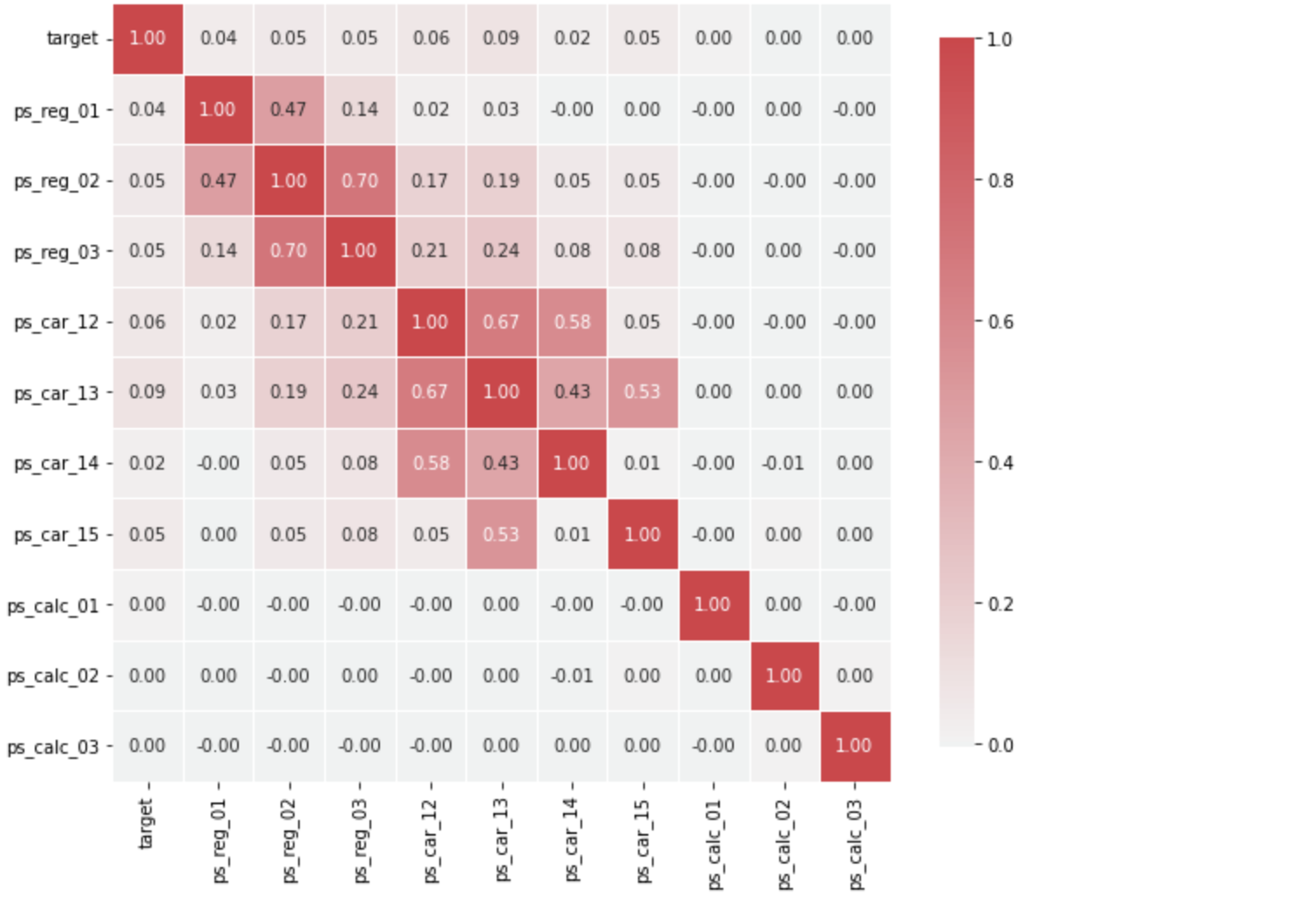

• 강한 상관관계를 가지는 변수들 시각화 필요

ps_reg_02 & ps_reg_03

sns.lmplot(x='ps_reg_02', y='ps_reg_03', data=df_train, hue='target', palette='Set1', scatter_kws={'alpha':0.3})
plt.show()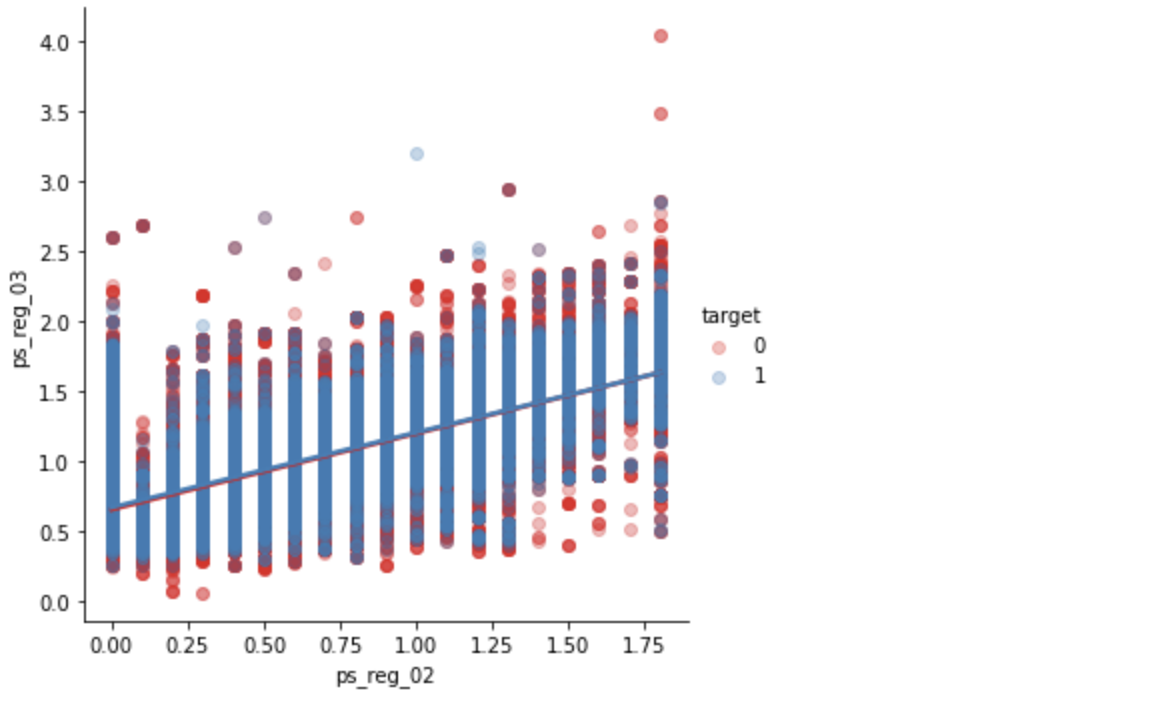

ps_car_12 & ps_car_13

sns.lmplot(x='ps_reg_02', y='ps_reg_03', data=df_train, hue='target', palette='Set1', scatter_kws={'alpha':0.3})
plt.show()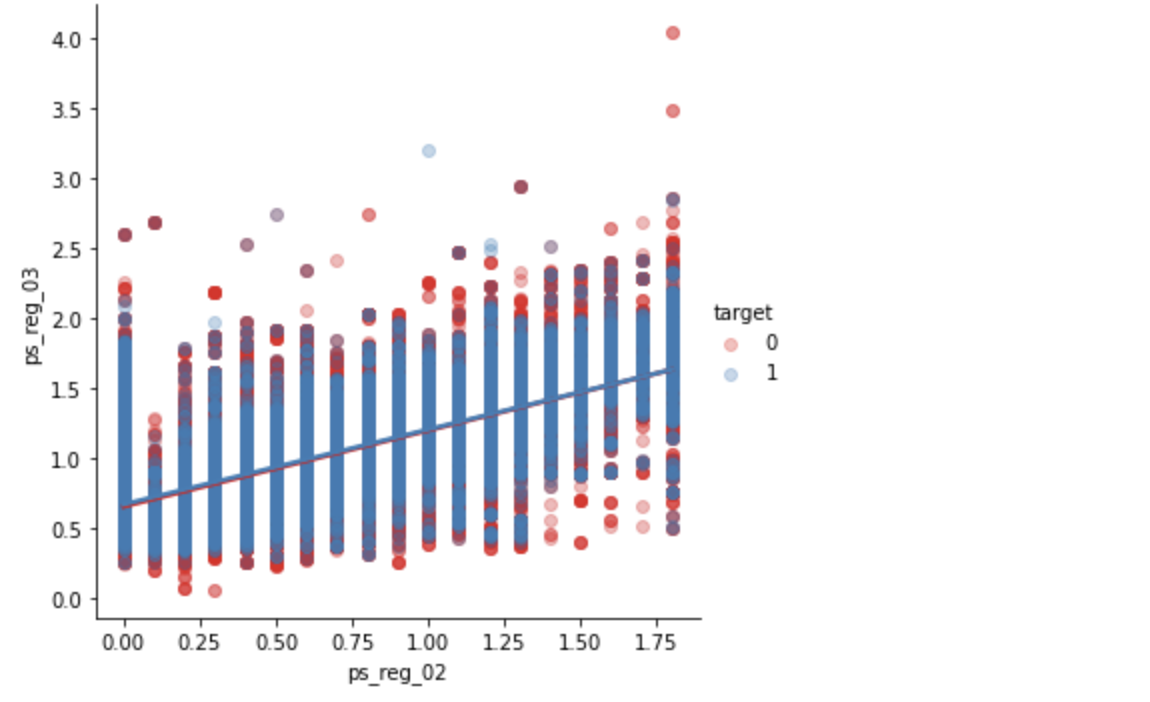

ps_car_12 and ps_car_14

sns.lmplot(x='ps_car_12', y='ps_car_14', data=df_train, hue='target', palette='Set1', scatter_kws={'alpha':0.3})
plt.show()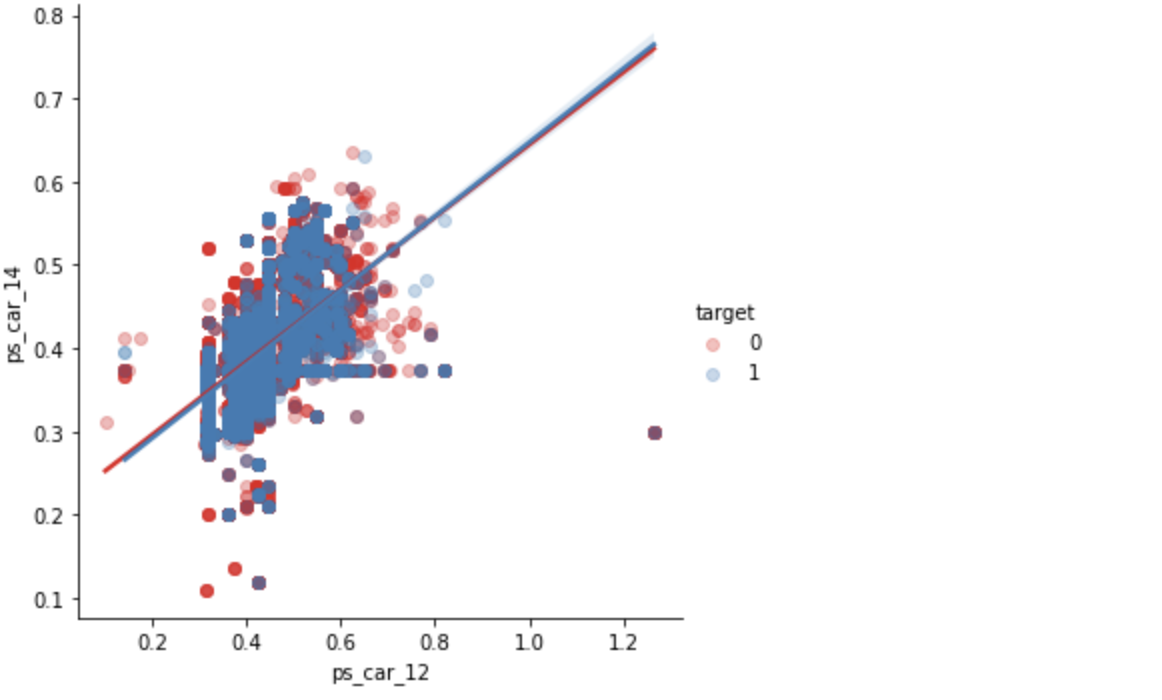

ps_car_13 & ps_car_15

sns.lmplot(x='ps_car_15', y='ps_car_13', data=df_train, hue='target', palette='Set1', scatter_kws={'alpha':0.3})
plt.show()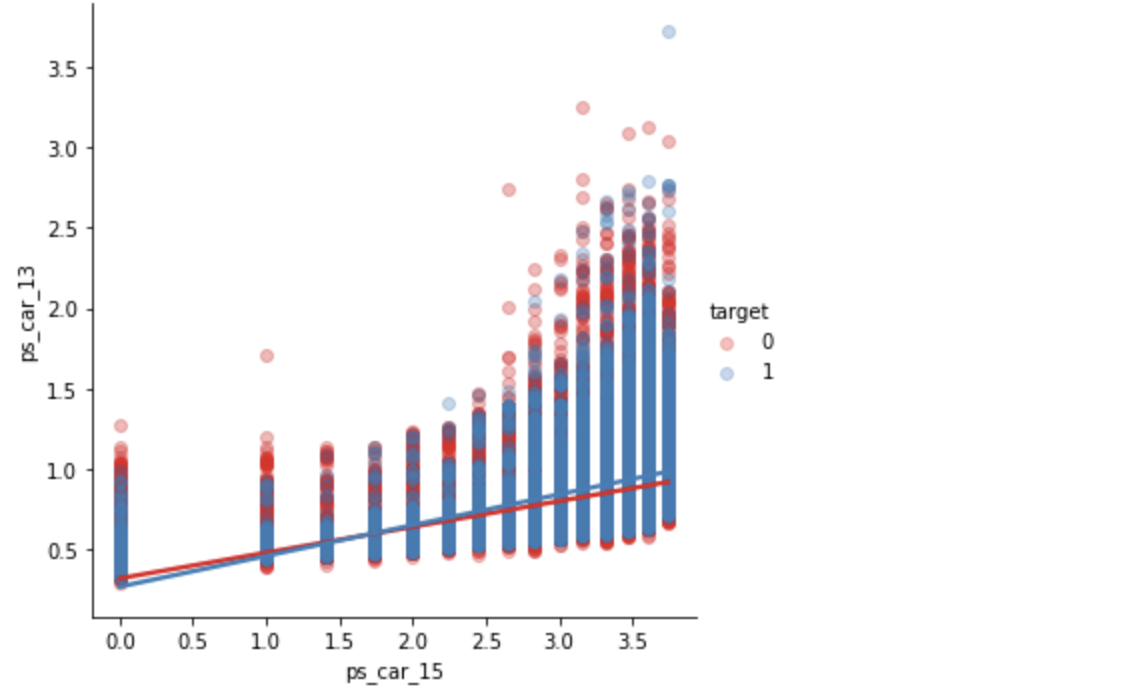

4) Ordinal 변수 시각화

Ordinal = meta[(meta["role"] == "target") | (meta["level"] == 'ordinal') & (meta["keep"])].index
corr_heatmap(Ordinal)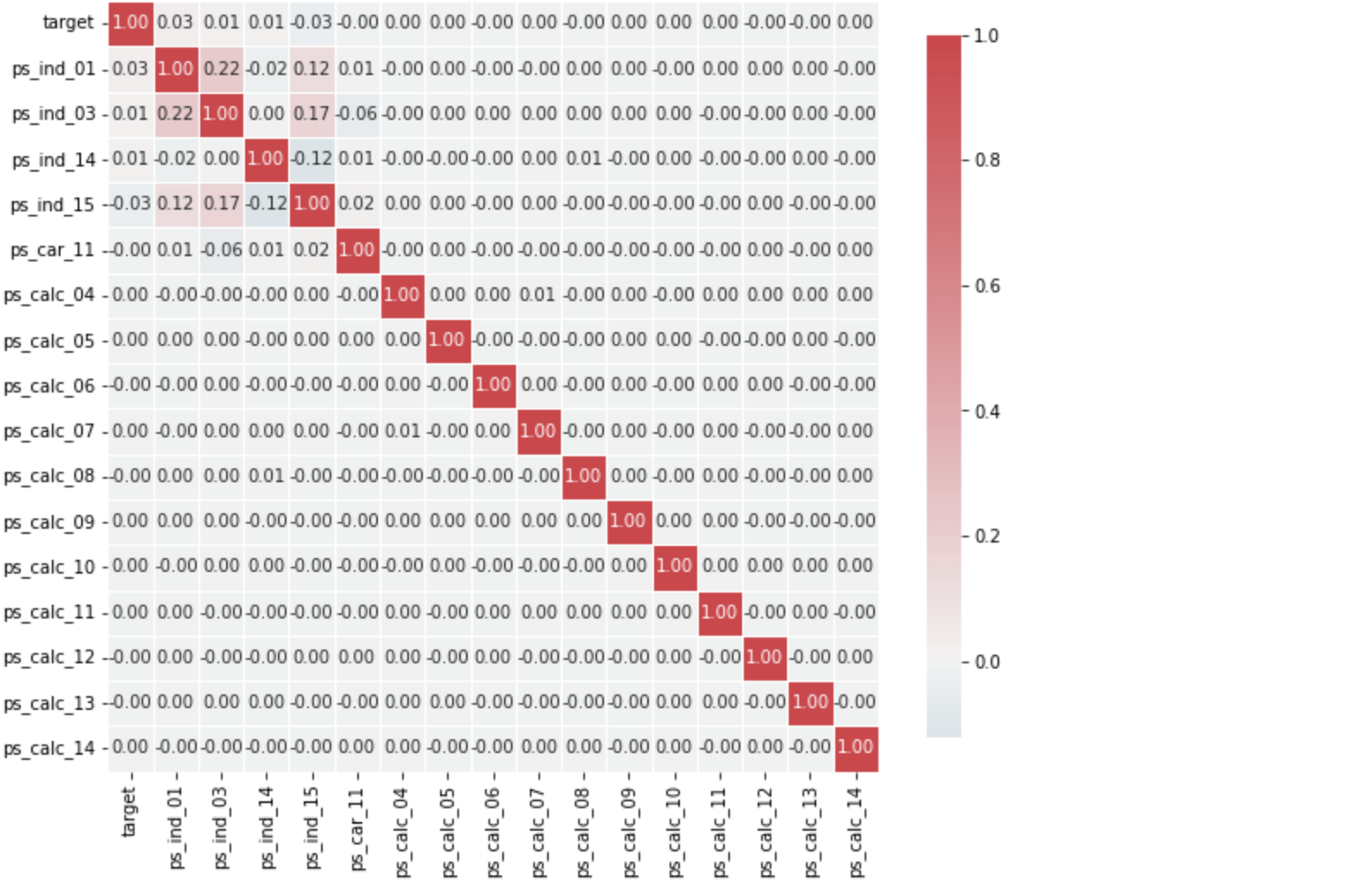

• 순서형 변수는 변수간에 큰 상관관계를 보이지 않음

3. Feature Engineering

• 위에서 가장 많은 unique 값을 갖는 범주형 변수에 대해 mean-encoding
• 나머지 변수들은 one-hot encoding 통해 더미화

Nominal = meta[(meta['level'] == 'nominal') & (meta['keep'])].index
print('One-hot Encoding 전 train 데이터 셋 변수: {}개'.format(df_train.shape[1]))
df_train = pd.get_dummies(df_train, columns=Nominal, drop_first=True)
df_test = pd.get_dummies(df_test, columns=Nominal, drop_first=True)
print('One-Hot Encoding 후 train 데이터 셋 변수 개수: {}'.format(df_train.shape[1]))

1. 교호작용 변수 생성(Interaction variables, 중요변수끼리의 곱)

• PolynomialFeatures 사용하여 교호작용 변수 생성
• 입력값 x를 다항식으로 변환
• poly.get_feature_names를 통해 feature의 이름 지정

Parameter
1. degree : 차수
2. interaction_only : 상호작용 항 출력(x1,x2일 때 자신의 제곱항 무시하고 x1x2만 출력)
3. include_bias : 상수항 생성 여부

Interval = meta[(meta['level'] == 'interval') & (meta['keep'])].index

poly = PolynomialFeatures(degree=2, interaction_only=False, include_bias=False)
interactions = pd.DataFrame(data=poly.fit_transform(df_train[Interval]), columns=poly.get_feature_names_out(Interval))
interactions.drop(Interval, axis=1, inplace=True)

# 새로 만든 변수들을 기존 데이터에 concat
print('Interaction value 생성 전 train 데이터 셋 변수 : {}개'.format(df_train.shape[1]))
df_train = pd.concat([df_train, interactions], axis=1)
df_test = pd.concat([df_test, interactions], axis=1)
print('교호작용 변수 생성 후 train 데이터 셋 변수 개수: {}'.format(df_train.shape[1]))