[Python] G4_1197_최소 스패닝 트리 ⏳

Sangho Han·2023년 6월 22일

Graph Kruskal Algorithm UnionFind 그래프 유니온파인드 최소 스패닝 트리 최소 신장 트리 크루스칼 알고리즘

🧐 Kruskal Algorithm?

💻 과정

백준 문제 풀이_유니온 파인드

목록 보기

2/9

https://www.acmicpc.net/problem/1197

문제

그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.

최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.

입력

첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.

그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.

출력

첫째 줄에 최소 스패닝 트리의 가중치를 출력한다.

예제

조건

시간 제한: 1초

메모리 제한: 128MB

🔔 최소 신장 트리(MST) 문제를 해결하기 위해서는, 우선 크루스칼 알고리즘에 대한 학습이 필요하다.

🧐 Kruskal Algorithm?

그래프에 있는 모든 노드들을 최소한의 가중치 합으로 연결하기 위해 사용됨
보통 정점, 간선, 가중치를 차례로 입력받게 됨
모든 노드들을 포함하고 사이클이 없는 연결 선을 그렸을 때, 최소 가중치의 합을 구할 수 있음

💻 과정

크루스칼 알고리즘은 그리디의 일종으로, 우선 가중치를 오름차순으로 정렬함

가중치가 낮은 순으로 차례로 노드들을 연결하는데, 사이클이 생긴다면 연결하지 않음

이 과정에서 Union Find를 이용할 수 있음
두 노드의 부모 노드가 다르다면, 연결을 해도 사이클이 생기지 않으므로 연결하고 가중치를 더해줌
그러나 부모 노드가 같다면, 이미 같은 그룹내에 있는 것이기에 연결을 하면 사이클이 생겨남

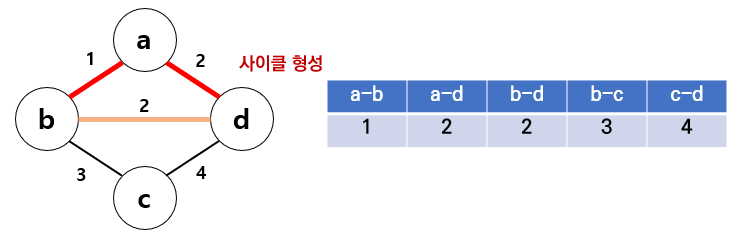
위 그림처럼 (a-b)와 (a-d)가 연결된 상태에서, (b-d)를 연결하게 된다면 (a,b,d)라는 사이클이 생겨나 최소 신장 트리가 성립할 수 없게 됨

b와 d는 a라는 동일한 부모 노드를 갖고 있으므로, 연결(union)해주지 않고 넘어가면 됨

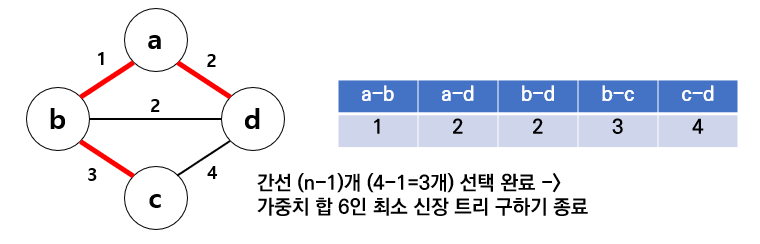
다음으로 b와 c는 부모 노드가 다르므로, union을 통해 연결해주고 가중치를 더해줌

최소 신장 트리의 간선 개수는 (노드의 개수 - 1)이므로, 선택이 완료되면 종료해줌

코드

import sys
input = sys.stdin.readline

# Union-Find
def find(x):
    if parent[x] == x: 
        return x
    return find(parent[x])

def union(a,b):
    a = find(a)
    b = find(b)
    
    if a < b:
        parent[b] = a
    else:
        parent[a] = b

# Main      
V,E = map(int,input().split()) # 노드, 간선의 개수
paths = []  # 간선 리스트
parent = list(range(V+1)) # 부모 노드 테이블
for _ in range(E):
    paths.append(list(map(int,input().split())))
paths.sort(key = lambda x : x[2]) # 가중치를 오름차순으로 정렬

MinWeight = 0
for path in paths:
    a,b,w = path[0],path[1],path[2] # 출발 노드, 도착 노드, 가중치
    # 부모 노드가 달라, Union해도 '사이클'이 생기지 않는 경우
    if find(a) != find(b):
        union(a,b)
        MinWeight += w

print(MinWeight)