로지스틱 회귀와 MSE 그리고 non-convex ?

(로지스틱 회귀에 대한 기본적인 내용을 모른다면 다음의 링크를 참고하여 공부하고 오면 된다.)
https://wikidocs.net/57805 (Pytorch로 시작하는 딥러닝 입문)

로지스틱 회귀 (logistic regression)를 공부하다 보면 다음과 같은 이야기를 반드시 보게 된다.

로지스틱 회귀의 손실 함수(loss function)으로 평균 제곱 오차 (Mean Square Error)를 사용하게 되면 non-convex 형태의 그래프가 나오기 떄문에 Mean Square Error를 사용하지 않는다.

그리고 그림으로는

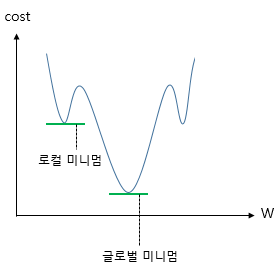
(출처ㅣhttps://wikidocs.net/57805)

이와 같은 그림을 많이 보게 된다.

(여기서 convex function의 개념을 모르면 다음 링크를 참고하면 된다.)
https://blog.naver.com/sw4r/221148661854

결국 저런 형태가 되기 때문에 gradient descent 알고리즘을 사용하였을 때 local minimum 에 갇히게 될 수 있다는 건데, 저 그래프가 어떻게 얻어지는지에 대한 설명은 보기 어려웠다.

그래서 아래의 사이트를 활용하여 직접 그려보기로 하였다.

https://www.desmos.com/calculator/ifg3mwmqun?lang=ko

이는 웹에서 편하게 그래프를 그려볼 수 있는 함수이다.
수식도 우리가 일반적으로 수식을 치듯이 작성하면 손쉽게 작성할 수 있다.

대신 x축으로 활용할 변수명은 반드시 x를 사용하여야 한다.

일단 나는 sample 및 라벨을 다음과 같이 정의하였다.

x = [1],[2],[3],[4],[5] => 정답 라벨은 0
x = [6],[7],[8],[9],[10] => 정답 라벨은 1

그리고 b를 0으로 가정하였을 때, 위의 10개의 샘플에 대해 계산한 Mean Square Error 식은 다음과 같다.

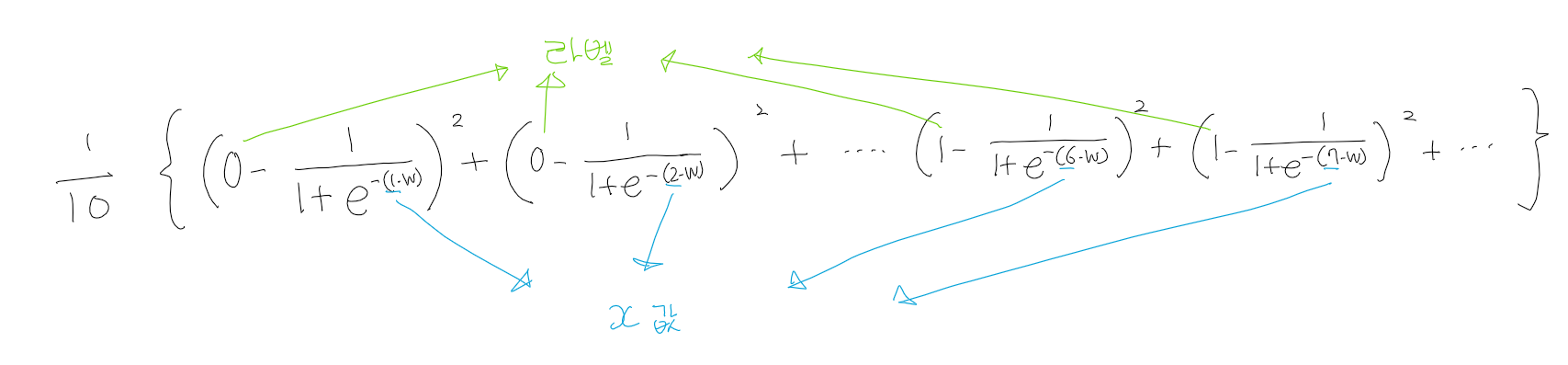
여기서 곱해진 10분의 1을 생략하고 그래프를 그렸더니 다음과 같은 그래프를 얻을 수 있었다.

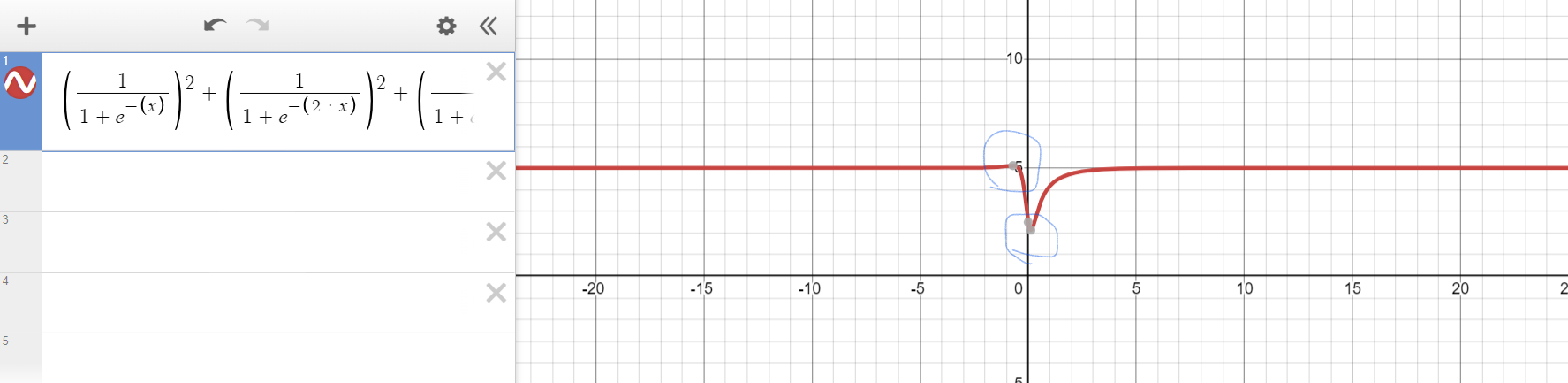
여기서 왼쪽의 파란 동그라미를 주목하자.
저 부분의 살짝 튀어나와있기 때문에 gradient descent 알고리즘을 적용할 시에 w의 초기값이 대략 0.26 미만이면 global minimum 을 찾지 못하게 된다.

맨 위의 그림처럼 교과서에 나올 것 같은 non-convex function은 아니지만, convex function은 아님을 확실히 알 수 있다.

이렇듯 예시를 통해 MSE를 쓰면 안되는 이유를 알았다.
그럼 cross entropy는 왜 가능할까?

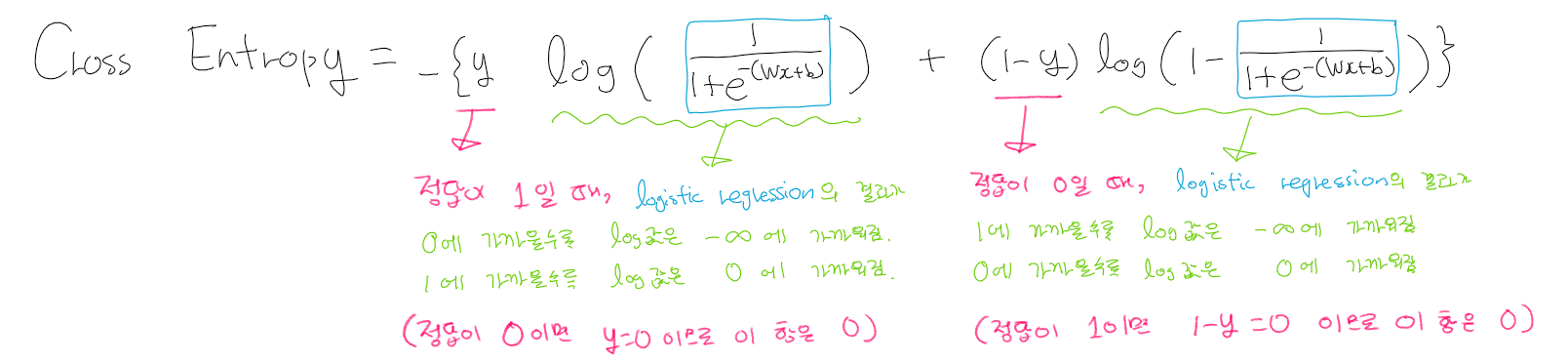
sample 1개에 대한 cross entropy는 위와 같이 계산할 수 있다.

이 식은 오차가 클수록 -무한대에 가까워지고 작을 수록 0에 가까운 값을 가지는데 loss는 양수의 값을 가져야 하므로 마이너스를 붙인다.

더 정확하게 설명하자면 gradient descent 알고리즘에 의해 최소의 값을 가지는 x값(정확히는 매개변수값)을 찾아야 하는데, 이 식에서는 마이너스 무한대 에 가까울수록 즉, 작아질수록 오차가 커지므로, 이 식에 마이너스를 취해야 비로소 loss식으로 사용이 가능하다.

저렇게 계산할시 위에서 얘기한 샘플에서 loss 식은 다음과 같다.
(앞에 곱해지는 상수항은 제외하였다.)

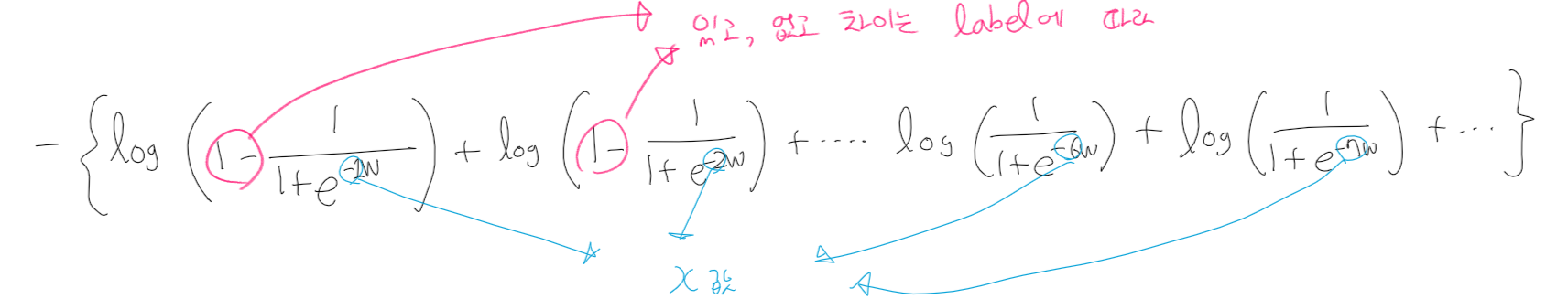
이 식으로 그래프를 그리면 다음과 같다.

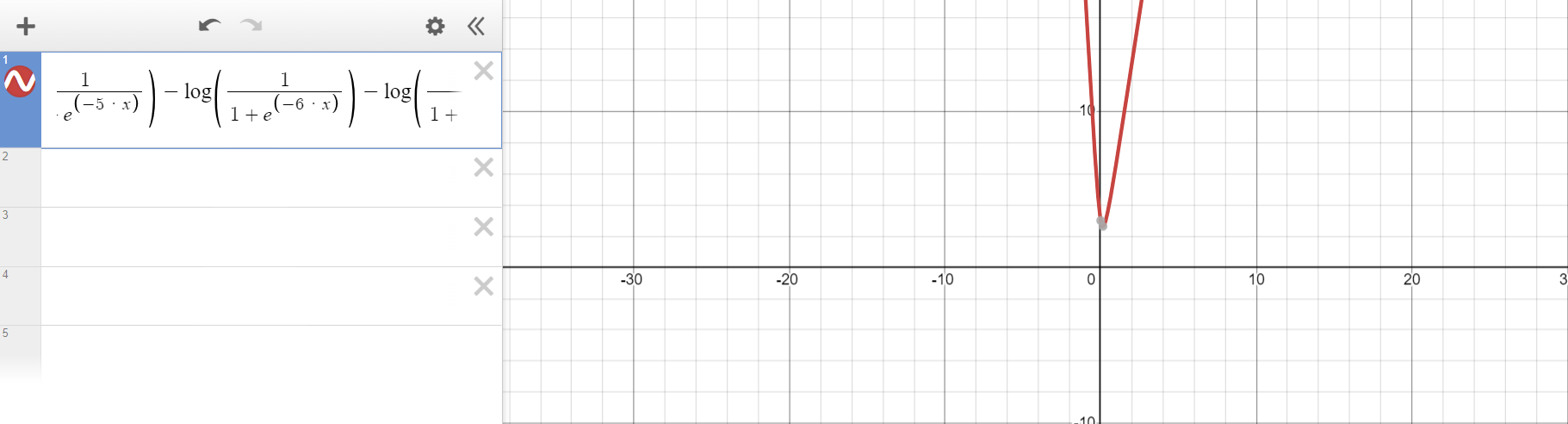
라벨이 0인 항 또는 1인 항만 존재할 때는, 일반적인 로그함수의 식과 똑같은 모양을 보여주다가 라벨이 0인 항과 1인 항이 함께 존재하면서 저렇게 convex function의 형태를 보인다.

이것이 가능한 이유는 라벨이 0인 항을 모두 더한 함수가 단조 증가이며 치역이 양수, 라벨이 1인 항을 모두 더한 함수가 단조 감소이며 치역이 양수인 함수이기 때문입니다.

이 글이 나와 같이 logistic regression 에 loss function을 써야 하는 이유에 대한 직관적인 이해를 필요로 하는 사람들에게 도움이 되었으면 한다.