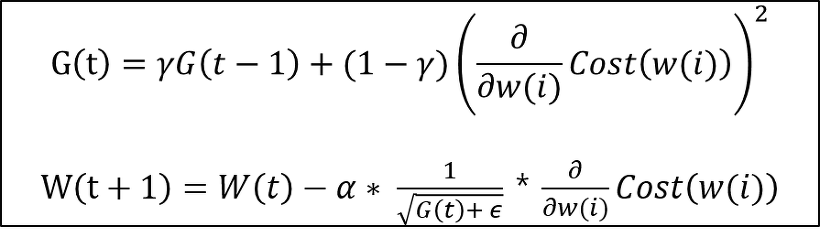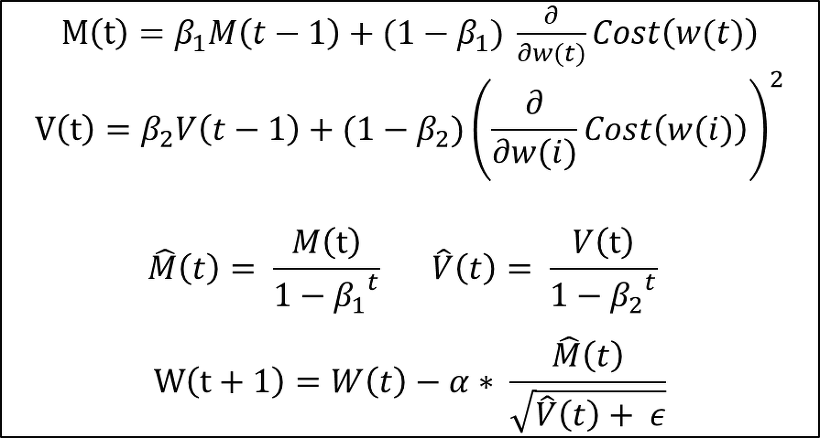Optimizer

• loss 가 가장 작아지는 지점을 찾는 방법

Gradient Descent

• 함수의 기울기 를 구하여 함수의 극값에 이를 떄까지 기울기가 낮은 쪽으로 이동하는 방법

$W(t+1) = W(t) - α * ∂/∂w * Cost(w)$

learning rate

• 경사 하강법에서 얼만큼 이동할것인지에 대한 정보
• 경사 하강법에서 learning rate = α 이다.

Momentum (관성)

• 이전에 이동했던 방향을 기억해서 다음 이동 의 방향에 반영
• 이전에 이동했던 방향에 관성 값을 넣어주는것이다.

$V(t) = m * V(t-1) - α * ∂/∂w * Cost(w)$
$W(t+1) = W(t) + V(t)$

Local minimum , Global minimum

• loss 값이 가장 작은곳 -> global
• loss 값이 구간 안에 작은곳 -> Local

Adagrad (Adaptive Gradient)

• 많이 이동한 변수는 최적값에 근접했을 것이라는 가정하에 많이 이동한 변수를 기억해서 다음 이동의 거리를 줄인다.

• G(t) 값이 커지면 이동거리가 짧아진다.

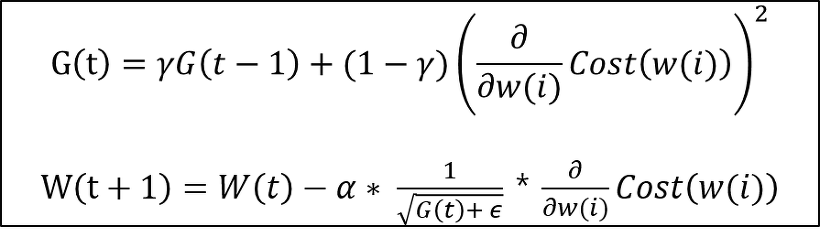
Adam

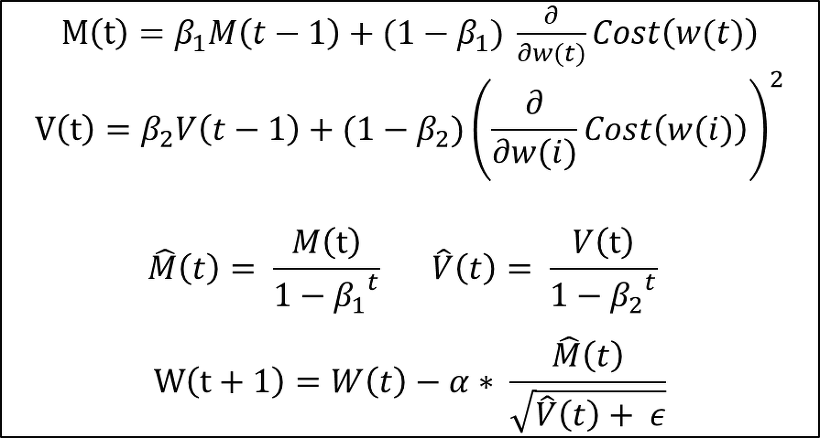
• 이동을 할떄 M 만큼 이동을 하고 V 로 나눠준다.

Vanishing Gradient

• sigmoid 같은 함수는 값이 변화가 거의 없다 따라서 Hidden Layer 를 많이 만들어도 가중치의 변화가 없다.

실습

import pandas as pd
import tensorflow as tf
path = "https://raw.githubusercontent.com/blackdew/ml-tensorflow/master/data/csv/boston.csv"

data = pd.read_csv(path)
data.head()

x = data[['crim', 'zn', 'indus', 'chas', 'nox', 'rm', 'age', 'dis', 'rad', 'tax',
       'ptratio', 'b', 'lstat']]

y = data[['medv']]

X = tf.keras.Input(shape = [13])
H = tf.keras.layers.Dense(32 , activation = "swish")(X)
H = tf.keras.layers.Dense(32 , activation = "swish")(H)
H = tf.keras.layers.BatchNormalization()(H)
Y = tf.keras.layers.Dense(1)(H)
model = tf.keras.Model(X,Y)
model.compile(loss = 'mse')

model.summary()


loss = tf.keras.losses.MeanSquaredError()
optim = tf.keras.optimizers.Adam(learning_rate = 0.001)
for e in range(1000):
  with tf.GradientTape() as tape:
    pred = model(x.values,training = True)
    cost = loss(y,pred)
  grad = tape.gradient(cost,model.trainable_variables)
  optim.apply_gradients(zip(grad,model.trainable_variables))
  print(e,cost)
  
 model.evaluate(x,y,batch_size = 128)