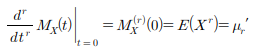📌 적률생성함수

💡 확률변수 X의 원점에 대한 r차 적률(moment)

• 확률 변수 $X^r$의 기대값 $E(X^r)$를 확률변수 X의 원점에 대한 r차 적률이라고 하고 이를 $u_{r}^{'} = E(X^r)$로 표기

• 

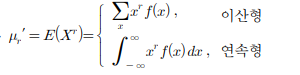
• $u_{r}^{'} = E[(X-u)^r]$ : 평균 u에 대한 r차 중심적률이라 정의

💡 적률생성함수 $M_x^{(t)}$

• 확률변수 X의 적률생성함수 $M_x^{(t)} = E(e^{(tX)})$

• 

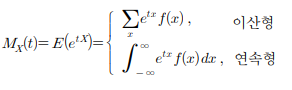
💡 적률생성함수로 r차 적률 구하기

💡 적률생성함수 성질

• 확률 변수 X와 Y가 같은 적률생성함수를 가지면, 즉 모든 t에 대해 $M_x^{(t)} =M_y^{(t)}$이면 두 확률 변수는 동일한 분포를 가진다.
  이 성질을 통해 베르누이 분포가 반복되면 이항 분포임을 증명할 수 있다.

참고
https://www.youtube.com/watch?v=6carocrozCU
https://blog.naver.com/mykepzzang/220846464280