[자료구조] 비선형 자료 구조

1. 비선형 자료구조란?

일렬로 나열하지 않고 자료 순서나 관계가 복잡한 구조를 말하며, 대표적으로 트리와 그래프를 다루고자 한다.

2. 그래프

1) 그래프의 특징

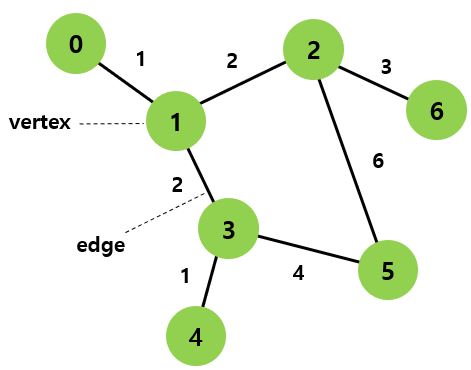
① 정점(vertex)과 간선(edge)으로 이루어진 자료구조를 말한다.

• 정점(or 노드)
  : 데이터를 나타내는 요소
• 간선
  : 정점들을 연결하는 선으로 방향성을 가지는지 여부에 따라 방향 그래프와 무방향 그래프가 결정됨

② 그래프는 정점과 간선의 조합으로 이루어지며, 정점들이 간선에 의해 연결되어 그래프를 형성

2) 그래프의 구현

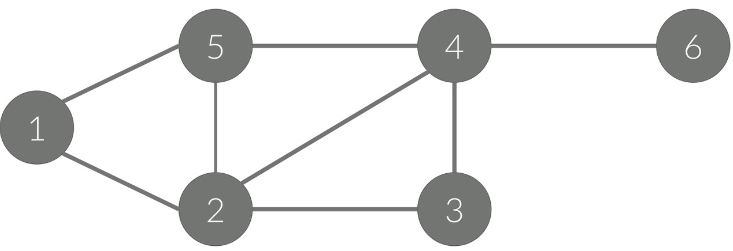
• 정점 : {1,2,3,4,5,6}
• 간선 : {(1,2),(1,5),(2,3),(2,4),(2,5),(3,4),(4,5),(4,6)}

① 인접 행렬 (Adjacency - matrix)
정점의 개수(V)를 가지고 V x V 이차원 배열을 생성

int graph[6][6];
/*
i행j열 : i행 -> j열로 간선이 존재하면 (1), 존재하지 않으면(0)
010010
101110
010100
011011
110100
000100
*/

② 인접 리스트
벡터(vector)를 이용해 구현
(연결 리스트를 이용해 구현할 수 도 있음)

#include <vector>
vector<int> adj[6];
/*
adj[1] = {2,5}
adj[2] = {1,3,4,5}
adj[3] = {2,4}
adj[4] = {3,5,2,6}
adj[5] = {1,2,4}
adj[6] = {4}
*/

3. DFS와 BFS

그래프 자료구조와 자주 사용되는 알고리즘으로 DFS와 BFS가 있다.

• 둘 다 Search 알고리즘의 일종으로 그래프 자료 구조의 모든 원소를 탐색하는 알고리즘이다
• DFS와 BFS의 주요한 차이는 그래프에서 어떤 원소를 먼저 탐색하는 가 이다.

1) DFS(Depth First Search)

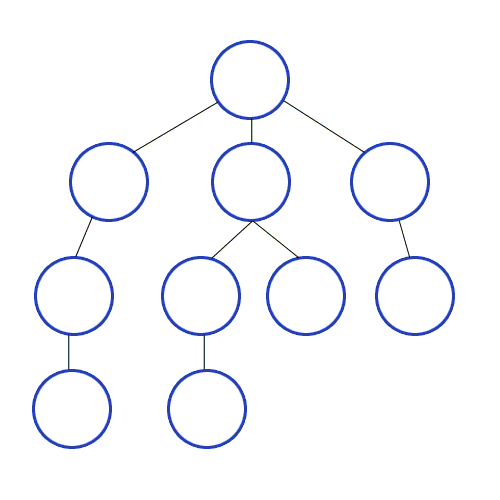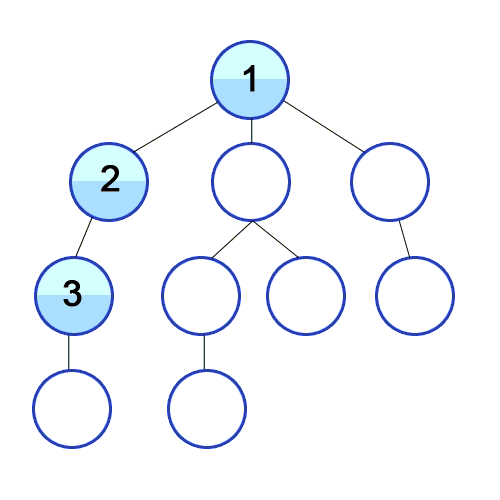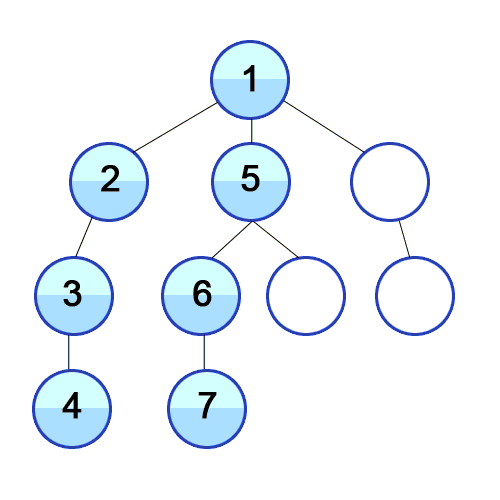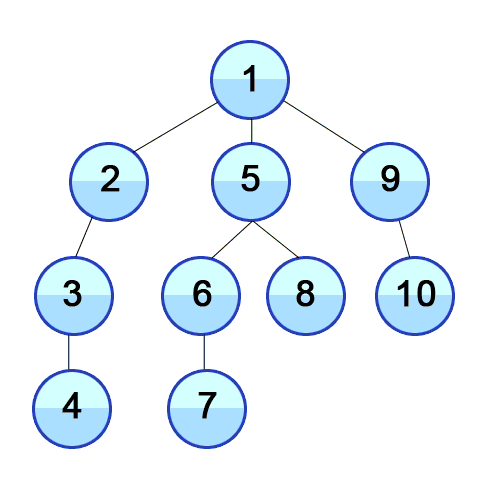
① 하나의 가지를 모두 탐색한 이후 다음 가지를 탐색

② 깊이 탐색하는 방법

// v: 정점 e: 간선
int v,e;
// 인접 리스트
vector<vector<int>> graph;
// 방문 여부
vector<bool> isVisited;

void DFS(int cur){
	// 현재 방문한 노드 표시
	isVisited[cur]=true;
    
    // 현재의 정점과 간선으로 연결되어 있는 모든 정점을 순회
    for(int i=0;i<graph[cur];i++)}
    	int next = graph[cur][i];
        if(!isVisited[next]){
        	DFS(next);
        }
    }
}

// 정점과 간선을 입력받아 인접 리스트로 저장
int main(){
	cin>>v>>e;
    graph.assign(v+1,vector<int>(0,0));
    for(int i=0;i<e;i++){
    	int s,e;
        cin>>s>>e;
        graph[s].emplace_back(e);
        graph[e].emplace_back(s);
    }
}

2) BFS(Breadth First Search)

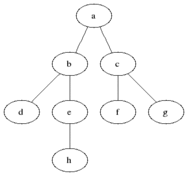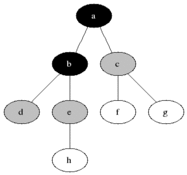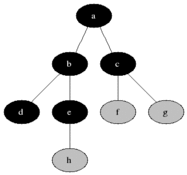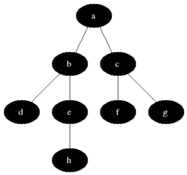
① 현재의 노드에서 가장 가까운 노드부터 우선적으로 탐색하는 알고리즘
② 큐를 사용하여 구현

// v: 정점 e: 간선
int v,e;
// graph[1] = 1번 노드와 연결된 정점들
// graph[2] = 2번 노드와 연결된 정점들
// ... 
vector<int>graph[v];
// 정점의 방문 여부
bool isVisited[v];

void BFS(int start, vector<int>graph[],bool check[]){
	queue<int> q;
    q.push(start);
    check[start] = true;
    while(!q.empty()){
    	int tmp = q.front();
        q.pop();
        // 현재 노드와 연결된 모든 노드를 방문
        for(int i=0;i<graph[tmp].size();i++){
        	
            // 방문하지 않은 경우 방문하기
            if(check[graph[tmp[i]]==false){
            	q.push(graph[tmp][i]);
                check[graph[tmp][i]]=true;
            }
        }
    }
}


int main(){
	for(int i=0;i<e;i++){
    	int u,v;
        cin>>u>>v;
        graph[u-1].push_back(v);
        graph[v-1].push_back(u);
    }
    for(int i=0;i<n;i++){
    	sort(graph[i].begin(),graph[i].end());
    }
	return 0;
}