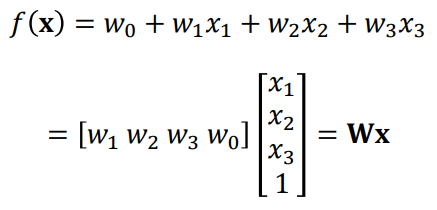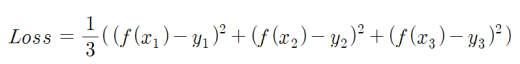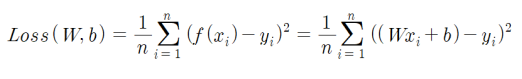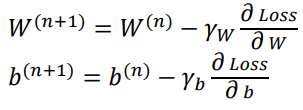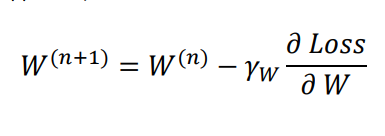Linear Regression Model

1. 머신러닝이란?

1) Machine learning Introduction

① 심플한 정의를 내리자면

• 입력 값에 대한 출력 값을 계산하는 함수를 만드는 것.
• 입력 값(이미지, x)에 대해 출력 값(강아지, 차,, 등 y)의 bounding box를 찾는 것

② Segmentation도 마찮가지로, 입력 이미지로부터 세그멘테이션 결과(출력)을 얻는 것.

③ Image Caption 또한 입력 이미지로 부터 설명(caption)을 생성

<> Caption to Image : Caption 입력을 토대로 이미지를 생성
등등

2) VQA (Visual Question Answering)

: 이미지와 질문을 주면, 이미지를 토대로 답변을 생성

3) Application of ML

① 자율 주행
: 카메라 영상, 속도 데이터등을 토대로 자율 주행

② 암 진단
: 의료 데이터(CT,MRI,X-ray등)을 토대로 암 진단

결론적으로, 머신 러닝이란 "함수 찾기". 이때의 함수란 입력 데이터에 대해 결과값을 출력해내는 함수이다.

2. Challengo for ML

• 그렇다면 이러한 "함수 찾기"는 쉬운 일이 아니다. 컴퓨터는 이진 형식으로만 데이터를 분석할 수 있으며, 이로부터 유의미한 분석을 통해 원하는 결과물을 내는 함수를 찾는 것은 매우 복잡한 일이다.

Topic for this point is then..
: How to find a proper/learn the function that does mapping from input to output?

• Key is how to find f(x) especially using DL
• brain already knows the function!
• 정확한 함수를 찾는 것보단 뇌가 할 수 있는 함수를 "모방", "근접"한 함수를 찾는 것.

ⓐ 함수 찾기
ⓑ 현실 세계의 문제를 어떻게 포맷팅해서 함수를 적용하는가

3. ML / DL

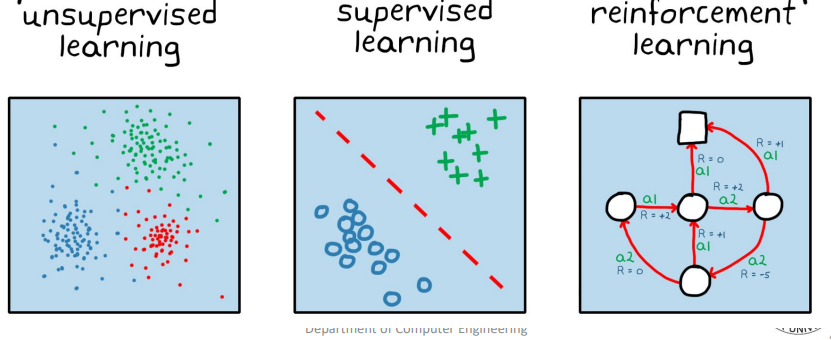
1) Types of Learning

① Supervised Learning : 입력과 출력 데이터셋이 주어짐. 즉 a입력에 대해 어떤 출력(labe)이 나와야하는지 이미 정해짐

• 심플하고 명확한 세팅이지만 현실적으로 드믄 시나리오임.
• 사실 (특히 의료 영상 분야)에서 모든 입력에 대해 정확한 라벨링을 알고 있는 것은 현실적으로 어려움

② Unsupervised Learning : 입력 데이터에 대해 결과값은 모르는 상태에서 f(x)를 구할 때 (=학습할 때)

③ Weakly/Semi-superviesd : 일부만 라벨이 존재 or 이미지(입력)과 라벨 셋이 1개만 존재하는 상황

④ Reinforcement : 액션(의 결과)에 대해 보상을 부여함으로써 목적에 가까운 액션에 대해서는 강화하는 방향으로 학습

• 위의 타 학습과는 결이 좀 다름(활발히 사용되고 있지는 않음)

4. Linear Regression(선형 회귀 분석 기법)

1) Linear Method

① 무작정 f(x)를 찾는 대신 틀을 먼저 잡는 것.
② 그 틀(frame)중 하나가 linear 모델

f(x) = wx + b

③ x,y를 토대로(학습) w(기울기)와 b(y절편) 탐색하여 점차 데이터와 가까운 직선을 찾는 것

2) Regression & Classification

① Regression (회귀)

• 데이터의 트렌드를 따라가는 선을 찾는 것.

② Classification (분류)

• 두 가지를 나눌 수 있는(구분 짓는) 선을 찾는 것.

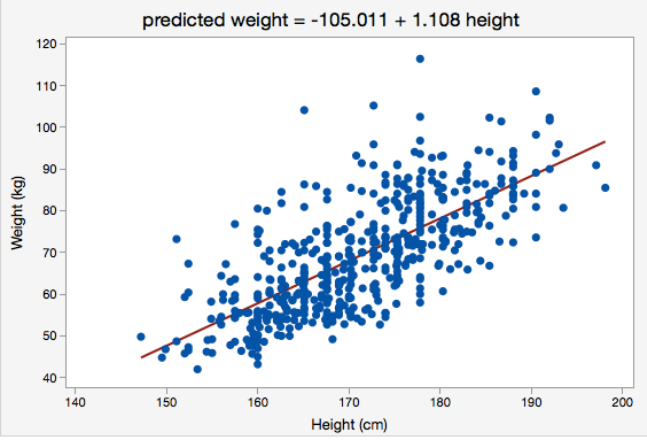
3) Linear Regression

: 직선 or 평면 모양이며, 데이터의 트렌드를 따라가는 것을 찾는 모델

• 데이터의 트렌드를 따라가기 위해 w(기울기)와 b(y절편,bias)값을 근사해나가는 것을 학습이라 한다.

ⓐ Single Variable Linear Regression (단일 변수 선형 회귀):
단일 변수 선형 회귀는 하나의 독립 변수 (입력 변수)와 하나의 종속 변수 (출력 변수 또는 예측 대상) 간의 관계 모델링 기술

• 이 모델은 간단한 직선의 방정식을 사용하여 관계를 설명합니다. 예를 들어, 주택 가격을 예측하기 위해 집 크기(면적)만을 사용하는 경우, 주택 가격 = (집 크기 * 기울기) + 절편과 같은 방정식을 사용할 수 있습니다.

ⓑ Multivariate Linear Regression (다중 변수 선형 회귀):
다중 변수 선형 회귀는 여러 독립 변수(입력 변수)와 하나의 종속 변수(출력 변수 또는 예측 대상) 간의 관계의 모델링 기술

• 이 모델은 각 독립 변수의 가중치(계수)를 고려하여 복잡한 관계를 설명합니다. 예를 들어, 주택 가격을 예측하기 위해 집 크기, 침실 수, 욕실 수, 지역 인구 등 다양한 변수를 사용할 수 있습니다. 모델은 주택 가격 = (집 크기 가중치1) + (침실 수 가중치2) + (욕실 수 * 가중치3) + ... + 절편과 같은 방정식을 사용합니다.

4) General Form

f(x) : 종속 변수 (예측하려는 값)
y : 실제 데이터. f(x)는 y값에 근사하게 예측될수록 성능이 좋은 것
x1,x2...,xn : 독립 변수 (특징 또는 설명 변수)
w1,w2...,wn : 회귀 계수이며, 이들은 선형 모델의 파라미터로서 학습되어야 하는 값

• 입/출력 차원에 따라 일반화된 형태를 만들 수 있음
• 가령 입력이 1개가 아니라 자동차 (50 pixel x 50 pixel x 3rgb)=7500 차원이라면?
  -> matix(w)와 data(vector)의 곱으로 나타낼 것

※ 용어 정리 : f(x)(prediction, 직선의 함수0 와 y(실제 데이터)를 구분하여 사용

f(x) = wx + b 에서 w,b를 알려면 데이터가 2개면 된다?

: 수학적으론 yes지만, 머신러닝에서는 no!

• 머신러닝의 데이터는 "노이즈"가 존재하므로, 트렌드는 있지만 정확하지는 않으므로 단 2개만으로 직선을 그으면 데이터의 트렌드와 거리가 먼 직선이 나올 수 있다. 따라서 머신러닝에서는 가능한 데이터가 "많을 수록" 좋다!

요약하자면, 데이터의 트렌드를 따르는 근사한 직선을 찾는 것이 목표이며, 모든 데이터를 정확히 지나는 (피팅되는) 선을 찾는 것은 아니다.

• $(y-f(x))^2$ 을 최소로 하는 것이 목표

5) Loss Function

① Loss 계산

② Generalization(using sigma)

③ Loss(W,b)를 2차원 평면에서 최솟값 계산

• w기준, b기준으로 2차 함수를 그린 후 각자의 최소값을 만족하는 w와 b를 구함
• 완전제곱식 변환후 최소의 w와 b를 찾는 것 or 미분해서 0나오는 값 찾기

Summary. 에러의 크기를 구하는 함수(Loss Function)

• 에러(=예측값과 실제출력의 차)의 제곱의 합
  loss function의 min value가 최소가 되는 w와 b를 구하는 것이 핵심

※ 간단한 선형 모델은 위와 같이 풀리지만, 복잡한 모델(고차 방정식, sin or cos 함수)의 경우 최소를 만드는 w,b를 구하는 것이 불가능에 가까움
-> Gradient Descent : more general form for this case

5. Gradient Descent

: practical approach for linear regressiong model

1) idea of gradient descent(=경사 하강 기법)

즉 점차 하강을 통해 loss 값이 최소가 되는 w와 b를 찾아내는 기법이다. 이를 사용하는 이유는 loss function의 미분값을 구하기 어려운 식이 대부분이기 때문ㅇ디ㅏ.

• Update Rule
  

위 규칙을 토대로 W(n+1)을 구하면 다음과 같다.

이때 𝛾𝑊 는 학습 률이다.

b(n+1)도 W(n+1)과 마찮가지로 (이전값-미분계수x학습률)로 계산된다.

2) Learning Rate

이때 적절한 학습률을 설정해야 loss값이 최소가 되는 w와 b를 제대로 구할 수 있다.
만일 학습률이 너무 작다면, 최소값에 도달하는 데 너무 오랜 시간이 걸린다.
만일 학습률이 너무 크다면, 빠르게 진동하여 발산할 수 있다.
-> 적당해야한다.

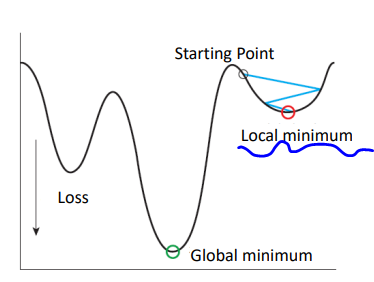
3) Local Minima Problem

이러한 Gradient Descent 방법에도 문제점이 존재한다. 이는 부분 최솟값 이슈인데, 그림을 참고하도록 한다. Gradient Descent 기법을 사용할 때 시작 위치를 어디로 설정하느냐에 따라 전체 loss function의 최솟값이 아닌 부분 최솟값을 찾아내는 경우가 존재한다. 이는 우리가 찾고자 하는 loss값을 최소로하는 최적의 W와 b를 찾는 것과는 다른 값을 찾아낸다.