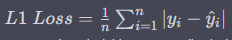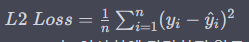0918 - week3
1. Linear Classification
머신러닝이란 입력에 대한 출력 데이터를 매핑하는 함수를 찾는 것
ⓐ 함수를 지정한 후
ⓑ 함수의 파라미터를 적절히 학습할 것
1) Loss Function
- 함수를 지정한 후 입력에 대한 예측 값(f(x))을 찾고, 실제값(y)과의 차이(eror)를 구한 후 그 합을 계산하는 함수
- loss(sum of error)를 최소로 하는 w(파라미터)를 찾도록 한다.
2) Classification(분류)
- 입력(이미지)에 대해 출력을 분류
- 가령 출력이 (강,고,소,자동차,말 : 5 classes)이라고 가정하면 출력 데이터는 5가지 중 1가지로 "분류" 될 것
e.g. 출력 데이터
<0,0,0,1,0> : 자동차로 분류된 것
<1,0,0,0,0> : 강아지로 분류된 것
위 데이터는 확률로 읽힌다. 자동차일 확률이 1(100%)이고 나머지 일 확률이 0이라고 보는 것
3) Linear Model : 선형 함수
#Basic Notation for Function
f(X;W,b) = Wx + b
- X : 입력값
- W,b : Training 할 파라미터(Matrix)
- Y : target output (Real output)
- f(X) : 예측 값
4) Example (11p)
X = {0.1,1.5,0.07,2.32} : simplified input
f(x; W,b) => 자동차의 값이 제일높으므로 자동차로 분류
2. Loss Function
가장 분류를 잘하는 W,b를 찾기 위해 Loss Functionh을 구성
28p : 왼쪽(w1)이 더 좋아 보이는데 왜? 객관적으로 얼마나 더? 좋은가
-> Loss Function을 통해 설명할 수 있음
① L1 Loss :예측값과 실제 값 사이의 차이의 절대값
② L2 Loss(MSE Loss) : 예측값과 실제 값 사이의 차이를 제곱
1) Norms
: vector의 크기
① 우리가 일반적으로 알고 있는 vector의 크기 = L2-Norm
② Lp-Norm =
③ 가장 많이 쓰는 것은 L1,L2
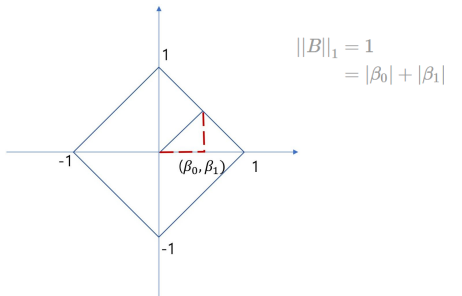
- L1-norm과 L2-norm을 도식화하면 다음과 같이 이해해볼 수 있다.
- L1-norm
- L2-norm
2) Loss with Norm
Norm을 이용해 Loss를 구성(36p)
ⓐ Y-f(X) = error
ⓑ error(vector)의 크기를 구함 (Norm을 이용)
ⓒ L2 loss는 일반적으로 제곱을 벗겨서 사용(루트계산보다 심플하므로) = MSE Loss (37p 표기법 확인)
ⓓ 시그마를 사용해 모든 데이터에 대한 loss값을 더함
(39,40p : W에 대한 함수)
3) Example
43p
Loss가 더 작은 W를 찾기 (L1, L2 Norm에 따라 답이 바뀐다) ※
4) ★ Overfitting vs Underfitting
45p
① Underfitting 이란? (모델 복잡도 < 데이터복잡도)
너무 간단한 모델을 사용(가령 선형 모델)을 사용하면 실제 데이터의 근접할 수 없음
즉, 모델 복잡도와 데이터의 복잡도를 충분히 고려해야한다.
② Overfitting 이란? (모델 복잡도 > 데이터 복잡도)
너무 복잡한 모델(100차 방정식)을 사용해도 실제 데이터와 근접할 수 없음
즉 모든 데이터에 Loss가 0이 되버릴 수 있으며 이는 "예측"이라는 애초의 목적에 벗어나는 방향이다.
모델 복잡도 = 파라미터의 개수
즉, 모델이 복잡하다는 것은 파라미터(W)가 많다는 것과 같은 컨셉으로 이해하면 된다.
(가령 Linear Model은 W,b : 2개의 파라미터가 존재, n차 방정식은 n+1개의 파라미터가 존재)
5) Regularization
위와 같이 오버피팅/언더피팅을 방지하기 위해 사용하는 방식, Ockham's razor은 데이터를 설명할 수 있는 커브 중 가장 심플한 커브가 정답이라고 보는게 타당하다는 관점
47p
Regularization
= L(W) 함수에 Regularization을 추가하여 데이터를 너무 따라가지 않도록(즉 Loss가 0이 되는 것을 막도록) 방해하는 역할
R(W) = W의 제곱 or L1 (일단 패쓰)
결론은 Loss Function을 구성하고, 적절한 fitting을 위해 (over fitting 방지) 텀(Regularazation)을 추가할 수 있다. 이떄 Loss를 최소화하는 W를 찾는 것이 목표임을 계속 기억하도록 한다.
3. How to find W
1) Random Search
: w를 랜덤하게 바꿔가며, loss값을 비교
-> 함수의 복잡도(미분이 불가능해도) 무관하게 사용할 수 있는 방법
-> very slow(노가다 방식)
2) Analytic Solution
: 미분해서 0이 되는 w값을 찾기
-> Linear Model같이 심플한 함수에 대해서만 가능(즉 제한적인 방식이다)
3) Numerical Solution : GCD (Gradient Descent)
: 미분해서 반대방향으로 계속 이동하며 찾아가는 방식
-> 일반적인 방법으로 활용될 수 있다
-> 물론 이 방식도 미분이 가능한 함수에만 적용 가능하다.
(* 따라서 뉴럴 네트워크에서 심플한 함수 중첩하는 과정에서 미분이 되는 함수들만 사용함)
위와 같은 방식으로 분류를 할 수 있다.
3. Cross Entropy Loss
69P : 뉴럴 네트워크로 확장
딥러닝이 뇌를 모방하는 것이다보니 생물학적 뇌를 모방한 컨셉이 꽤 많다.
뉴런의 핵을 노드로 표현, 각 노드가 데이터를 가지고 노드간에 복잡하게 연결되어있는 구성을 시도(즉 뇌를 모방 : 76P)
-> 인공신경망은 뉴런들이 비선형적으로 연결되어 있다.
76P 선 위에 W가 존재.
ⓐ Forward Propagation
가령 자동차 이미지의 데이터(7500)개의 input 값들이 내부의 w들과 연산(심플한 함수들을 사용해 다음 레이어의 input으로 또 제공하고) 을 반복해 최종 output이 나오는 방식
ⓑ Back Propagation
미분값을 계산한 후 이를 바탕으로 w를 계속 업데이트