알고리즘 - 오일러회로(14926)

heyhey·2023년 1월 11일

목록 보기

2/9

14926 Not Equal

문제

주어진 N개의 수가 모두 서로 다르다는 것은 기호 "!="를 통해 하나의 식으로 표현할 수 있다. 예를 들어 A, B, C가 모두 서로 다르다는 것은 논리식으로 (A != B) && (B != C) && (C != A) 로 쓸 수 있고, 이를 다음과 같이 한 줄로 표현하는 것을 A, B, C에 대한 "한 줄 표기법"이라고 부르기로 하자.

A != B != C != A

하지만 5개의 수 A, B, C, D, E가 모두 서로 다르다는 것을 다음처럼 표현하는 것은 올바른 한 줄 표기법이 아니다.

A != B != C != D != E

왜냐하면 5개의 수가 서로 다름을 나타내기 위해서는 10개의 쌍에 대해 서로 다름을 표현해야 하고, 이는 적어도 10개의 "!="를 필요로 하기 때문이다. 일반적으로 주어진 N개의 수가 모두 다름을 한 줄 표기법으로 표현하기 위해서는 적어도 C(N, 2)개의 "!="이 필요함이 알려져 있다(C(N, 2) : N개의 서로 다른 대상 중 2개를 뽑는 가짓수).

홀수 자연수 N이 주어졌을 때, N개의 수 a1, a2, …, aN에 대해 가능한 한 줄 표기법 중 가장 짧으면서 사전순으로 가장 앞에 오는 한 줄 표기법을 출력하는 프로그램을 작성하라. 단 이때 "!="은 공백으로 대신하기로 한다. 예를 들어 N = 3이 주어졌을 때 "a1 a2 a3 a1"는 정답으로 인정되지만, "a3 a1 a2 a3"는 사전순으로 앞의 표기법보다 뒤에 오기 때문에 올바른 한 줄 표기법이라도 정답으로 인정되지 않는다.

Hint : 한 줄 표기법에 최소로 필요한 "!="의 개수인 C(N, 2)는 Vertex가 N개인 완전 그래프의 Edge의 개수와 동일함을 고려해 보라.

예제

1 => a1 a2 a3 a1
3 => a1 a2 a3 a1 a4 a2 a5 a3 a4 a5 a1

풀이

문제가 무슨말인지 통 이해가 되지 않는다..
예제를 보며 그림을 그려보니 이해가 바로 됐다.

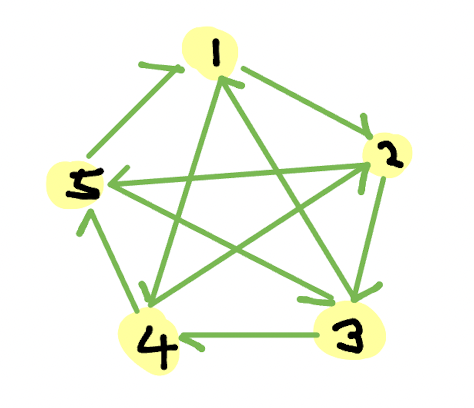
그려보니 한 붓그리기였다 =>한붓그리기를 오일러 회로라고 부른다

입력값이 홀수일 때만 한붓 그리기가 가능하다.
가장 짧은 조건은 중복된 노드가 없을 때
사전 순으로 맨 앞의 값

첫 풀이

import sys
sys.stdin = open("./2023/1월/input.txt")
sys.setrecursionlimit(10**6)

N = int(input())
graph = [[] for _ in range(N)]
graph_count = 0
for i in range(N):
  for j in range(N):
    if i!=j :
      graph[i].append(j)
      graph_count+=1

result = 99999999999999
# [[1, 2, 3, 4], [0, 2, 3, 4], [0, 1, 3, 4], [0, 1, 2, 4], [0, 1, 2, 3]]
count2 = 0
now = 0
def dfs(start_node,count,visited):
  global result
  global count2
  for number in graph[start_node]:
    if visited[start_node][number] == 0: # 방문을 안했다 
      visited[start_node][number] = 1
      visited[number][start_node] = 1
      dfs(number,count+str(number+1),visited)
      visited[start_node][number] = 0
      visited[number][start_node] = 0
      if len(count)*2 == graph_count:
        result = min(int(count),result)
        print(sort_result(result))
        exit()
        

def sort_result (result):
  r = ""
  for i in str(result):
    r += "a{0} ".format(i)
  r += "a1"
  return(r)

visited = [[0]*N for _ in range(N)]
dfs(0,"1",visited)
print(sort_result(result))

처음에는 단순한 DFS 문제인줄 알고
자리수가 N * (N-1)/2인 모든 경로를 다 구하고,
그 값이 최소값인지 모든 값들을 비교했다.
물론 답은 나왔지만 N이 499까지 구해야 하는데 이 방법은 불가했다.
(사실 11 조차 못하더라)

최종 풀이

사전 순으로 가장 빠른 것은 순서대로 노드를 진행하면서, 그 다음 노드가 지나가지 않았던 노드들 중에 가장 작은 가게 된다면 앞자리수 부터 작은 수가 쌓이게 될 것이다.

import sys
sys.setrecursionlimit(2*(10**5))

N = int(input())
graph = [[] for _ in range(N+1)]
visited = [[0]*(N+1) for _ in range(N+1)]

for i in range(1,N+1):
  for j in range(1,N+1):
    if i!=j :
      graph[i].append(j)

def dfs(start_node):
  print("a{0}".format(start_node),end=" ")
  while graph[start_node]:
    i = graph[start_node].pop(0)
    if visited[start_node][i] == 0: # 방문을 안했다 
      visited[start_node][i] = 1
      visited[i][start_node] = 1
      dfs(i)
              


visited[1][N] = 1
visited[N][1] = 1
dfs(1)
print("a1")

sys.setrecursionlimit(2*(10**5)) 이거 때문에 골치가 아팠다.

깊이가 깊어지다 보니 maximum recursion 에러로 인해 setrecursionlimit()를 적어주었다.
106 의 값으로 하게 되면 메모리 초과, 105 의 값으로 하면 다시 maximum recursion 에러
이 방법이 아닌가 싶었는데 10*5 2 의 값은 에러 없이 돌아갔다..

graph 의 값

[[], [2, 3, 4, 5], [1, 3, 4, 5], [1, 2, 4, 5], [1, 2, 3, 5], [1, 2, 3, 4]]
형태로, 자신을 제외한 모든 선으로 노드를 연결한다.

Visited

visited = [[0]*(N+1) for _ in range(N+1)]
1번 노드 -> 2번노드 , 2번 노드-> 1번노드 의 값은 다르기 때문에 2차원 배열로 생성한다.

Dfs(start_node)

while graph[start_node]:
  i = graph[start_node].pop(0)
  if visited[start_node][i] == 0: # 방문을 안했다 
    visited[start_node][i] = 1
    visited[i][start_node] = 1
    dfs(i)