[알고리즘] 프로그래머스 정수 삼각형 파이썬 | 다이나믹 프로그래밍

[프로그래머스] LEVEL3 정수 삼각형

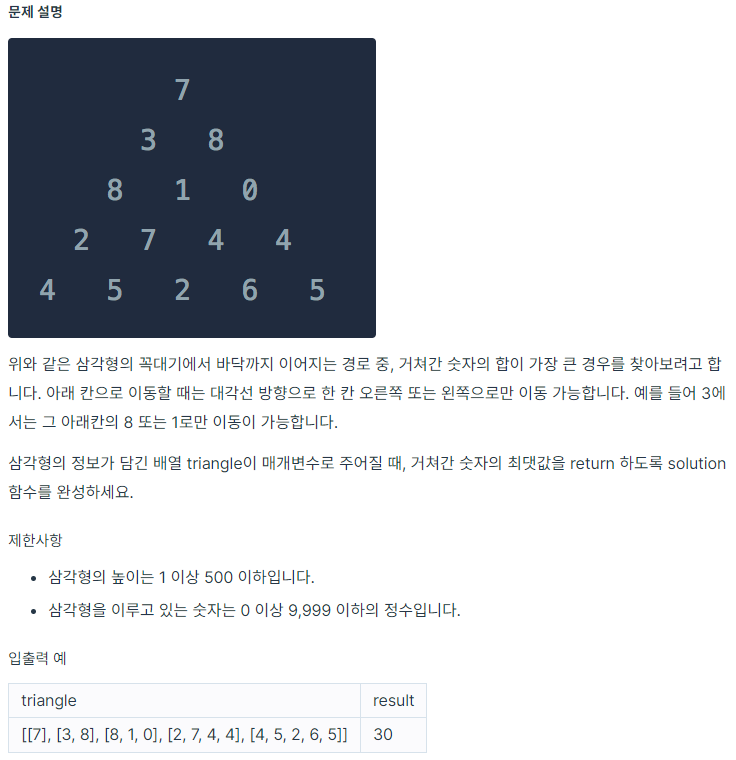
문제

나의 풀이

이번에 나 좀 잘한 것 같다 ㅎㅎ

def solution(t):
    for i in range(len(t)-1):
        tmp = 0
        for j in range(i+1):
            t[i+1][j] = max(t[i+1][j] + t[i][j], tmp)
            tmp = t[i+1][j+1] + t[i][j]
            if j == i:
                t[i+1][j+1] = tmp
    return max(t[-1])

다른 풀이

하지만 다른 풀이를 보니 tmp 변수는 불필요했다.

def solution(triangle):
    dp = []
    for t in range(1, len(triangle)):
        for i in range(t+1):
            if i == 0:
                triangle[t][0] += triangle[t-1][0]
            elif i == t:
                triangle[t][-1] += triangle[t-1][-1]
            else:
                triangle[t][i] += max(triangle[t-1][i-1], triangle[t-1][i])
    return max(triangle[-1])

내 풀이가 아래의 그림이라면 (위에서 아래 두 경우를 비교)

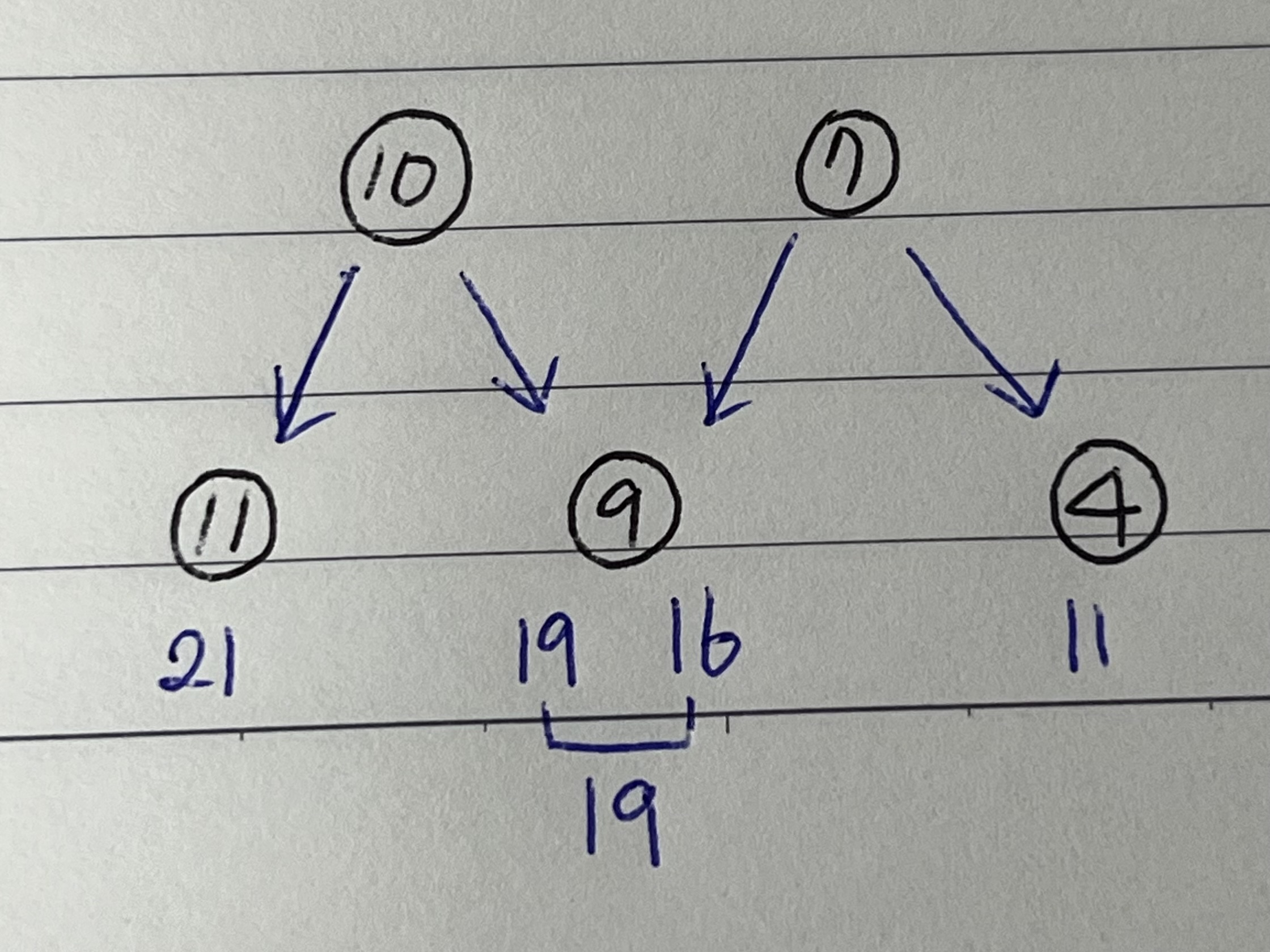
위 코드는 이 그림이다 (아래에서 위의 두 경우를 비교)

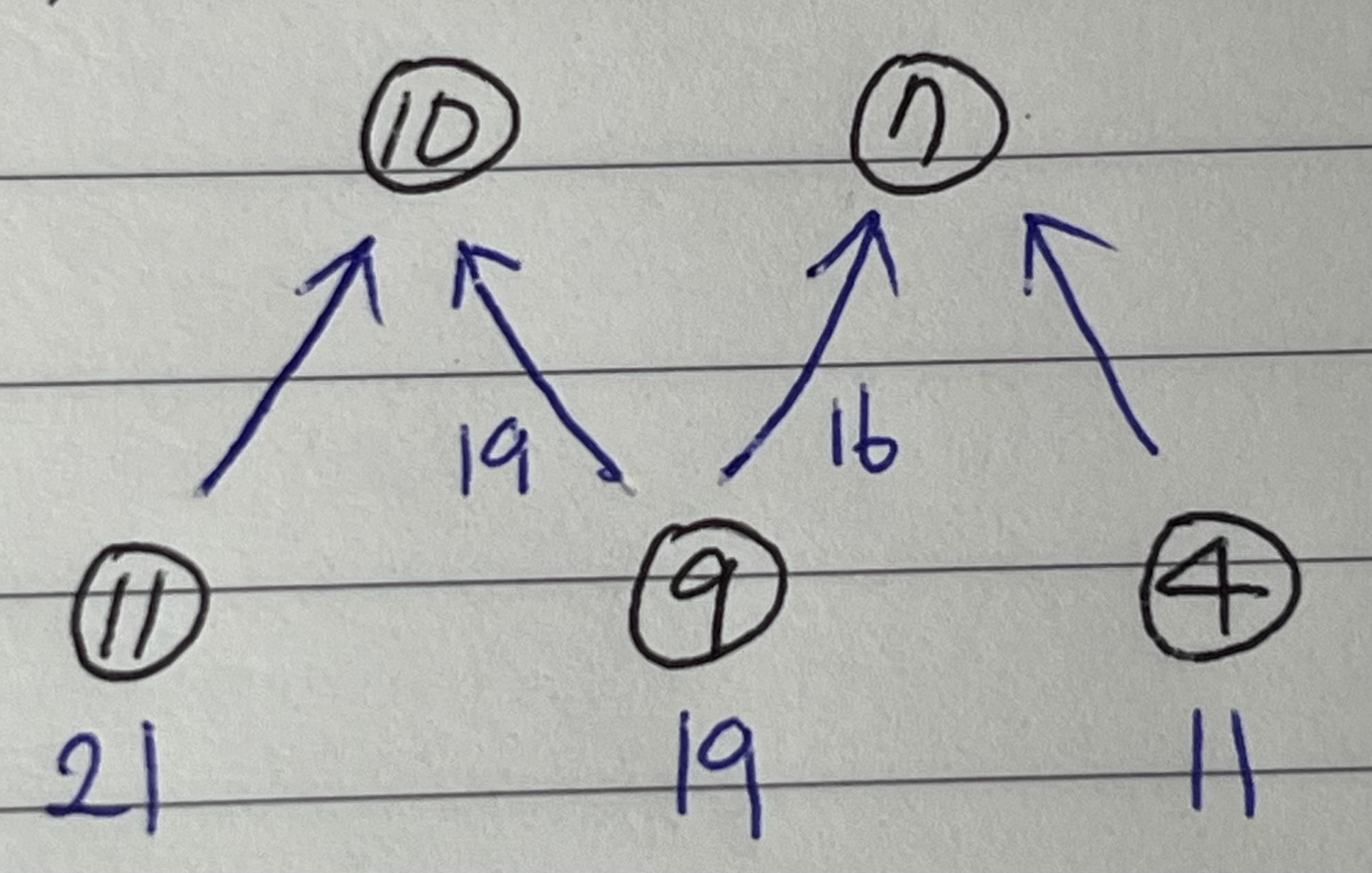
더욱 간단한 알고리즘이었다! 또 하나 배워간다.

얻어가기

생각 없이 구현했지만 이 알고리즘이 다이나믹 프로그래밍이었다. 배운 내용을 복습하자.

다이나믹 프로그래밍: 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법

이미 계산된 결과(작은 문제)는 별도의 메모리에 저장하여 다시 계산하지 않도록 한다. (한 번 해결한 문제는 다시 해결하지 않도록)

아래의 조건을 만족할 때 사용 가능하다.

1. 최적 부분 구조
   a. 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아 큰 문제 해결 가능
2. 중복되는 부분 문제
   a. 동일한 작은 문제를 반복적으로 해결

일반적으로 두 가지 방식, 탑다운과 바텀업으로 구성된다.

• 보통 탑다운은 재귀, 바텀업은 반복문 사용

• 탑다운 방식(햐향식), 메모이제이션(Memoization) : 한 번 계산한 결과를 메모리 공간에 메모하는 기법

  • 같은 문제를 다시 호출하면 메모 했던 결과를 그대로 가져옴
  • 값을 기록해 놓는다는 점에서 캐싱 caching이라고도 함

• 바텀업 방식(상향식)

  • 다이나믹 프로그래밍의 전형적인 형태
  • 결과 저장용 리스트는 DP 테이블이라고 부름