[알고리즘] 프로그래머스 이중우선순위큐 파이썬 | 힙

[프로그래머스] LEVEL3 이중우선순위큐

문제

나의 풀이

처음에는 힙 관련 모듈이 있음을 알지 못해 큐를 사용해 풀었다.
시간복잡도는 operations 길이를 N, 큐의 길이를 K라고 했을 때 최악의 경우 O(K^2N)이라고 생각한다.
하지만 정확하게는 모르겠다... 혹시 누군가 나의 글을 보신다면 피드백 환영...

from collections import deque

def solution(operations):
    queue = deque()
    
    for op in operations:
        if op[0] == 'I':
            num = int(op[2:])
            for i in range(len(queue)):
                if queue[i] > num:
                    queue.insert(i, num)
                    break
            else:
                queue.append(num)
        elif op == 'D 1':
            if len(queue) > 0:
                queue.pop()
        elif op == 'D -1':
            if len(queue) > 0:
                queue.popleft()
            
    if len(queue) == 0:
        return [0, 0]
    return [queue[-1], queue[0]]

다른 풀이

많은 사람들이 heapq를 이용해 문제를 풀었지만 여러 댓글을 보니 잘못된 풀이가 돌아다니고 있었다.
따라서 모든 조언들을 적용한 코드를 완성했다.
시간복잡도는 operations 길이를 N, 큐의 길이를 K라고 했을 때 O(KN)이라고 생각한다. 이 또한 피드백 환영.

from heapq import heappush, heappop, heapify

def solution(operations):
    min_heap = []
    max_heap = []
    
    for op in operations:
        if op[0] == 'I':
            num = int(op[2:])
            heappush(min_heap, num)
            heappush(max_heap, -num)
        elif op == 'D 1':
            if len(max_heap) > 0:
                min_heap.remove(-heappop(max_heap))
                heapify(min_heap)
        elif op == 'D -1':
            if len(min_heap) > 0:
                max_heap.remove(-heappop(min_heap))
                heapify(max_heap)
    if len(min_heap) == 0:
        return [0, 0]
    return [-heappop(max_heap), heappop(min_heap)]

remove() 함수 적용 시 heap의 구조가 깨지므로 heapify()로 재배치 해주어야 한다는 사실!
테스트 케이스 부족으로 연습 문제는 통과되지만 heapify()가 없다면 옳은 코드가 아니다.

얻어가기

Iterable.insert(index, value)

queue = deque(("p1", "p2", "p3", "p4"))
queue.insert(0, "p0")
print(queue)

# queue 길이보다 큰 index의 경우
queue.insert(10, "px")
print(queue)

# 0보다 작은 index의 경우
queue.insert(-9, "py")
print(queue)

deque(['p0', 'p1', 'p2', 'p3', 'p4'])
deque(['p0', 'p1', 'p2', 'p3', 'p4', 'px'])
deque(['py', 'p0', 'p1', 'p2', 'p3', 'p4', 'px'])

heapq

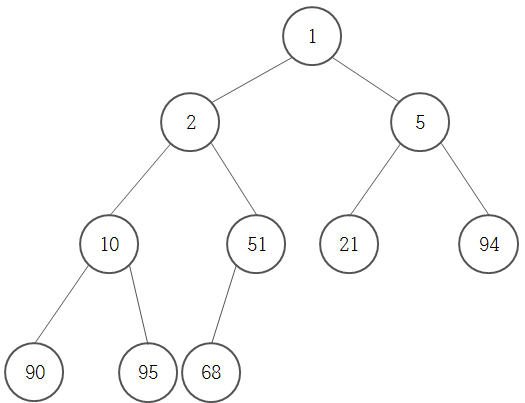
이 모듈은 우선순위 큐 알고리즘이라고도 하는 힙 큐 알고리즘의 구현을 제공한다. (min heap)

힙은 모든 부모 노드가 자식보다 작거나 같은 값을 갖는 이진 트리이다.

heappush(대상리스트, 원소) 힙의 성질에 따라 알맞은 위치에 삽입, O(logN)
heappop(대상리스트) 루트인 heap[0]를 pop, O(logN)
heapify(대상리스트) 기존 원소가 있는 리스트를 힙으로 재배치, O(N)
참고로 heap을 순서대로 나열했을 때 정렬된 상태가 아니다.

https://www.daleseo.com/python-heapq/