트리 순회 - 1991번
문제
이진 트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오.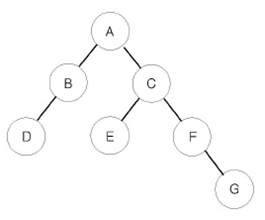 예를 들어 위와 같은 이진 트리가 입력되면,
예를 들어 위와 같은 이진 트리가 입력되면,
전위 순회한 결과 : ABDCEFG // (루트) (왼쪽 자식) (오른쪽 자식)
중위 순회한 결과 : DBAECFG // (왼쪽 자식) (루트) (오른쪽 자식)
후위 순회한 결과 : DBEGFCA // (왼쪽 자식) (오른쪽 자식) (루트)
가 된다.
입력
첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파벳 대문자로 매겨지며, 항상 A가 루트 노드가 된다. 자식 노드가 없는 경우에는 .으로 표현한다.
출력
첫째 줄에 전위 순회, 둘째 줄에 중위 순회, 셋째 줄에 후위 순회한 결과를 출력한다. 각 줄에 N개의 알파벳을 공백 없이 출력하면 된다.
풀이
어쨌든 실제로 코딩테스트를 볼 땐 매 문제마다 클래스 선언을 하지 않을 것 같으니, 클래스와 노드로 구현하는 쪽보단 기존에 계속해서 사용했던 리스트, 딕셔너리와 같은 파이썬 내장 자료구조로 구현하는 연습을 했다.
1. 트리를 딕셔너리로 만들어 풀이
다음의 코드는 정답이다.
def Tree():
import sys
input = sys.stdin.readline
N = int(input())
Fal = str(".")
tree = dict()
for _ in range(N):
root, leftnd, rightnd = input().split()
tree[root] = [leftnd, rightnd]
def Preorder(root):
if root!=Fal:
print(root, end='')
Preorder(tree[root][0])
Preorder(tree[root][1])
def Inorder(root):
if root!=Fal:
Inorder(tree[root][0])
print(root, end='')
Inorder(tree[root][1])
def Postorder(root):
if root!=Fal:
Postorder(tree[root][0])
Postorder(tree[root][1])
print(root, end='')
Preorder("A")
print(end="\n")
Inorder("A")
print(end="\n")
Postorder("A")
print(end="\n")
Tree()딕셔너리로 푸는 것은 상당히 간편했다.
위에서 처음에 변수 tree를 어케 만드느냐가 중요한 아이디어이다.
딕셔너리 변수 tree의 구성을 key와 value를 tree[root] = [leftnd, rightnd] 와 같이 만든다. 이는 결과적으로 다음과 같게 된다.
tree = {
‘A’ : {'B', 'C'},
‘B’ : ['D', '.'],
‘C’ : ['E', 'F'],
‘D’ : ['.', '.'],
‘E’ : ['.', '.'],
‘F’ : ['.', 'G'],
‘G’ : ['.', '.'],
}2-1. 파이썬에서 리스트로 트리
다음의 코드는 답안 제출과 상관 없이 공부를 위해 가져온 코드다.
def Tree():
TREE = ["A", ["B", ["D", [], [] ], [] ], ["C", ["E", [], [] ], ["F", [], ["G", [], [] ] ] ] ]
def Inorder(tree):
if tree:
Inorder(tree[1])
print(tree[0], end='')
Inorder(tree[2])
def Preorder(tree):
if tree:
print(tree[0], end='')
Preorder(tree[1])
Preorder(tree[2])
def Postorder(tree):
if tree:
Postorder(tree[1])
Postorder(tree[2])
print(tree[0], end='')
Preorder(TREE)
print(end="\n")
Inorder(TREE)
print(end="\n")
Postorder(TREE)
print(end="\n")
Tree()위 코드에서 tree는 다음과 같은 모습을 한다. 이진 트리의 구조를 생각하며 문제에 첨부된 그림과 같이 보면 금방 이해할 수 있다.
TREE = ["A",
["B",
["D",
[],
[]
],
[]
],
["C",
["E",
[],
[]
],
["F",
[],
["G",
[],
[]
]
]
]
]위가 기본적으로 파이썬의 리스트로 트리를 만드는 법이라고 한다. 영어로 서치하면 이와 같은 형식으로 접근하는 사람들이 아주 많다. https://stackoverflow.com/questions/61832670/traversing-a-binary-tree-using-a-list
그런데...
알고리즘 문제를 풀기 위해선 일정한 형식에 따른 입력값을 받아서 트리를 구현해야 하므로 이보다 "그래프의 한 종류로서의 트리"로 접근하는 것이 여러모로 옳다고 한다. (승훈이가 그랬음.) 자료구조 이론이란 재밌어~
graph 문제를 풀 땐 대강 이런 식으로 인풋 데이터를 담는다고 한다. 승훈이 문제 풀이 진도가 빨라서 나한테 이득이다 ㅋㅋ 늘 고마워용~
graph = [[] for _ in range(len(vertices) + 1)]
for i in range(len(edges)):
x, y = map(int, input().split())
graph[x].append(y)
graph[y].append(x) 2-2-1. 트리를 리스트로 만들어 풀이
다음의 코드는 정답이다.
N = int(input())
graph = [[] for _ in range(N+1)]
for i in range(1, N+1):
node,left,right = map(str, input().split())
graph[i].append(node)
graph[i].append(left)
graph[i].append(right)
Preorder = []
Inorder = []
Postorder = []
def tree(node):
Preorder.append(graph[node][0])
if graph[node][1] != '.':
for i in range(1, N+1):
if graph[i][0] == graph[node][1]:
tree(i)
Inorder.append(graph[node][0])
if graph[node][2] != '.':
for i in range(1, N+1):
if graph[i][0] == graph[node][2]:
tree(i)
Postorder.append(graph[node][0])
tree(1)
print(''.join(Preorder))
print(''.join(Inorder))
print(''.join(Postorder))변수 tree는 위 수행을 마치면 결과적으로 다음과 같게 된다.
graph = [
[],
['A', 'B', 'C'],
['B', 'D', '.'],
['C', 'E', 'F'],
['D', '.', '.'],
['E', '.', '.'],
['F', '.', 'G'],
['G', '.', '.'],
]Node의 번호는 1부터 시작하기 때문에 0은 비워두는 것이다.
현재 루트의 왼쪽 자식이 루트가 되게끔 한 칸 내려가는 함수, 오른쪽 자식이 루트가 되게끔 한 칸 내려가는 함수 이렇게 각각 떼왔다.
if graph[node][1] != '.':
for i in range(1, N+1):
if graph[i][0] == graph[node][1]:
Preorder(i) if graph[node][2] != '.':
for i in range(1, N+1):
if graph[i][0] == graph[node][2]:
Preorder(i)2-2-2. 트리를 리스트로 만들어 풀이
다음의 코드는 정답이다.
import sys
N = int(sys.stdin.readline())
tree = [list(map(str, sys.stdin.readline().split())) for _ in range(N)]
Fal = str(".")
def preorder(i):
root = tree[i][0]
left = tree[i][1]
right = tree[i][2]
print(root, end="")
if left!=Fal:
preorder(ord(left) - 65)
if right!=Fal:
preorder(ord(right) - 65)
def inorder(i):
root = tree[i][0]
left = tree[i][1]
right = tree[i][2]
if left!=Fal:
inorder(ord(left) - 65)
print(root, end="")
if right!=Fal:
inorder(ord(right) - 65)
def postorder(i):
root = tree[i][0]
left = tree[i][1]
right = tree[i][2]
if left!=Fal:
postorder(ord(left) - 65)
if right!=Fal:
postorder(ord(right) - 65)
print(root, end="")
preorder(0)
print(end="\n")
inorder(0)
print(end="\n")
postorder(0)동기 지희의 도움을 받았다.
일단 입력값을 받는 부분을 보자. 변수 tree는 위 수행을 마치면 결과적으로 다음과 같게 된다.
tree = [
['A', 'B', 'C'],
['B', 'D', '.'],
['C', 'E', 'F'],
['D', '.', '.'],
['E', '.', '.'],
['F', '.', 'G'],
['G', '.', '.'],
]아스키 코드의 A == 065, B == 066.... 이라는 점을 이용했다. 딕셔너리를 사용하지 않을 시 인자가 root의 값인 "B", "C" 등등 즉 스트링으로 넘어가서 어떻게 해야하나 어려웠는데, 영리한 풀이같다.