레드-블랙 트리(rbtree) 노드 삽입 연산에 대한 이해와 구현

조해빈·2023년 4월 11일
C자료구조
0

C

목록 보기
7/7

레드-블랙 트리의 삽입은 단순 이진 탐색 트리에서 하는 것과 동일하나, 새로 삽입되는 노드의 색은 무조건 붉은색인 것으로 시작한다.

삽입 연산을 들여다보기 전 rbtree의 속성 5가지를 정리하고 들어가자. 삽입 연산에서는 삽입으로 인한 속성이 깨지는 상황을 재조정한다. #3, #4, #5 의 속성들이 고려되어야 한다.

rbtree의 속성

  1. 모든 노드는 red or black.
  2. root = black.
  3. nil = black.
  4. red 노드 연속 불가.
  5. 어떤 노드에서 그 자손 nil 까지 가는 경로들은 그 경로의 과정 중에서 카운트할 수 있는 black의 수가 모두 동일하다.

아래의 아이디어는 경우의 가짓수에 따라 순번을 달 것이다. 이를 마치 거대한 하나의 수도코드(C언어)라고 생각해본 뒤, 아이디어를 코드 레벨로 발전시켜보자.

삽입 연산

기본적으로 삽입은 트리의 맨 끝(leaf)까지 내려가서 삽입된다. 말인즉 이진 탐색 트리의 기본 골격에 따라 옳은 자리를 찾을 때까지 하강하다가 더이상 내려갈 자식이 없는 단계에서 멈춘다.

이때,
💡 트리가 NULL이라면, 지금 삽입되는 노드가 트리의 가장 첫번째 노드이므로 이는 곧 루트 노드이다.

0. 부모의 노드 색깔을 확인

0-0. 삽입된 노드의 부모 색이 RED면, 삭제 시 위반 사항 없음.
삽입되는 노드의 부모가 black이라면, 연산이 종료된다.

0-1. 삽입된 노드의 부모 색이 BLACK이면, #4 속성 위반.
삽입되는 노드의 부모 색이 BLACK이면 속성 #4를 위반하게 되어 조치가 필요하다.

대강 여기까지의 수도코드가 아래와 같다.

0-1. 삽입되는 노드의 부모 색이 BLACK

삽입되는 노드의 부모 색이 BLACK이라면 삽입되는 노드의 삼촌(uncle), 즉 삽입되는 노드의 부모의 형제가 무슨 색인지를 확인해야 한다.

'삼촌 노드(uncle node)'라는 개념이 이제 도입되는데, 이는 같은 높이에 있는 옆 노드(다시 말해, 사촌)의 부모 노드(삼촌)를 뜻한다. 코드로 표현한다면 다음과 같다.

node uncle(node_t n)
{
    if (n->parent == grandparent(n)->left)
        return grandparent(n)->right;
    else
        return grandparent(n)->left;
}

동시에 '조부모 노드(grandparent node)' 역시 부모 노드의 부모 노드를 뜻한다.

node grandparent(node_t n)
{
    return n->parent->parent;
}

부모 노드와 삼촌 노드에 대한 연계의 경우의 수가 총 세가지가 있다. 이 경우에 따라 조정 과정이 달리한다.

case1. 삽입된 노드(red)의 부모도 red, 삼촌도 red
case2. 삼촌은 black이며, 삽입된 노드(red)가 부모의 오른쪽 자녀이며, 부모가 red
case3. 삼촌은 black이며, 삽입된 노드(red)가 부모의 왼쪽 자녀이며, 부모가 red

위 중 case2, case3은 각각 왼-오 반전일 경우도 당연히 같은 경우에 해당한다.

지금부터 삽입되는 노드를 z, z의 삼촌 노드를 y라고 칭해보자. 그렇다면 이 재조정에 대한 전체적인 수도코드는 다음과 같은 구조를 띌 수 있을 것이다.

while z.부모.색 == 빨강
	if z.부모 == z.부모.부모.왼쪽자식
    	if y.색 == 빨강
        	(case1)
        	.
            .
        else
        	if z == z.부모.오른쪽자식
            	(case2)
                .
            	.
            (case3)
            .
            .
    else
    (위 코드의 좌우반전 버전)
    .
    .

위를 바탕으로 이제 각 경우에 대한 연산을 따진다.

0-1-c1. yy가 red

Case1. 삽입된 노드(red)의 부모도 red, 삼촌도 red인 경우이다.

이땐 부모와 삼촌을 BLACK으로 바꾸고 할아버지를 RED로 바꾼다.
→ 현재의 Case 1이 Case 2로 바뀐다. 경우가 바뀌면서 z, y가 재설정된다. 이렇게 case를 변경하여 다시금 해결법을 도모할 수 있다.

0-1-c2. yy가 black, zz가 부모의 오른쪽 자녀

Case2. 삼촌은 black이며, 삽입된 노드(red)가 부모의 오른쪽 자녀이며, 부모가 red인 경우이다.

이땐 부모를 기준으로 왼쪽으로 회전한다. (왼쪽과 오른쪽을 바꾸면 반전된 경우에도 성립)
→ 현재의 Case 2이 Case 3으로 바뀐다. 경우가 바뀌면서 z, y가 재설정된다. 이렇게 case를 변경하여 다시금 해결법을 도모할 수 있다.

0-1-c3. yy가 black, zz가 부모의 왼쪽 자녀

Case3. 삼촌은 black이며, 삽입된 노드(red)가 부모의 왼쪽 자녀이며, 부모가 red인 경우이다.

이땐 부모와 할아버지의 색을 바꾼 후 할아버지 기준으로 오른쪽으로 회전한다.
(왼쪽과 오른쪽을 바꾸면 반전된 경우에도 성립)

오른쪽으로 회전하면 트리가 균형을 맞추고 모든 속성을 만족한다. 이로써 삽입 연산이 모두 종료된다.

위 3가지의 내용을 전반적으로 도식화하면 다음과 같다.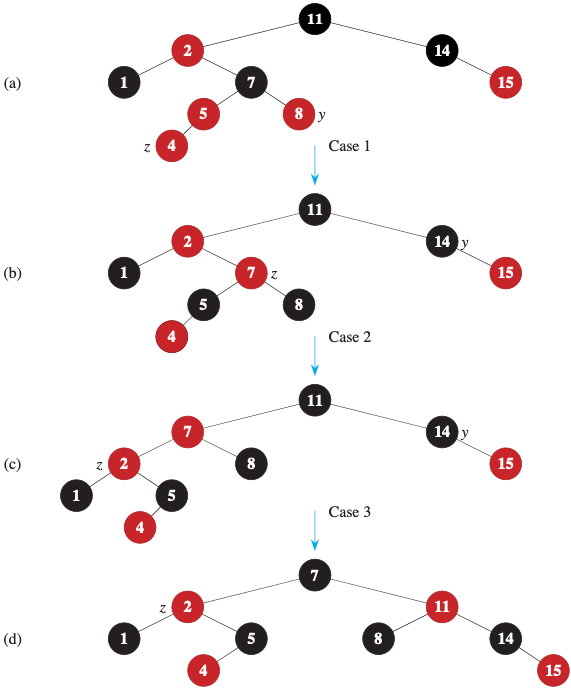
여기까지의 수도코드는 다음과 같다.

구현 코드

위를 참고하며 아래의 코드를 이해할 수 있다.
아래는 rbtree의 노드에 대한 삽입, 삭제 연산을 하는 코드이다.

#include "rbtree.h"
#include <stdio.h>
#include <stdlib.h>

rbtree *new_rbtree(void) {
  rbtree *p = (rbtree *)calloc(1, sizeof(rbtree));
  node_t *nilNode = (node_t *)calloc(1, sizeof(node_t));

  nilNode->color = RBTREE_BLACK;
  p->nil = nilNode;
  p->root = nilNode;

  return p;
}

void right_rotate(rbtree *t, node_t *y) {
  node_t *x; 

  x = y->left;                 // y애 대하여 right rotate를 수행했을 때 y의 자리에 들어올 노드(y의 left) 
  y->left = x->right;          // rotate 되면서 x의 right child가 y가 되므로, 기존에 있던 x의 right는 y의 left로 붙음

  if (x->right != t->nil)  {         // x의 right가 nil이 아니면 
    x->right->parent = y;            // x의 right의 parent를 y로 지정
  }
  x->parent = y->parent;              // rotate되어 y의 자리에 x가 들어오므로 x의 parent에 y의 parent를 넣어줌

  if (y->parent == t->nil)              // y가 root일 떄
    t->root = x;                        
  else if (y == y->parent->left) {              // y가 left child
    y->parent->left = x;   
  }
  else {                                        // y가 right child
    y->parent->right = x;
  }

  x->right = y;                                 //rotate를 마치고 x의 right를 y로
  y->parent = x;                                // y의 parent를 x로 바꿈
}

void left_rotate(rbtree *t, node_t *y) {
  node_t *x;

  x = y->right;               // rotate한 자리에 들어올 x 지정 (y의 right)
  y->right = x->left;         // rotate 되면서 x의 left chid가 y가 되므로, 기존에 있던 x의 left는 y의 right로 붙음

  if (x->left != t->nil) {           // x의 left가 nil이 아니면
    x->left->parent = y;             // parent를 y로 지정
  }
  x->parent = y->parent;             // rotate되어 y의 자리에 x가 들어오므로 x의 parent에 y의 parent를 넣어줌

  if (y->parent == t->nil) {            // y가 root일 때
    t->root = x;
  }
  else if (y == y->parent->left) {      // y가 left child
    y->parent->left = x;
  }
  else {                                // y가 right child
    y->parent->right=x;
  }
  x->left = y;                          // rotate를 마치고 x의 left를 y로
  y->parent = x;                        // y의 parent를 x로 바꿈

}

void free_node(rbtree *t, node_t *x) {       // 후위 순회 방식으로 노드와 하위 노드들의 메모리를 반환하는 함수
  if (x->left != t->nil)
    free_node(t, x->left);
  if (x->right != t->nil)
    free_node(t, x->right);

  free(x);
  x = NULL;                                  // 반환 후 포인터를 NULL로 초기화
}

void delete_rbtree(rbtree *t) {             // RB 트리의 메모리를 반환하는 함수
  if (t->root != t->nil)
    free_node(t, t->root);
  free(t->nil);
  free(t);
}

void rbtree_insert_fixup(rbtree *t, node_t *z) {      // RB 트리에 노드를 삽입하고 RB properties를 위반했을 때 해결하는 함수      
  node_t *y; 

  while (z->parent->color == RBTREE_RED){
    if (z->parent == z->parent->parent->left) {         // parent of z == left subtree
      y = z->parent->parent->right;                     // y : uncle
      if (y->color == RBTREE_RED) {                    // Case 1 : uncle.color == RED, parent.color == RED      
        z->parent->color = RBTREE_BLACK;               // parent, uncle의 color는 black으로, grandparent는 red로
        y->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        z = z->parent->parent;                        // z를 위로 옮겨주고 다시 parent가 red인지 확인
      }
      else {                                         //  Case 2 : uncle.color == BLACK
        if (z == z->parent->right) {                 // 꺾여있음 -> LEFT ROTATE 하여 Case 3으로 만들어 줌
        z = z->parent;
        left_rotate(t, z);       
        }                                            // Case 3 : parent = red, left child, uncle.color = BLACK
        z->parent->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        right_rotate(t, z->parent->parent);
      }
    }

    else {  // right & left exchanged (z->parent == z->parent->parent->left)
      y = z->parent->parent->left;
      if (y->color == RBTREE_RED) {  
        z->parent->color = RBTREE_BLACK;
        y->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        z = z->parent->parent;                           
      }
      else {
        if (z == z->parent->left) {                       
            z = z->parent;
            right_rotate(t, z);
          }
          z->parent->color = RBTREE_BLACK;
          z->parent->parent->color = RBTREE_RED;
          left_rotate(t, z->parent->parent);
          }
        }
      }
    t->root->color = RBTREE_BLACK;
}

node_t *rbtree_insert(rbtree *t, const key_t key) {

  node_t* x;
  node_t* y;
  node_t* z = (node_t*)calloc(1, sizeof(node_t));
  z->key = key;
  x = t->root;                  // node being compared with z
  y = t->nil;                   // y will be parent of z

  while (x != t->nil) {         // descend until reaching the sentinel
    y = x;
    if (z->key < x->key) {
      x = x->left;
    }
    else {
      x = x->right;
    }
  }

  z->parent = y;                 // found the location to be inserted -> insert z with parent y

  if(y == t->nil) {
    t->root = z;
  }
  else if (z->key < y->key) {
    y->left = z;
  }
  else {
    y->right = z;
  }
  z->left = t->nil;
  z->right = t->nil;
  z->color = RBTREE_RED;

  rbtree_insert_fixup(t, z);
  return t->root;
}


node_t *rbtree_find(const rbtree *t, const key_t key) {
  node_t *x;

  x = t->root;
  while (x != t->nil) {
    if (x->key == key) {
      return x;
    }
    else if (x->key < key) {
      x = x->right;
    }
    else if (x->key > key){
      x = x->left;
    }
  }
  return NULL;
}

node_t *rbtree_min(const rbtree *t) {
  node_t *x;
  if (t->root == t->nil)
    return NULL;
  x = t->root;
  while (x->left != t->nil) {
    x = x->left;
  }
  return x;
}

node_t *rbtree_max(const rbtree *t) {
  node_t *x;

  if (t->root == t->nil)
    return NULL;
  x = t->root;
  while (x->right != t->nil) {
    x = x->right;
  }
  return x;
}

void rbtree_transplant(rbtree *t, node_t *u, node_t *v){     
  if (u->parent == t->nil)       // 삭제되는 노드가 root 일 경우
    t->root = v;
  else if (u == u->parent->left) // 삭제되는 노드가 왼쪽 노드일 경우
    u->parent->left = v;
  else                           // 삭제되는 노드가 오른쪽 노드일 경우
    u->parent->right = v;
  v->parent = u->parent;
}

void rbtree_delete_fixup(rbtree *t, node_t *x) {
  while (x != t->root && x->color == RBTREE_BLACK){
    // case 1 ~ 4
    if (x == x->parent->left)  {              // is x a left child?
      node_t *w = x->parent->right;           // w : uncle

      if (w->color == RBTREE_RED){                   // case 1
        w->color = RBTREE_BLACK;
        x->parent->color = RBTREE_RED;
        left_rotate(t, x->parent);
        w = x->parent->right;
      }

      if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK){ // case 2
        w->color = RBTREE_RED;
        x = x->parent;
      }

      else{
        if (w->right->color == RBTREE_BLACK){  // case 3
          w->left->color = RBTREE_BLACK;
          w->color = RBTREE_RED;
          right_rotate(t, w);
          w = x->parent->right;
        }

        w->color = x->parent->color;              // case 4
        x->parent->color = RBTREE_BLACK;
        w->right->color = RBTREE_BLACK;
        left_rotate(t, x->parent);
        x = t->root;
        }
    }

    else {  // 반대 방향
      node_t *w = x->parent->left;

      if (w->color == RBTREE_RED){
        w->color = RBTREE_BLACK;
        x->parent->color = RBTREE_RED;
        right_rotate(t, x->parent);
        w = x->parent->left;
      }

      if (w->right->color == RBTREE_BLACK && w->left->color == RBTREE_BLACK) {
        w->color = RBTREE_RED;
        x = x->parent;
      }

      else
      {
        if (w->left->color == RBTREE_BLACK){
          w->right->color = RBTREE_BLACK;
          w->color = RBTREE_RED;
          left_rotate(t, w);
          w = x->parent->left;
        }
        w->color = x->parent->color;
        x->parent->color = RBTREE_BLACK;
        w->left->color = RBTREE_BLACK;
        right_rotate(t, x->parent);
        x = t->root;
      }
    }
  }
x->color = RBTREE_BLACK;
}

int rbtree_erase(rbtree *t, node_t *p) {
  node_t *y; 
  node_t *x;
  color_t y_original_color;

  y = p;
  y_original_color = y->color;
  if (p->left == t->nil) { // 삭제될 노드의 left가 nil이면 -> right를 그대로 가져옴
    x = p->right;
    rbtree_transplant(t, p, p->right);
  }
  else if (p->right == t->nil) {    // 삭제될 노드의 right가 nil -> left를 그대로 가져옴
    x = p->left;
    rbtree_transplant(t, p, p->left);
  }
  else {                // 노드 p의 left, right child가 모두 nil이 아닌 경우
    y = p->right;
    while(y->left != t->nil){
      y = y->left;                     // find successor y
      }
    y_original_color = y->color;
    x = y->right;   // successor의 오른쪽 자식
    if (y->parent == p){
      x->parent = y;
    }
    else {                                   // 삭제된 p의 위치에 들어올 successor가 멀리 떨어져 있음
      rbtree_transplant(t, y, y->right);     // 올라오기 전에 successor의 위치를 successor의 right로 대체
      y->right = p->right;                   // 삭제될 p의 right들을 y의 right에 붙여줌
      y->right->parent = y;                 //  y의 자녀들(p에서 옮겨진 자녀들)의 parent를 y로 수정
      }

    rbtree_transplant(t, p, y);            // p 를 successor y로 대체
    y->left = p->left;             // 삭제될 p의 left들을 y의 left에 붙여 줌
    y->left->parent = y;           // 붙인 p의 자녀들의 parent를 y로 수정     
    y->color = p->color;            // 삭제된 p의 color를 y가 가짐 
  }
  if (y_original_color == RBTREE_BLACK)   {  // 삭제된 자리를 채운 y의 원래 색깔이 BLACK일 경우
    rbtree_delete_fixup(t, x);
  }
  free(p);
  return 0; 
}


void inorderTraversal(const rbtree *t, node_t* x, int* arr, int* idx, const size_t n){
  if (x == t->nil)
      return;

    inorderTraversal(t, x->left, arr, idx, n);
    arr[*idx] = x->key;
    if (*idx == n-1)
      return;
    (*idx)++;
    inorderTraversal(t, x->right, arr, idx, n);
}

int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n) {
  int idx = 0;

  // array에 key 순서대로 삽입하기 위해 중위 순회를 진행 

  inorderTraversal(t, t->root, arr, &idx, n);
  return *arr;
}

아래의 자료들을 크게 참고했다.
https://ko.wikipedia.org/wiki/%EB%A0%88%EB%93%9C-%EB%B8%94%EB%9E%99_%ED%8A%B8%EB%A6%AC#%EC%82%BD%EC%9E%85(Insertion)
https://lemonlemon.tistory.com/135
https://ten-drawbridge-c07.notion.site/Red-Black-Tree-RB-Tree-6b86f3e926c8473cb5f61f88690c3796
https://www.youtube.com/watch?v=2MdsebfJOyM

profile
조해빈
JS, CSS, HTML, React etc
이전 포스트

레드-블랙 트리(rbtree) 노드 삭제 연산에 대한 이해와 구현

0개의 댓글