레드-블랙 트리(rbtree) 노드 삭제 연산에 대한 이해와 구현

조해빈·2023년 4월 5일

C

목록 보기

6/7

레드-블랙 트리 노드의 삭제 연산은 일반적인 이진 탐색 트리(BST)의 삭제 연산과 같다. 기본적으로 이진 탐색 트리에서 삭제를 수행할 때에는 왼쪽 서브트리에서의 최댓값이나, 오른쪽 서브트리에서의 최솟값을 삭제한 노드의 위치에 삽입한다. 다르게 말하면, successor가 대체된다. 삭제 후 rbtree 속성 5가지가 위반되었는지 확인하고 위반되었을 경우 이를 재조정하여 자동으로 트리의 균형을 맞춘다.

이 때 생각해볼 수 있는 점은, 삭제한 노드를 대체할 노드에는 반드시 1개의 자식 노드만 있다는 점이다. (그 이유는 즉슨, 대체할 노드가 자식 2개를 보유한 경우 그 값이 왼쪽 자식 < 대체 노드 < 오른쪽 자식이라는 결론이 도출되므로, 결과론적인 면에서 봤을 때 대체할 노드가 자식 2개를 보유하게 될 가능성은 절대적으로 0이기 때문이다.)

때문에, 모든 노드 삭제는 최대 한 개의 non-leaf 자식을 갖고 있는 노드를 삭제하는 경우로 좁혀서 생각할 수 있다. 최대 한 개의 non-leaf 자식을 가진 노드를 지우는 문제 뿐 아니라 두 개의 non-leaf 자식을 가진 노드를 지우는 문제까지도 적용할 수 있기 때문이다.

삭제 연산을 들여다보기 전 rbtree의 속성 5가지를 정리하고 들어가자.

rbtree의 속성

모든 노드는 red or black.

root = black.

nil = black.

red 노드 연속 불가.

어떤 노드에서 그 자손 nil 까지 가는 경로들은 그 경로의 과정 중에서 카운트할 수 있는 black의 수가 모두 동일하다.

아래의 아이디어는 경우의 가짓수에 따라 순번을 달 것이다. 이를 마치 거대한 하나의 수도코드(C언어)라고 생각해본 뒤, 아이디어를 코드 레벨로 발전시켜보자.

삭제 연산

0. ‘자식 보유 상태’와 ‘어떤 색이 삭제되는지’를 확인.

0-a. 삭제되는 노드가 오른쪽 자식(내부 노드)이 없다면, 왼쪽 자식이 삭제되는 노드의 자리에 이식된다.
0-b. 삭제되는 노드가 왼쪽 자식(내부 노드)이 없다면, 오른쪽 자식이 삭제되는 노드의 자리에 이식된다.
0-c. 삭제되는 노드의 자식이 둘이라면, 삭제되는 노드의 successor와 값을 교환한 뒤 successor가 삭제된다.

(여기서 자녀란 nil이 아닌, 유효한 값을 갖는 노드 즉 내부 노드만을 고려한다.)(successor란 어떤 노드의 오른쪽 서브트리 중 가장 값이 작은 노드, 혹은 왼쪽 서브트리 중 가장 값이 큰 노드를 말한다.)

이때, 우선 노드의 값만 그 자리로 옮긴다고 생각한다. 우선 값과 포인터들을 조작한 뒤, 색은 곧 재확인해 줄 것이다.

위 경우들을 조금 자세히 구상해본다.

삭제하고자 한 노드를 z라고 칭해본다. 우리는 코드 내에서 우선 0-a와 0-b의 경우 z의 색깔을, 0-c의 경우 z의 successor의 색깔을 따로 기록해둘 필요가 있다. 이 색은 삭제되는 색이다.

💡 삭제하려는 노드가 자녀(내부 노드)가 없거나 하나라면: 삭제되는 색은 삭제되는 노드의 색.
💡 삭제하려는 노드가 자녀(내부 노드)가 둘이라면: 삭제되는 색은 삭제되는 노드의 successor의 색.

후자가 0-c에 해당하겠다.

0-c을 좀 더 들여다본다. (통상적으로 successor를 오른쪽 서브트리 중 가장 값이 작은 노드로써 구한다. 이를 if문을 짜고 행여 오른쪽 서브트리가 없을 경우를 else문으로 방어한다고 생각한다.)

z의 successor를 y라고 칭해보자. z에 들어갈 y의 값을 배치하고 그의 오른쪽에 삭제된 z의 오른쪽 자식을 붙인다. z를 y로 이식한다. y의 왼쪽에 z의 왼쪽 자식을 붙인다. y의 색은 z의 색으로 대체된다.

이제 여기서 삭제되는 색에 대해 체크한다. 이 색은 아까 우리가 기록해뒀던 색이다.

0-0. 삭제되는 색이 RED면, 삭제 시 위반 사항 없음.
삭제되는 노드가 red라면 해당 노드 삭제 수행.

0-1.삭제되는 노드가 BLACK면, #2, #4, #5 위반 가능.
삭제되는 노드가 black이라면 rbtree의 속성이 깨졌을 확률이 높다(특히 #5). 이땐 깨진 속성들을 하나하나 맞춰준다.

0-1-0. 속성 #2 위반 시.

삭제되는 노드가 black이며 그때 그 삭제된 노드가 그 트리의 루트였을 경우, 속성 #2가 깨진다.

이땐 루트 노드를 black으로 바꿔준다.

이렇게 rbtree의 모든 속성이 모두 재충족된다.

0-1-1. 속성 #5 위반 시.

속성 #4를 위반했음은 곧 속성 #5를 위반한 경우에 포함된다. 사실상 매우 특수한 경우가 아니고서는 black 노드를 삭제할 시 속성 #5를 위반하게 된다.

이땐 삭제된 색의 위치에 자리하게 된 노드에게 "extra black"을 부여한다.

속성 #5를 재충족시키기 위해 이뤄지는 연산이라고 생각한다면 이해가 쉽다. 적절한 비유인지 모르겠지만, 마치 카드게임 중 테이블 위 카드를 못 수거하고 두 장 겹쳐놓게 된 상태라 생각해보자...

💡 삭제된 색의 위치에 자리하게 된 노드는 black일 수도, red일 수도, nil일 수도 있다.

0-1-1-0. extra black 상태가 된 노드가 red였다면, 이는 "red-and-black" 상태가 칭한다.

0-1-1-1. extra black 상태가 된 노드가 black이었다면 이는 "doubly black", 즉 "이중 흑색노드"라 칭한다.

extra black은 트리 내에서 궁극적으로 해소되어야하는 개념이다. 이제부터 다양한 경우에 따른 이 extra black을 해갈하는 방법론에 대해 나열해본다.

0-1-1-0. "red-and-black" 발생 시.

이땐 red였던 해당 노드를 단순히 black으로 바꿔준다.

이렇게 rbtree의 모든 속성이 모두 재충족된다.

0-1-1-1. "doubly black" 발생 시.

doubly black은 해소되어야하는 개념이라고 했다. doubly black이 발생하는 경우는 총 4가지로 귀결된다. 각각 doubly black의 형제와, 그 형제의 자식들의 색에 따라 갈리는 것이다.

4가지에 대해선 아래와 같이 도식화할 수 있다.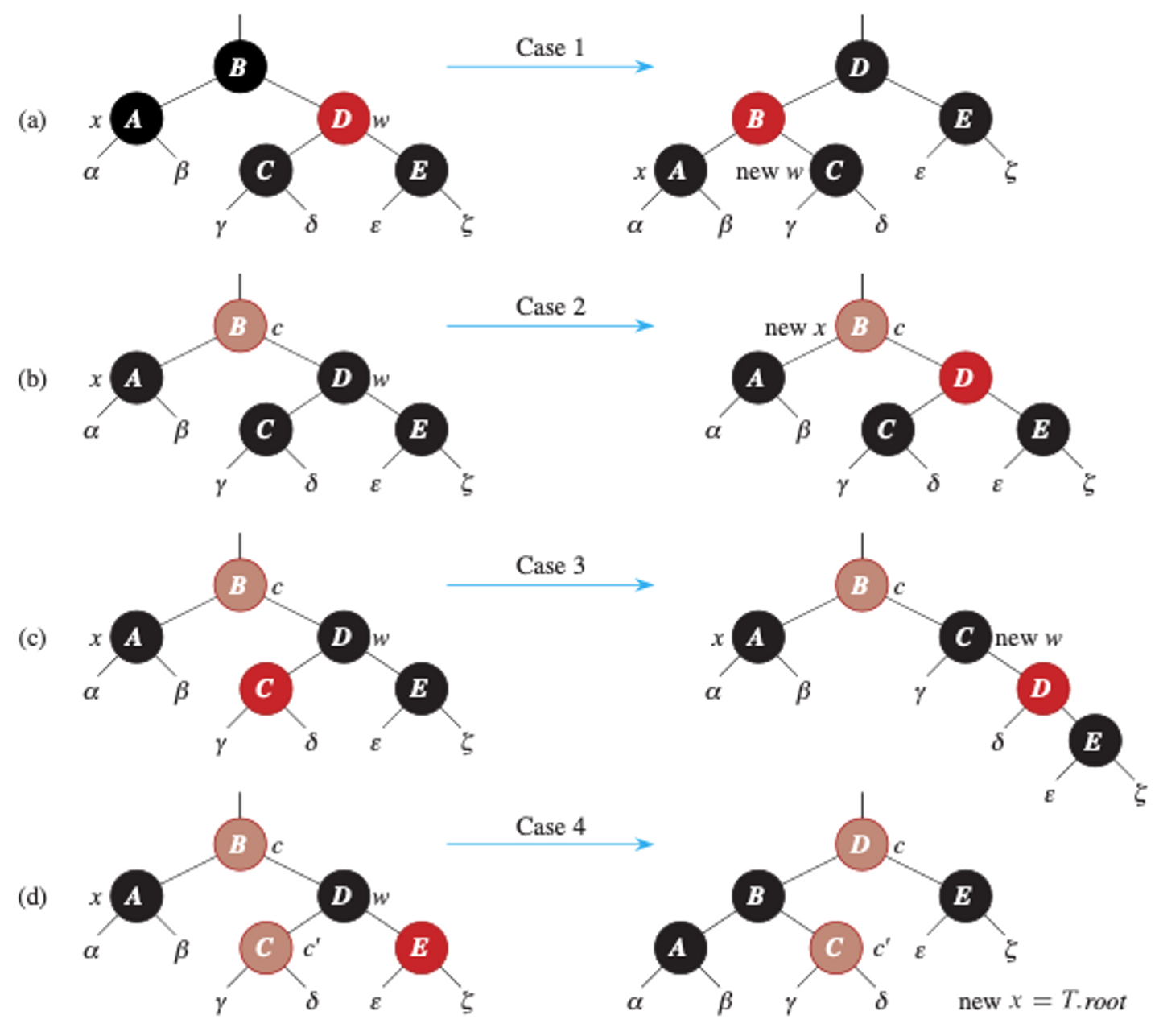
이제부터 이중흑색노드 즉 doubly black인 노드를 x라고 칭해보자.

0-1-1-1-c1. $x$ ’s sibling $w$ is red.

Case1. 이중흑색노드 $x$ 의 형제 $w$ 가 RED 인 경우이다.

이땐 형제를 검은색, 부모를 빨간색으로 칠한다. 그리고 부모노드를 기준으로 좌회전 한다.

다르게 말해 red 노드를 doubly black 노드의 직속 상위 위치로 이동시켜주기 위함이라 생각해볼 수 있다.

여기서 잠시 생각해볼 때, 속성 #4로 인해 $x$ 와 $w$ 의 부모는 무조건 black이다. 고로 '형제를 검은색, 부모를 빨간색으로 칠한다'함은 곧 부모와 color를 바꾸는 개념과 동일하다.

부모와 color를 바꾸고 left-rotate한다.
→ left-rotate로 인해 $x$ 의 sibling이 c로 바뀐다 (new $w$ ).
→ 현재의 Case 1이 Case 2, 3, or 4로 바뀐다. 경우가 바뀌면서 $w$ 가 재설정된다. 이렇게 case를 변경하여 다시금 해결법을 도모할 수 있다.

0-1-1-1-c2. $x$ ’s sibling $w$ and both of $w$ ’s children are black.

Case2. 이중흑색노드 $x$ 의 형제 $w$ 가 BLACK 이고 $w$ 의 양쪽 자식 모두 BLACK 인 경우이다.

이땐 $w$ 의 자녀들이 모두 black이므로, $w$ 의 black과 doubly black $x$ 의 black을 부모 노드로 올려준다.

이 시점에서 우린 extra black 두 개가 모이면 그것을 부모에게 하나의 extra black으로서 올려보낼 수 있다는 점을 활용한다. 쉽게 말해 형제노드만 RED 로 만들고, $x$ 와 $w$ 의 부모를 new $x$ 로 재설정하여 다시금 해결법을 도모할 수 있다.

여기서 부모가 red였다면 이제 부모는 red-and-black이 될 것이다. 이 경우 부모가 그냥 black이 되면서 모든 연산이 종료된다!

여기서 부모가 black이다면 이제 부모는 doubly-black이 될 것이다. 이 경우 현재의 Case 2가 Case 1, 2, 3, or 4로 바뀐다. 경우가 바뀌면서 이 부모 노드는 new $w$ , 즉 새로운 케이스의 $w$ 로 재설정된다. 이렇게 case를 변경하여 다시금 해결법을 도모할 수 있다.

0-1-1-1-c3. $x$ ’s sibling $w$ is black, $w$ ’s left child is red, and $w$ ’s right child is black.

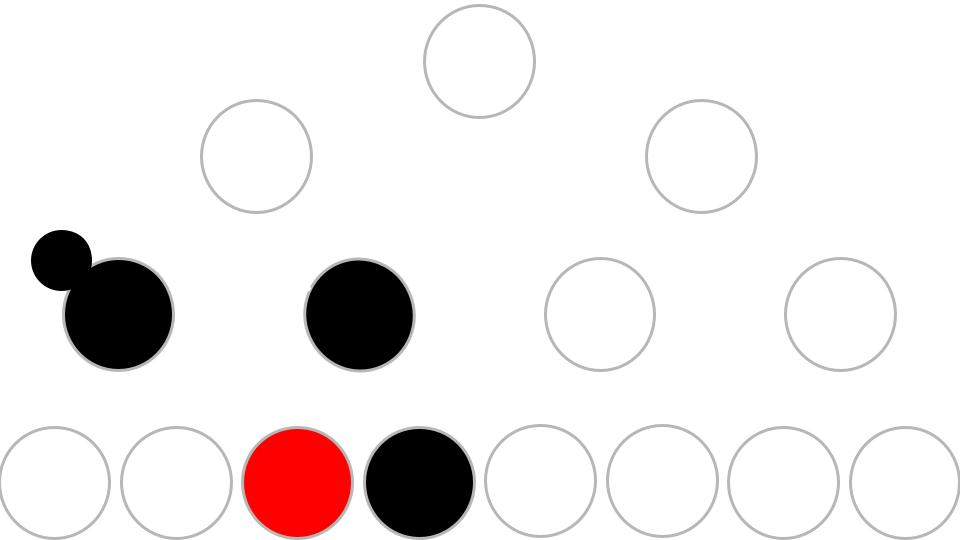Case3. 이중흑색노드 $x$ 의 형제 $w$ 가 BLACK 이고 $w$ 의 왼쪽 자식이 RED, 오른쪽 자식이 BLACK 인 경우이다. (사람에 따라 case 3을 그냥 형제 $w$ 가 BLACK 이고 $w$ 의 왼쪽 자식이 RED인 경우로 정의하기도 하는 것 같다.)

이땐 형제노드를 RED 로, 형제노드의 왼쪽 자식을 BLACK 으로 칠한 후에 형제 노드를 기준으로 우회전 한다.

이는 생각해보면 결국 $w$ 와 $w$ 의 왼쪽 자식을 색 교환한 뒤, $w$ 의 오른쪽 자식이 red가 되게끔 만들어 해결에 접근하는 것이다.

부모와 color를 바꾸고 right-rotate한다.
→ right-rotate로 인해 $x$ 의 sibling이 c로 바뀐다 (new $w$ ).
→ 현재의 Case 3이 Case 4로 바뀐다. 경우가 바뀌면서 $w$ 가 재설정된다. 이렇게 case를 변경하여 다시금 해결법을 도모할 수 있다.

0-1-1-1-c4. $x$ ’s sibling $w$ is black, and $w$ ’s right child is red.

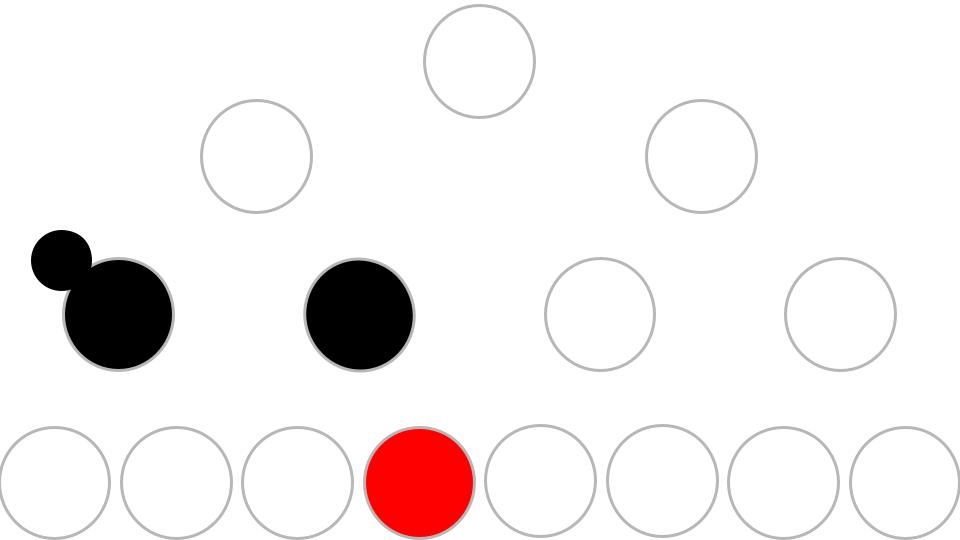Case4. 이중흑색노드 $x$ 의 형제 $w$ 가 BLACK 이고 $w$ 의 오른쪽 자식이 RED 인 경우이다.

이땐 부모 노드의 색을 형제에게 넘긴 뒤, 부모노드와 형제노드의 오른쪽 자식을 검은색으로 칠한다. 그리고 부모 노드 기준으로 좌회전 한다.

이는 다시 말해 red를 doubly black의 위로 옮기고, 옮긴 red로 extra black을 전달하여 red-and-black으로 만드는 것이다.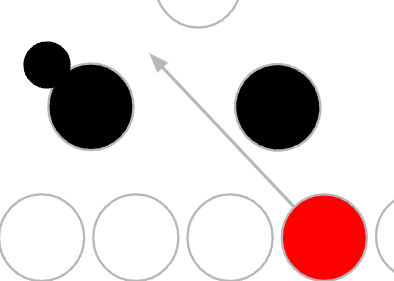

red를 왼쪽으로 보내기 위해서는 D의 위치가 red가 되어야 하고,
→ 이를 위해 D의 black을 아래 C, E로 내려 주고, D가 red가 된다.
→ D를 left-rotate하기 전, 부모 B와 색을 바꿔준다. (B가 red가 되고, D가 brown이 된다.)
→ 왼쪽으로 넘어간 red B는 자식들의 extra black을 2개 (A(doubly black), C(extra black)) 전이받아 black이 된다.
→ extra black이 해결되면서 모든 연산이 종료된다!

이로써 삭제 연산이 모두 종료된다.

📍 삭제 연산에 대한 전체적인 수도코드

z = 삭제되는 노드

0. ‘자식 보유 상태’와 ‘어떤 색이 삭제되는지’를 확인.

0-0. z의 색이 RED: 삭제 시 위반 사항 없음.
0-1. z의 색이 BLACK: #2, #4, #5 위반 가능.

0-1-0. z가 루트(속성 #2 위반): → 루트 노드를 black으로 바꿔준다.
0-1-1. z의 서브트리 균형 어그러짐(속성 #5 위반): → 삭제된 색의 위치에 자리하게 된 노드에게 "extra black"을 부여한다.

x = extra black 상태가 된 노드

0-1-1-0. x가 red: "red-and-black" → red였던 해당 노드를 단순히 black으로 바꿔준다.
0-1-1-1. x가 black: "doubly black" → 아래의 경우에 맞춰 extra black을 해소한다.

0-1-1-1-c1. x의 형제가 RED
→ 부모와 color를 바꾸고 left-rotate한다.
→ left-rotate로 인해 x의 sibling이 c로 바뀐다 (new w).
→→Case 2, 3, or 4로 바뀐다.

0-1-1-1-c2. x의 형제 BLACK, x의 형제의 양쪽 자식 BLACK
if... 여기서 부모가 red: 이제 부모는 red-and-black이 될 것이다. →→→ 부모가 black이 되면서 연산 종료.
if... 여기서 부모가 black: 이제 부모는 doubly-black이 될 것이다. →→Case 1, 2, 3, or 4로 바뀐다.

0-1-1-1-c3. x의 형제 BLACK, x의 형제의 좌측 자식 RED, x의 형제의 우측 자식 BLACK
→ 부모와 color를 바꾸고 right-rotate한다.
→ right-rotate로 인해 x의 sibling이 c로 바뀐다 (new w).
→→Case 4로 바뀐다.

0-1-1-1-c4. x의 형제 BLACK, x의 형제의 우측 자식 RED
→ 부모 노드의 색을 형제에게 넘긴 뒤, 부모노드와 형제노드의 오른쪽 자식을 검은색으로 칠한다. 그리고 부모 노드 기준으로 좌회전 한다. →→→ 부모가 black이 되면서 연산 종료.

구현 코드

위를 참고하며 아래의 코드를 이해할 수 있다.
아래는 rbtree의 노드에 대한 삽입, 삭제 연산을 하는 코드이다.

#include "rbtree.h"
#include <stdio.h>
#include <stdlib.h>

rbtree *new_rbtree(void) {
  rbtree *p = (rbtree *)calloc(1, sizeof(rbtree));
  node_t *nilNode = (node_t *)calloc(1, sizeof(node_t));

  nilNode->color = RBTREE_BLACK;
  p->nil = nilNode;
  p->root = nilNode;

  return p;
}

void right_rotate(rbtree *t, node_t *y) {
  node_t *x; 

  x = y->left;                 // y애 대하여 right rotate를 수행했을 때 y의 자리에 들어올 노드(y의 left) 
  y->left = x->right;          // rotate 되면서 x의 right child가 y가 되므로, 기존에 있던 x의 right는 y의 left로 붙음

  if (x->right != t->nil)  {         // x의 right가 nil이 아니면 
    x->right->parent = y;            // x의 right의 parent를 y로 지정
  }
  x->parent = y->parent;              // rotate되어 y의 자리에 x가 들어오므로 x의 parent에 y의 parent를 넣어줌

  if (y->parent == t->nil)              // y가 root일 떄
    t->root = x;                        
  else if (y == y->parent->left) {              // y가 left child
    y->parent->left = x;   
  }
  else {                                        // y가 right child
    y->parent->right = x;
  }

  x->right = y;                                 //rotate를 마치고 x의 right를 y로
  y->parent = x;                                // y의 parent를 x로 바꿈
}

void left_rotate(rbtree *t, node_t *y) {
  node_t *x;

  x = y->right;               // rotate한 자리에 들어올 x 지정 (y의 right)
  y->right = x->left;         // rotate 되면서 x의 left chid가 y가 되므로, 기존에 있던 x의 left는 y의 right로 붙음

  if (x->left != t->nil) {           // x의 left가 nil이 아니면
    x->left->parent = y;             // parent를 y로 지정
  }
  x->parent = y->parent;             // rotate되어 y의 자리에 x가 들어오므로 x의 parent에 y의 parent를 넣어줌

  if (y->parent == t->nil) {            // y가 root일 때
    t->root = x;
  }
  else if (y == y->parent->left) {      // y가 left child
    y->parent->left = x;
  }
  else {                                // y가 right child
    y->parent->right=x;
  }
  x->left = y;                          // rotate를 마치고 x의 left를 y로
  y->parent = x;                        // y의 parent를 x로 바꿈

}

void free_node(rbtree *t, node_t *x) {       // 후위 순회 방식으로 노드와 하위 노드들의 메모리를 반환하는 함수
  if (x->left != t->nil)
    free_node(t, x->left);
  if (x->right != t->nil)
    free_node(t, x->right);

  free(x);
  x = NULL;                                  // 반환 후 포인터를 NULL로 초기화
}

void delete_rbtree(rbtree *t) {             // RB 트리의 메모리를 반환하는 함수
  if (t->root != t->nil)
    free_node(t, t->root);
  free(t->nil);
  free(t);
}

void rbtree_insert_fixup(rbtree *t, node_t *z) {      // RB 트리에 노드를 삽입하고 RB properties를 위반했을 때 해결하는 함수      
  node_t *y; 

  while (z->parent->color == RBTREE_RED){
    if (z->parent == z->parent->parent->left) {         // parent of z == left subtree
      y = z->parent->parent->right;                     // y : uncle
      if (y->color == RBTREE_RED) {                    // Case 1 : uncle.color == RED, parent.color == RED      
        z->parent->color = RBTREE_BLACK;               // parent, uncle의 color는 black으로, grandparent는 red로
        y->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        z = z->parent->parent;                        // z를 위로 옮겨주고 다시 parent가 red인지 확인
      }
      else {                                         //  Case 2 : uncle.color == BLACK
        if (z == z->parent->right) {                 // 꺾여있음 -> LEFT ROTATE 하여 Case 3으로 만들어 줌
        z = z->parent;
        left_rotate(t, z);       
        }                                            // Case 3 : parent = red, left child, uncle.color = BLACK
        z->parent->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        right_rotate(t, z->parent->parent);
      }
    }

    else {  // right & left exchanged (z->parent == z->parent->parent->left)
      y = z->parent->parent->left;
      if (y->color == RBTREE_RED) {  
        z->parent->color = RBTREE_BLACK;
        y->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        z = z->parent->parent;                           
      }
      else {
        if (z == z->parent->left) {                       
            z = z->parent;
            right_rotate(t, z);
          }
          z->parent->color = RBTREE_BLACK;
          z->parent->parent->color = RBTREE_RED;
          left_rotate(t, z->parent->parent);
          }
        }
      }
    t->root->color = RBTREE_BLACK;
}

node_t *rbtree_insert(rbtree *t, const key_t key) {

  node_t* x;
  node_t* y;
  node_t* z = (node_t*)calloc(1, sizeof(node_t));
  z->key = key;
  x = t->root;                  // node being compared with z
  y = t->nil;                   // y will be parent of z

  while (x != t->nil) {         // descend until reaching the sentinel
    y = x;
    if (z->key < x->key) {
      x = x->left;
    }
    else {
      x = x->right;
    }
  }

  z->parent = y;                 // found the location to be inserted -> insert z with parent y

  if(y == t->nil) {
    t->root = z;
  }
  else if (z->key < y->key) {
    y->left = z;
  }
  else {
    y->right = z;
  }
  z->left = t->nil;
  z->right = t->nil;
  z->color = RBTREE_RED;

  rbtree_insert_fixup(t, z);
  return t->root;
}


node_t *rbtree_find(const rbtree *t, const key_t key) {
  node_t *x;

  x = t->root;
  while (x != t->nil) {
    if (x->key == key) {
      return x;
    }
    else if (x->key < key) {
      x = x->right;
    }
    else if (x->key > key){
      x = x->left;
    }
  }
  return NULL;
}

node_t *rbtree_min(const rbtree *t) {
  node_t *x;
  if (t->root == t->nil)
    return NULL;
  x = t->root;
  while (x->left != t->nil) {
    x = x->left;
  }
  return x;
}

node_t *rbtree_max(const rbtree *t) {
  node_t *x;

  if (t->root == t->nil)
    return NULL;
  x = t->root;
  while (x->right != t->nil) {
    x = x->right;
  }
  return x;
}

void rbtree_transplant(rbtree *t, node_t *u, node_t *v){     
  if (u->parent == t->nil)       // 삭제되는 노드가 root 일 경우
    t->root = v;
  else if (u == u->parent->left) // 삭제되는 노드가 왼쪽 노드일 경우
    u->parent->left = v;
  else                           // 삭제되는 노드가 오른쪽 노드일 경우
    u->parent->right = v;
  v->parent = u->parent;
}

void rbtree_delete_fixup(rbtree *t, node_t *x) {
  while (x != t->root && x->color == RBTREE_BLACK){
    // case 1 ~ 4
    if (x == x->parent->left)  {              // is x a left child?
      node_t *w = x->parent->right;           // w : uncle

      if (w->color == RBTREE_RED){                   // case 1
        w->color = RBTREE_BLACK;
        x->parent->color = RBTREE_RED;
        left_rotate(t, x->parent);
        w = x->parent->right;
      }

      if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK){ // case 2
        w->color = RBTREE_RED;
        x = x->parent;
      }

      else{
        if (w->right->color == RBTREE_BLACK){  // case 3
          w->left->color = RBTREE_BLACK;
          w->color = RBTREE_RED;
          right_rotate(t, w);
          w = x->parent->right;
        }

        w->color = x->parent->color;              // case 4
        x->parent->color = RBTREE_BLACK;
        w->right->color = RBTREE_BLACK;
        left_rotate(t, x->parent);
        x = t->root;
        }
    }

    else {  // 반대 방향
      node_t *w = x->parent->left;

      if (w->color == RBTREE_RED){
        w->color = RBTREE_BLACK;
        x->parent->color = RBTREE_RED;
        right_rotate(t, x->parent);
        w = x->parent->left;
      }

      if (w->right->color == RBTREE_BLACK && w->left->color == RBTREE_BLACK) {
        w->color = RBTREE_RED;
        x = x->parent;
      }

      else
      {
        if (w->left->color == RBTREE_BLACK){
          w->right->color = RBTREE_BLACK;
          w->color = RBTREE_RED;
          left_rotate(t, w);
          w = x->parent->left;
        }
        w->color = x->parent->color;
        x->parent->color = RBTREE_BLACK;
        w->left->color = RBTREE_BLACK;
        right_rotate(t, x->parent);
        x = t->root;
      }
    }
  }
x->color = RBTREE_BLACK;
}

int rbtree_erase(rbtree *t, node_t *p) {
  node_t *y; 
  node_t *x;
  color_t y_original_color;

  y = p;
  y_original_color = y->color;
  if (p->left == t->nil) { // 삭제될 노드의 left가 nil이면 -> right를 그대로 가져옴
    x = p->right;
    rbtree_transplant(t, p, p->right);
  }
  else if (p->right == t->nil) {    // 삭제될 노드의 right가 nil -> left를 그대로 가져옴
    x = p->left;
    rbtree_transplant(t, p, p->left);
  }
  else {                // 노드 p의 left, right child가 모두 nil이 아닌 경우
    y = p->right;
    while(y->left != t->nil){
      y = y->left;                     // find successor y
      }
    y_original_color = y->color;
    x = y->right;   // successor의 오른쪽 자식
    if (y->parent == p){
      x->parent = y;
    }
    else {                                   // 삭제된 p의 위치에 들어올 successor가 멀리 떨어져 있음
      rbtree_transplant(t, y, y->right);     // 올라오기 전에 successor의 위치를 successor의 right로 대체
      y->right = p->right;                   // 삭제될 p의 right들을 y의 right에 붙여줌
      y->right->parent = y;                 //  y의 자녀들(p에서 옮겨진 자녀들)의 parent를 y로 수정
      }

    rbtree_transplant(t, p, y);            // p 를 successor y로 대체
    y->left = p->left;             // 삭제될 p의 left들을 y의 left에 붙여 줌
    y->left->parent = y;           // 붙인 p의 자녀들의 parent를 y로 수정     
    y->color = p->color;            // 삭제된 p의 color를 y가 가짐 
  }
  if (y_original_color == RBTREE_BLACK)   {  // 삭제된 자리를 채운 y의 원래 색깔이 BLACK일 경우
    rbtree_delete_fixup(t, x);
  }
  free(p);
  return 0; 
}


void inorderTraversal(const rbtree *t, node_t* x, int* arr, int* idx, const size_t n){
  if (x == t->nil)
      return;

    inorderTraversal(t, x->left, arr, idx, n);
    arr[*idx] = x->key;
    if (*idx == n-1)
      return;
    (*idx)++;
    inorderTraversal(t, x->right, arr, idx, n);
}

int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n) {
  int idx = 0;

  // array에 key 순서대로 삽입하기 위해 중위 순회를 진행 

  inorderTraversal(t, t->root, arr, &idx, n);
  return *arr;
}

아래의 자료들을 크게 참고했다.
https://ko.wikipedia.org/wiki/%EB%A0%88%EB%93%9C-%EB%B8%94%EB%9E%99_%ED%8A%B8%EB%A6%AC#%EC%82%AD%EC%A0%9C(Removal)
https://www.youtube.com/watch?v=6drLl777k-E
https://velog.io/@metamong/%EB%A0%88%EB%93%9C-%EB%B8%94%EB%9E%99-%ED%8A%B8%EB%A6%ACRed-Black-Tree
https://woonys.tistory.com/entry/%EC%A0%95%EA%B8%80%EC%82%AC%EA%B4%80%ED%95%99%EA%B5%90-37%EC%9D%BC%EC%B0%A8-TIL-Red-Black-TreeRB%ED%8A%B8%EB%A6%AC-%EC%82%AD%EC%A0%9C-%EA%B5%AC%ED%98%84

조해빈

JS, CSS, HTML, React etc

이전 포스트

쓰는중 자료구조 구현 - C를 통한 연결리스트의 구현

다음 포스트

레드-블랙 트리(rbtree) 노드 삭제 연산에 대한 이해와 구현

C

rbtree의 속성

삭제 연산

0. ‘자식 보유 상태’와 ‘어떤 색이 삭제되는지’를 확인.

0-1-0. 속성 #2 위반 시.

0-1-1. 속성 #5 위반 시.

0-1-1-0. "red-and-black" 발생 시.

0-1-1-1. "doubly black" 발생 시.

0-1-1-1-c1. $x$ ’s sibling $w$ is red.

0-1-1-1-c2. $x$ ’s sibling $w$ and both of $w$ ’s children are black.

0-1-1-1-c3. $x$ ’s sibling $w$ is black, $w$ ’s left child is red, and $w$ ’s right child is black.

0-1-1-1-c4. $x$ ’s sibling $w$ is black, and $w$ ’s right child is red.

📍 삭제 연산에 대한 전체적인 수도코드

구현 코드

쓰는중 자료구조 구현 - C를 통한 연결리스트의 구현

레드-블랙 트리(rbtree) 노드 삽입 연산에 대한 이해와 구현

0개의 댓글

레드-블랙 트리(rbtree) 노드 삭제 연산에 대한 이해와 구현

C

rbtree의 속성

삭제 연산

0. ‘자식 보유 상태’와 ‘어떤 색이 삭제되는지’를 확인.

0-1-0. 속성 #2 위반 시.

0-1-1. 속성 #5 위반 시.

0-1-1-0. "red-and-black" 발생 시.

0-1-1-1. "doubly black" 발생 시.

0-1-1-1-c1. xxx’s sibling www is red.

0-1-1-1-c2. xxx’s sibling www and both of www’s children are black.

0-1-1-1-c3. xxx’s sibling www is black, www’s left child is red, and www’s right child is black.

0-1-1-1-c4. xxx’s sibling www is black, and www’s right child is red.

📍 삭제 연산에 대한 전체적인 수도코드

구현 코드

쓰는중 자료구조 구현 - C를 통한 연결리스트의 구현

레드-블랙 트리(rbtree) 노드 삽입 연산에 대한 이해와 구현

0개의 댓글

0-1-1-1-c1. $x$ ’s sibling $w$ is red.

0-1-1-1-c2. $x$ ’s sibling $w$ and both of $w$ ’s children are black.

0-1-1-1-c3. $x$ ’s sibling $w$ is black, $w$ ’s left child is red, and $w$ ’s right child is black.

0-1-1-1-c4. $x$ ’s sibling $w$ is black, and $w$ ’s right child is red.