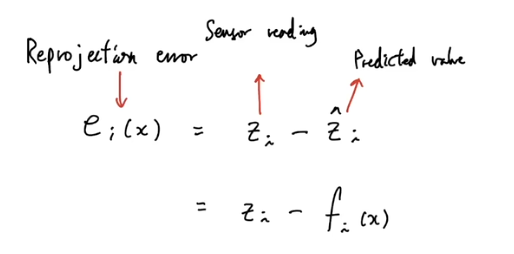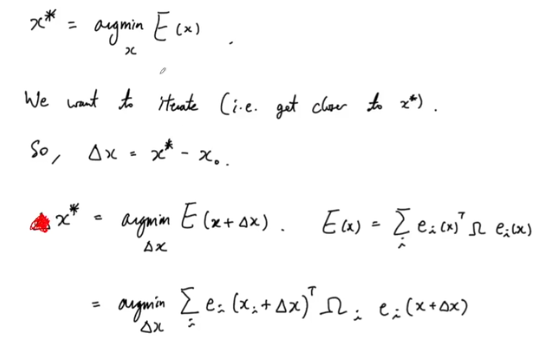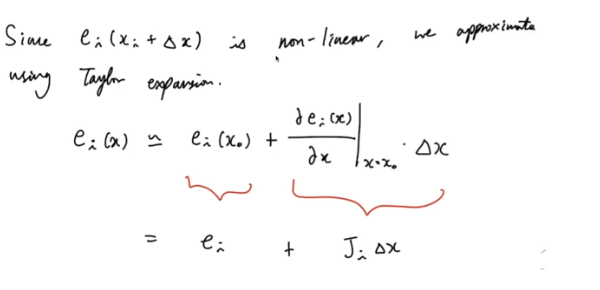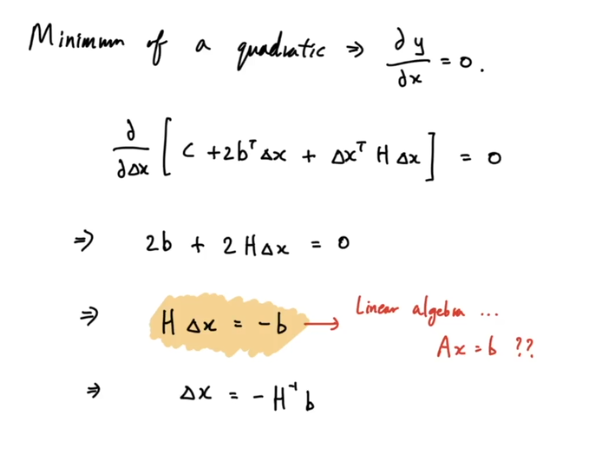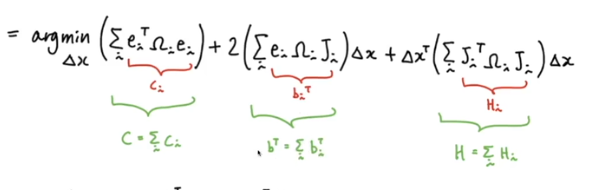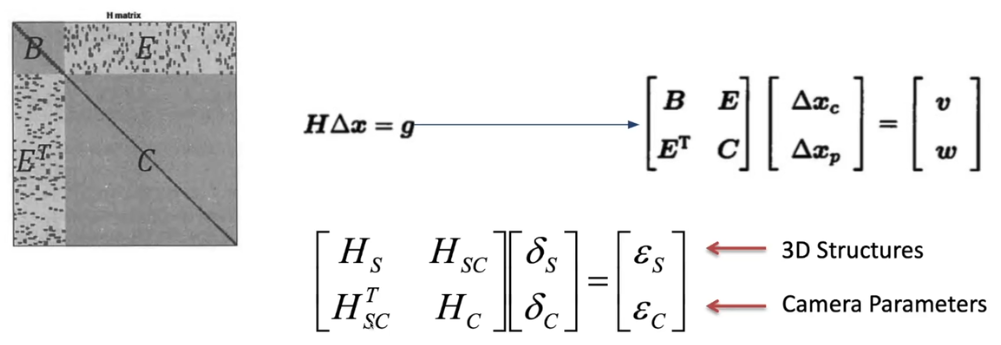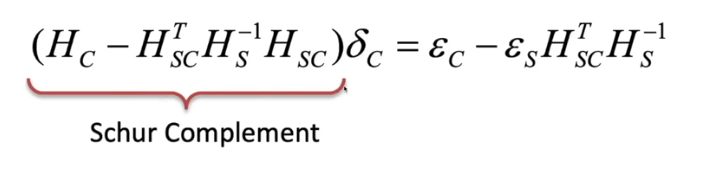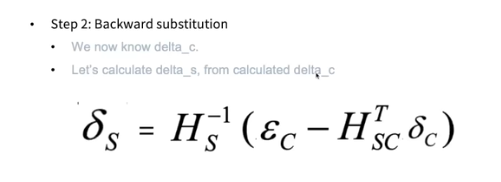[SLAM] 19. Bundle Adjustment

1. Bundle Adjustment

N-view geometry

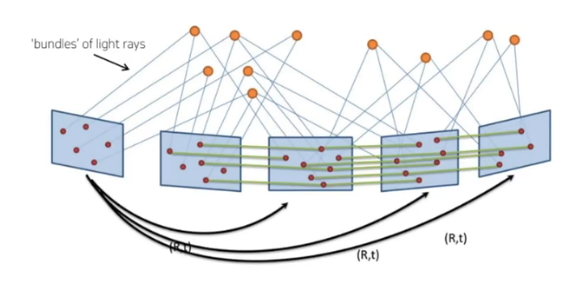
• 여러개의 프레임이 있고 각각의 프레임마다 relative motion 즉, rotation과 translation 값을 가지고 있다
• 2D-2D correspondence 공유하고 있다
• landmark들의 3D location도 알고 있다
• 하나의 landmark에 2개 이상의 2D-3D correspondence로 있다

• 로봇이 이동하면서 프레임마다 motion과 observation noise가 프레임마다 쌓인다
• 다 서로 매칭되어 있어도 실제로 정확한 값은 아닐 수 있다
• 이 uncertainty를 해결하기 위해 batch SLAM 기법을 적용한다
• 2D-2D correspondence, 2D-3D correspondence, relative motion 값을 이용해서 카메라 pose와 landmark position을 고정해준다 -> 이게 bundle adjustment의 목적

cost function

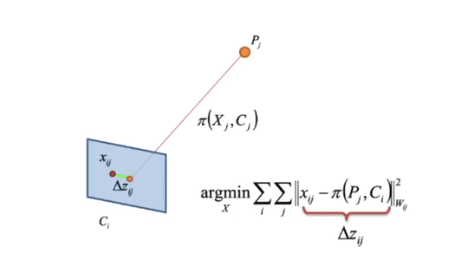
• 보정 = 그래프 최적화를 통해 uncertainty를 해소해준다
• reprojection error
  • 추정한 3D landmark의 position이 정확하고 카메라의 pose로 정확하다면 3D landmark를 이미지에 투영했을 때 정확하게 keypoint feature 위치랑 같을 것이다
  • 하지만 노이즈가 있기 때문에 오차가 생긴다
  • 이 오차를 픽셀 단위로 표현한 것 = reprojection error
• 이 오차를 해결하기 위해서
  • 1. landmark가 keypoint로 이동하는가
  • 2. 카메라가 ray로 가까이 가는가

nonlinear optimization

• 최적화 = total reprojection error가 최소화되는 최적의 카메라 pose와 lanemark position을 찾는 것
• 하지만 image projection 과정이 linear하지 않기 때문에 기본적인 최적화 수식을 사용할 때 error와 파라미터 space에서 단순 미분으로 최적화를 진행할 수 없다
• 따라서 비선형 최적화 방법을 사용한다

• 비선형 error 파라미터 space = error manifold
• 어떻게 비선형 공간에서 선형 공간으로 근사화 시켜서 iteratively하게 최적의 값으로 이동하는지 알아본다
• gussian-newton method

SLAM에서 bundle adjustment(BA)의 사용

• loop closure
  • factor graph에서 loop가 발생 -> 누적된 error를 BA를 통해 해소시켜줄 수 있다
• sliding-window optimization
  • 최근 n개의 keyframe을 가지고 BA를 돌려서 최적화를 하여 실시간으로 좋은 pose를 추론하는 방법

---

2. Nonlinear optimization

Gauss-Newton Method

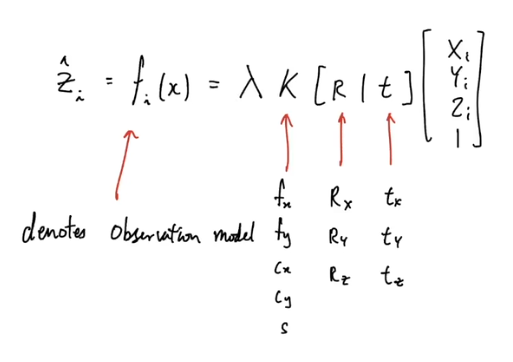
• BA에서 사용하는 observation 식
• 3D landmark position (X, Y, Z, 1)
• camera의 rotation R과 translantion t
• intrinsic K (fx, fy, cx, cy, s) -> 단일 카메라의 경우 고정되기 때문에 5개는 계산에서 제외된다 하지만 BA의 경우 여러 카메라를 사용하기 때문에 바뀔 수 있다

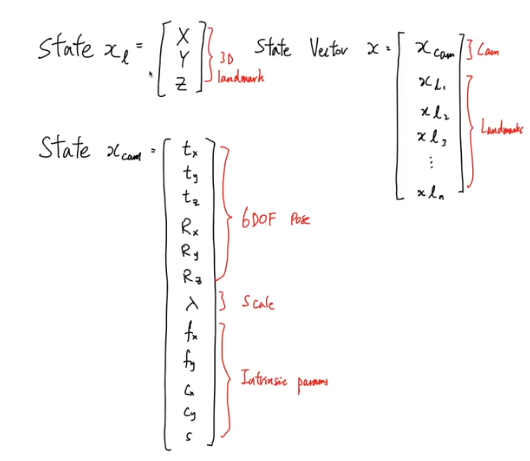
• state vector로 표현
• xl : landmark에 대한 state
• xcam : camera에 대한 state
• state vector : slam state

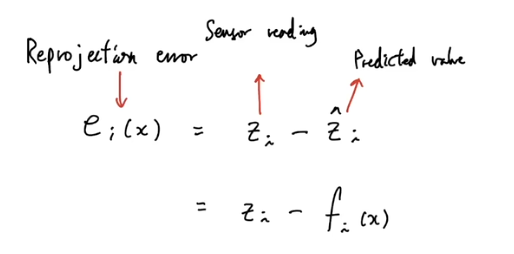
• BA 최적화 문제는 total projection error를 최소화하는 state vector는 어떤 값을 가지는가
• 이를 풀기 위해 least square 최적화를 수행하는데 이떄 noise는 가우시간 분포를 이루고 있다고 전제
• 왜 가우시안?
  • 실제 센서의 노이즈를 보면 가우시안이 아닌 경우도 있다
  • least square 최적화 문제는 노이즈가 가우시안 분포인 노이즈를 사용하게 되면 Maximum Likelihood Estimation (MLE) 문제로 수렴
  • MLE 문제는 정답을 구했을 때 정답이 통계적으로 최적의 값을 가진다는 것이 보장
  • 간단하다

• least square 최적화 식에 가우시안 적용
• $\omega$ : covariance matrix = information matrix

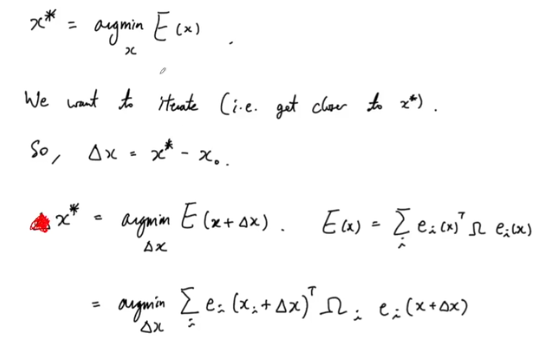
• x* : 최적의 값
• argmin E(x) : 위의 가우시안을 적용한 식
• x에서 x* 로 옮기고 싶다
• $\delta x$ : x* 와 x의 차이 / 이를 기존에 식에 적용
• $\delta x$로 식을 변환

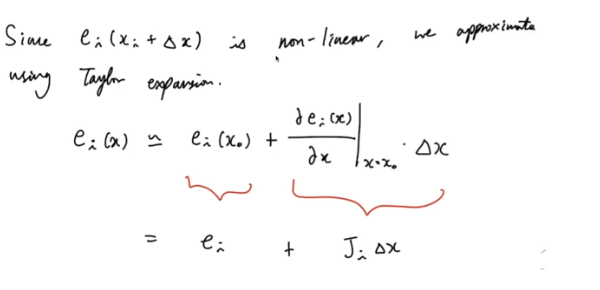
• 비선형하기 때문에 미분을 통해 선형으로 바꿔준다
• J : matrix의 1차 미분값

• 1차 미분값을 원래 식에 적용
• 최종 2차 방정식

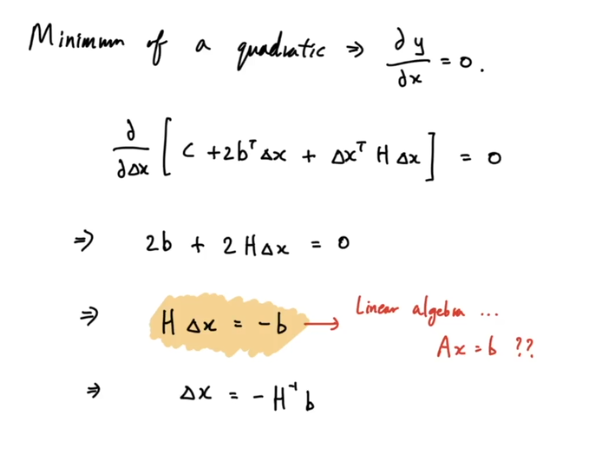
• 2차 방적식의 특징
• 미분을 해서 0이면 최대값, 최소값이 나온다
• 여기서는 항상 최소값이 나온다

• 의미를 살펴보면
• x0에서 시작해서 이때의 미분값을 구하고 이 1차 미분값과 근사하는 2차 방정식이 나온다.
• 이 방정식의 최소값을 구하면 -> local minimum -> 정답에 가까워진것이지 global optima라고 생각하지 않음
• 여기서 델타x는 x1과 x0의 이동치를 구한것
• 그럼 x0에 텔타 x를 더해서 x1로 이동
• 이 과정 반복
• x1에서 1차 미분해서 2차 방정식을 구하고 이것의 minimum을 구하고 x1에서 x2의 이동치를 구함
• 이를 반복하면 점점 정답에 가까워진다 = iterative solving

• 하지만 x = -H{-1}b 를 푸는 것이 어렵다
• H matrix가 굉장히 크기 때문이다
• BA를 풀때 보면 Jacobian matrix가 크고 이를 inverse하는 것은 엄청 오래걸린다

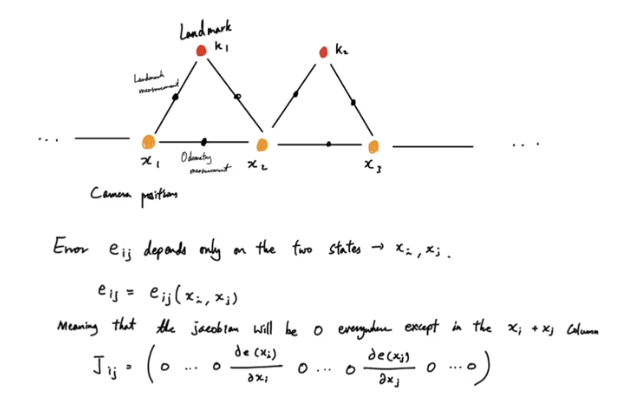
• 그래서 이 J matrix의 특성을 이용해본다
• J matrix
  • 대부분의 element가 비어 있다 (sparsity)
  • factor들마다 연결성을 미분한 matrix인데 node들은 인접한 것끼리 연결되어 있지만 멀리 떨어진 것들끼리는 연결이 잘 안되어 있다 -> 거의 대부분의 node끼리 연결되어 있지 않다 -> element 값이 0이다

• b matrix 역시 비어있다
• information과 error가 dense matrix라고 해도 J가 거의 비어 있기 때문에 b도 거의 비어있다

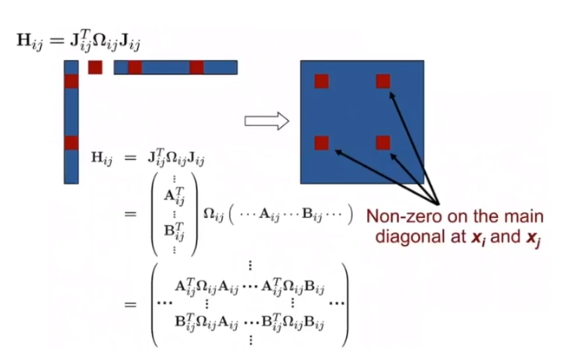
• 같은 이유도 H 도 거의 비어있다 + Symmetric 하다(대칭)

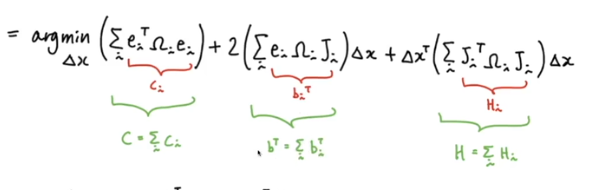
• 원래 식을 보면 b 하나하나를 더해서 하나의 큰 b matrix가 되고 H도 하나의 큰 matrix가 된다

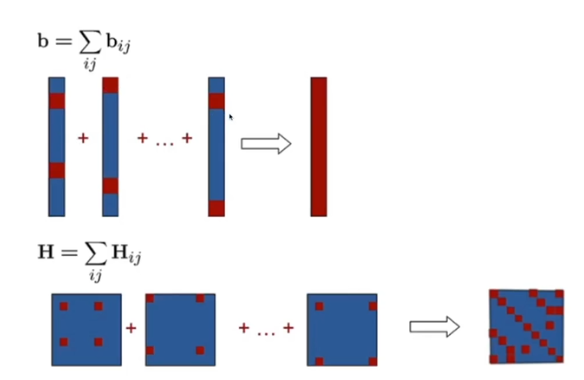
• total b matrix를 만드는 것은 sparse b matrix를 다 더하고 나서 dense한 matrix가 된다
• H도 다 합쳐서 만들지만 조금 sparse하다. 하지만 Symmetric 하다.

• H가 sparse 하다는 것을 알았으니 sparse matrix의 inverse 방법을 사용해서 빠르게 H의 inverse를 구할 수 있다
• 계속 반복하면 optimal한 파라미터를 구할 수 있다.
• 하지만 sparse한 matrix를 사용하는 것이 좋은 방법은 아니다

schur complement

• 더 좋은 방법

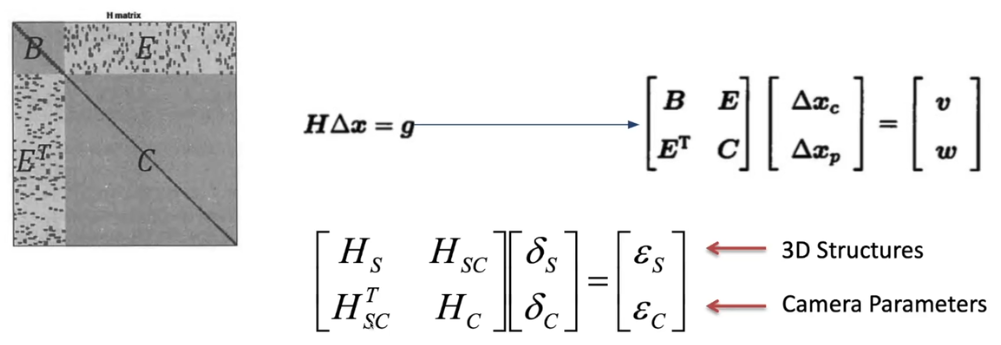
• H matrix는 이런 구조로 되어 있다
• S (B는 옛날표기): 3D structure , (x,y,z) location에 대한 정보
• C : camera pose에 관한 정보
• camera pose는 로봇이 이동할 때마다 생기는 것, 파라미터 수가 많다(rx,ry,rz,tx,ty,tz)
• B : landmark는 동일한 point, (x,y,z)
• 그래서 C가 B보다 크다
• SC : structure와 camera 간의 관계 -> obsevation에 관한 식

• 델타c로 계산을 할 수 있게 된다

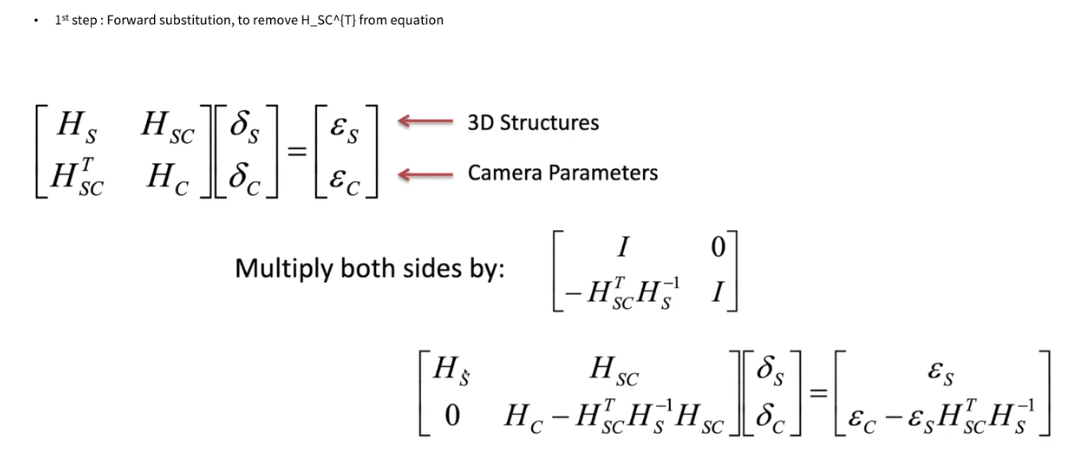
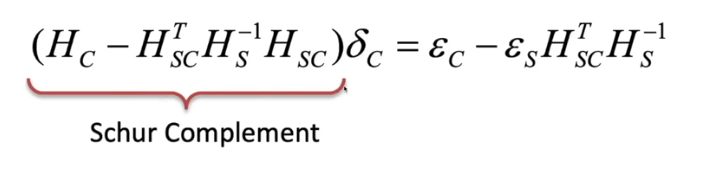
• 델타c로 표현한 식을 schur complement 식라고 한다
• 이미 다 알고 있고 Hs의 inverse만 구하면 된다 -> 이거 구하는 거는 쉽다
• Hs가 3x3 matrix여서 빠르다

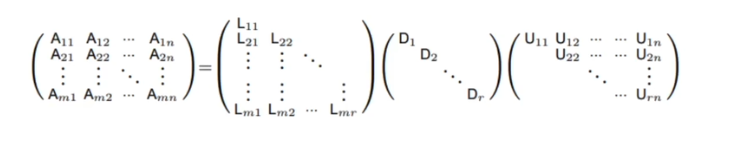
• 하지만 아직 inverse하기에는 크다
• 왼쪽 matrix를 다 합쳐서 크게 만들고 나중에 분해해서 계산한다

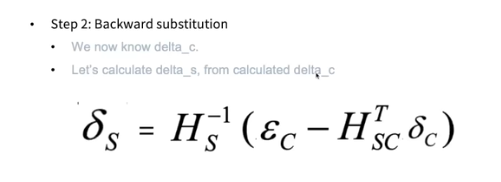
• 방금 델타 c를 구했으니까 델타s를 구하면 된다
• 델타c : 카메라 파라미터를 어떻게 정해야 델타 s랑 같아지나
• 델타 s는 landmark을 어떻게 정해야하는지에 대한 것

outlier rejection

m-estimator

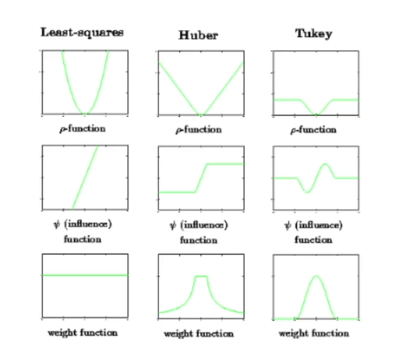
• least square non-linear할 때 조심해야할 점
• outlier에 취약한 알고리즘 중 하나이다
• m-estimator 커널 등을 사용하여 데이터 속에서 분포를 벗어나는 outlier를 최적화 식에서 제거하는 방법을 사용하여 안정성을 얻을 수 있다

사용할 수 있는 라이브러리