1. 정보의 양

다음과 같은 상황을 생각해보자.

Attack or No Attack 두 가지만 표현할 수 있으면 된다. 즉, 0 or 1. 1비트면 가능하다.

만약, 동서남북 4개의 공격 방향을 추가로 더 알리고 싶다면 어떻게 될까?
동, 서, 남, 북의 4개의 정보를 알려주기 위해서는 2비트의 정보가 필요하다.
(00, 01, 10, 11로 표현가능하다.)
이걸 일반화 시키면 어떤 정보를 전달하는데 필요한 비트 수는 $-\log_2 p$ 로 계산된다. (두 개의 정보를 표현하는데 1비트가 필요하므로)

2. 정보 엔트로피

정보 엔트로피 $H(P)$는 정보전달에 필요한 평균 비트수이다.

$H(P) = \sum_{i} p_i(-\log_2 p_i)$

위의 예의 적용하면 Attack 과 No attack 으로만 나뉘었을 때는

$H = -(\frac12\log_2 \frac 12+\frac12\log_2 \frac 12) = 1$

1비트가 필요하고, 동서남북의 정보를 전달하기 위해서는

$H = -(\frac14\log_2 \frac 14+\frac14\log_2 \frac 14+\frac14\log_2 \frac 14+\frac14\log_2 \frac 14) = 2$

2비트의 정보가 필요하다는 것을 알 수 있다.

여기서, 재밌는 가정을 해보자. 만약 동, 서, 남, 북 각각 공격할 확률이 $\frac14$ 가 아니라 ($\frac{1}{10},\frac{2}{10},\frac{3}{10},\frac{4}{10}$)라면?

일단 위의 식 $H(P)$에 넣어서 계산부터 해보자.

$H = -(\frac{1}{10}\log_2 \frac {1}{10}+...+\frac{4}{10}\log_2 \frac {4}{10}) = 1.84644$

2비트보다 필요한 비트수가 줄어들었다.

즉, 완전히 랜덤한 상황보다 자주 발생하는 사건과 가끔 발생하는 사건이 구분될 때 정보 전달에 필요한 비트수가 줄어든다는 것을 알 수 있다.

간단하게 이야기해서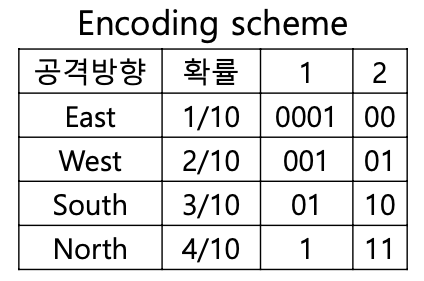
인코딩을 1번 방법과 같이 하는 경우 (자주 발생하는 사건에는 비트수를 줄이고 가끔 발생하는 사건에 비트수를 늘리면) 정보 전달에 필요한 평균 비트수가 줄어든다는 것을 직관적으로 알 수 있다.

짚고 넘어가야할 점은 위에서 도출한 1.84644의 값은 이론적으로 필요한 최소 비트수를 의미하는 것일 뿐, 최소비트수를 달성하기 위한 인코딩 방법이 무엇이냐는 별개다.

3. Cross entropy

만약, 실제 사건의 확률 분포가 오른쪽과 같았는데, 측정 결과가 없어서 왼쪽과 같은 분포를 가정하고 정보를 전송했다고 해보자.

그렇다면, 우리는 정보를 보낼 때 동, 서, 남, 북 모두 $-\log_2 q$인 2비트짜리 정보를 보냈지만, 실제 확률 분포는 ($\frac{1}{10},\frac{2}{10},\frac{3}{10},\frac{4}{10}$)이므로 평균적으로 정보전송에 든 평균 비트 수는

$-(\frac{1}{10}\log_2 \frac {1}{4}+\frac{2}{10}\log_2 \frac {1}{4}+\frac{3}{10}\log_2 \frac {1}{4}+\frac{4}{10}\log_2 \frac {1}{4}) = 2$

로 나타낼 수 있다.

이걸 Cross entropy로 정의한다. P의 확률을 따르고 있을 때 Q의 방법으로 정보를 전송한 것으로 $H(P||Q)$로 표현하며 식은 다음과 같다.

$H(P||Q) = \sum_{i} p_i(-\log_2 q_i)$

KL-divergence

이때 우리는 만약 P분포를 정확히 알았다면 아낄 수 있었던 평균 비트 수를 계산해 볼 수 있다.

P 분포를 정확히 알았을 때의 평균 비트 수는 위에서 구했었다.

$H(P) = -(\frac{1}{10}\log_2 \frac {1}{10}+...+\frac{4}{10}\log_2 \frac {4}{10}) = 1.84644$

둘의 차이가 아낄 수 있었던 평균 비트 수가 될 것이다.

$H(P||Q) - H(P) = 2-1.84644 = 0.15356$

이 때 H(P||Q) - H(P) 둘의 차이를 P와 Q의 분포의 차이, 거리라 해석할 수 있다. 이때 나온 개념이 KL-divergence이다. 식으로 정리하면 다음과 같다.

$D_{KL}(P||Q)=H(P||Q) - H(P) = -\sum_{i} p_i(\log_2 q_i-\log_2p_i)$

그렇다면 우리는 분류 문제를 풀 때, 이 $D_{KL}$ 값이 최소가 되도록 학습을 시킨다면 분류를 잘하는 모델이 될 것이라 생각할 수 있다.

하지만, 잘 생각해보면 우리가 파라미터의 값을 조절할 수 있는 것은 $q_i$일 뿐 $\log_2p_i$항이 아니다. 즉, 우리는 loss값으로 $D_{KL}$이 아닌 Cross entropy를 사용해도 된다.

4. Pytorch에서의 CrossEntropyLoss

pytorch에서는 CrossEntropyLoss를 기본으로 제공한다.

• 인풋에 소프트맥스를 자동으로 입혀주므로 인풋에는 확률 값이 아닌 logit 혹은 score 값을 넣어주어야한다.
• MNIST classifier를 예를 들어 설명하면 다음과 같다.

import torch

loss = torch.nn.CrossEntropyLoss()

score = torch.tensor([0.14, 0.9, 0.12, 0.21, 0.04,
0.06, 0.13, 0.4, 0.31, 0.21])
target = torch.tensor(1)

print(loss(score,target))

>>>
tensor(1.6879)

score는 model에 forward를 해준 후 나온 output이고, target은 이 때의 정답의 index가 1이라는 것을 의미한다.

즉, 정답의 확률 분포는 [0,1,0,0,0,0,0,0,0,0] 이므로 cross entropy는
$H(P||Q) = -0\times\log q_0-1\times\log q_1-0\times\log q_2-0\times\log q_3 - ... - 0\times\log q_9$

이 때의 $q_1$은 softmax 값이다. 다음과 같은 순서를 따라가면 직접 CrossEntropyLoss를 직접 계산할 수 있다.

1. output에 전부 torch.exp()를 씌운다.

torch.exp(score)

>>>
tensor([1.1503, 2.4596, 1.1275, 1.2337, 1.0408, 1.0618, 1.1388, 1.4918, 1.3634,
        1.2337])

2. torch.sum()으로 모두 더해준다.

torch.sum(torch.exp(score))

>>>
tensor(13.3015)

3. torch.exp()를 씌운 텐서의 인덱스가 1인 값 (2.4596)에 sum을 나눠준다.

torch.exp(score)[1]/torch.exp(score).sum()

>>>
tensor(0.1849)

4. 로그를 씌우고 마이너스를 곱한다.

print(-torch.log(torch.exp(score)[1]/torch.exp(score).sum()))
print(torch.nn.CrossEntropyLoss(score, target))
>>>
tensor(1.6879)
tensor(1.6879)

torch.nn.CrossEntropyLoss를 사용한 것과 동일한 값이 출력된다.