3. One Dimensional MC Integration

이현기·2022년 8월 23일

RayTracing:The-Rest-of-Your-Life

목록 보기

3/5

주의 사항

이 글은 RayTracing:The Rest of Your Life를 공부하며 작성한 글이다.

모든 사진, 글은 RayTracing:The Rest of Your Life에서 가지고 왔다.

영어 해석, 이론적으로 틀린 내용이 존재할 경우가 매우 크다. (지적해주시면 감사합니다.)

글을 쓰는 능력이 매우 안좋으니 이해해주세요. 연습 중 입니다.

이 Chapter는 pass 하시길 바랍니다.
아직 이해를 완전하게 못한 것 같아 잘못된 정보가 많습니다.

이제 1차원 안에서 MC Integration을 적용해 보자. Integration은 모든 area나 volumes들에 대해 계산을 진행한다. 때로는 Integration은 매우 복잡한 연산이 될 수도 있지만, 때로는 아주 깨끗하고 자연스러운 연산이 될 수도 있다.

Integration $x^2$

먼저 우리가 흔히 봤던 아래의 적분 공식을 보자.

I = \int^2_0 x^2dx

컴퓨터 과학에서는 아래와 같이 표시한다.

I = area(x^2, 0, 2)

처음보느..ㄴ...ㄷ...ㅔ...

위의 표시법을 또 다르게 표시할 수도 있다.

I = 2 \;\cdot\;average(x^2, 0, 2)

이것ㄷ...ㅗ...

#include "rtweekend.h"

#include <iostream>
#include <iomanip>
#include <math.h>
#include <stdlib.h>

int main() {
    int N = 1000000;
    auto sum = 0.0;
    for (int i = 0; i < N; i++) {
        auto x = random_double(0,2);
        sum += x*x;
    }
    std::cout << std::fixed << std::setprecision(12);
    std::cout << "I = " << 2 * sum/N << '\n';
    return 0;
}

위의 코드에서 우리는 수학적으로 얻는 값과 최대한 비슷한 값을 얻을 수 있게 된다.
위의 코드를 실행하면 2.66678983796.. 을 얻는 것을 확인했다. 이것은 또한 $\log(\sin(x))$ 와 같은 계산 또한 진행할 수 있다. 그래픽스 분야에서는 종종 우리가 evalute는 할 수 있지만 명시적으로 적을 수 없는 함수들이 존재한다. 우리가 여태 실습했던 코드에서 ray_color() 함수가 그렇다. 우리는 모든 방향에서 어떤 색이 보이는지 모르지만, 주어진 차원에서 통계적으로 추정할 수 있다.
우리가 맨처음에 실습했던 두 책의 문제점은 작은 light source가 너무 많은 noise를 만들어 낸다는 것이 문제다. 왜냐하면 이것은 충분히 균일한 샘플링이 이루어지지 않았기 때문에 생기는 것이라고 한다. 광원이 scatter될 때만 Light source를 샘플링 하기 때문이다. 그러나 이것은 약한 빛에 대해서는 불가능 할 수 도 있다. 또는 멀리있는 빛에 대해서도 마찬가지 이다. 그래서 이 약한 빛이나 멀리있는 빛에 대해 샘플을 더 보낸다면 우리는 이런 문제를 줄일 수 있다. 하지만 이런 방법은 정확하지 않은 밝기를 나타낼 수 있다. 따라서, 우리는 over-sampling을 조정하기 위해 downweighting을 함으로써 부정확한 샘플을 remove할 수 있다. 어떻게 oversampling을 조정할 수 있을까? 바로 probability density function(PDF) 라고 하는 방법을 사용하면 된다.

아직 잘 이해가 안되는 것 같다. 더 정확한 값을 얻기위해 sample의 개수를 늘린다는 것 같은데 거기에서 잘못된 sample을 지워서 더 정확한 값을 얻는다는 이야기인것 같다. 조정은 PDF를 이용.

Density Function

PDF 를 공부하기 앞서 먼저 Density Function은 무엇일까? Density Function이라는 것은 단지 연속적인 histogram form이다. 아래에 표시되는 사진은 histogram의 form을 보여주고 있다.

출처: 위키디피아

우리가 아마 데이터를 더 추가를 한다면 histogram이 나타내는 값은 점점 커질 것이다. 만약 우리가 데이터를 더 다양한 종류로 나눈다면 histogram들이 나타내는 값들이 점점 작아질 것이다.

즉, x축에 표현하는 값이 많아질수록 y값이 작아진다는 소리이다.

Discrete density function(이산 밀도 함수)는 y축을 백분율 또는 분수로 나타낸다는 점에서 histogram과 다르다. 연속적인 histogram은 (즉, x축이 무한대인 것) y축을 백분율 또는 분수로 나타낼 수가 없다. 그래서 Density Function은 x축의 Data를 추가할 때 마다, y값들이 0으로 되는 것을 막기위해 x축의 데이터를 가지고 온 다음, 그것을 조정하는 기능을 해준다. 위의 그래프에서 아래와 같이 적용할 수 있다.

bin\_height = \frac{Fraction \; of \; trees \; between \; height \; H \; and \; H'}{(H - H')}

위의 식을 이용해서 우리는 아래와 같이 추정할 수 있는 식을 얻을 수 있다고 한다.

Probability\;a\;random\;tree\;is\;between\;H\;and\;H' =\\ bin\_height \;\cdot\; (H - H^\prime)

우리는 그에 해당하는 확률을 알고싶다면 우리는 그 해당하는 면적을 더 하면 된다.

조금 더 보자...

Constructing a PDF

위에서 말하는 확률 밀도 함수인 PDF를 만들어 보고 사용해 보자. 먼저 $r$ 이라는 것이 자기 자신과 확률이 비례한 0과 2사이의 random한 값이라고 가정해보자. 그리고 그것에 대한 기댓 값을 PDF $p(r)$ 이라고 하자. 아래와 같이 그림으로 표시할 수 있다.

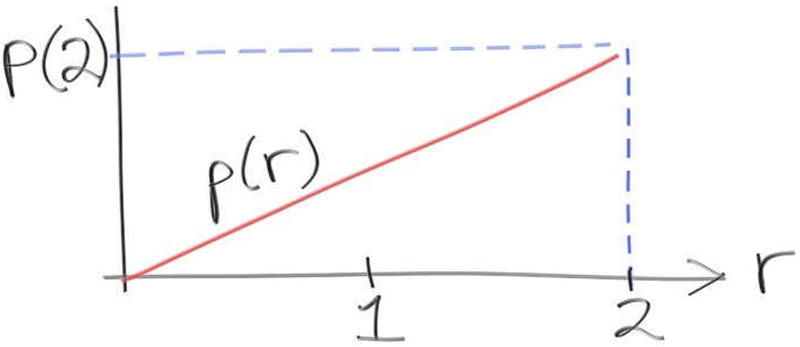
우리는 convention에 따라서 어떤 것이든 만들 수 있고 편리한 것을 선택해야 한다. 만약 r이라는 것을 발생할 확률을 구하고 싶다면 작은 범위를 이용해서 inegrate를 이용하여 구할 수 있다. 식은 아래와 같다.

영어해석이 많이 힘들지만 내가 이해한 바로는 Convention에 따라 우리가 원하는 확률을 구하고 싶다면 일정한 영역에 대한 적분을 진행하여 확률을 구할 수 있게 된다고 하는 것 같다.

Probability\; x_0 < r < x_1 = C \;\cdot\;area(p(r),x_0, x_1)

여기에서 $C$ 는 scale을 조정하는 상수를 뜻하는 것 같다. 만약 $C=1$ 이라면 조금 더 쉽게 계산을 진행할 수 있고 나온 결과 값이 바로 확률 값으로 얻을 수 있다. 그리고 위의 경우에서 우리는 r이 1을 어딘가에 가지고 있다는 것을 알 수 있다. 왜냐하면 영역의 넓이를 모두 더하게 된다면 1이라는 값을 얻을 수 있기 때문이다. 아래와 같이 작성해볼 수 있다.

area(P(r), 0, 2) = 1

area(C'r, 0, 2) = \int_{0}^{2} C' r dr = \frac{C'r^2}{2} \biggr|_{r=0}^{r=2} = \frac{C' \cdot 2^2}{2} - \frac{C' \cdot 0^2}{2} = 2C'

그래서 위의 두 식에서 우리는 $p(r) = r/2$ 라는 식을 얻을 수 있다. 그러면 이 PDF를 가지고 어떻게 random value를 생성할까?
우리는 여태 d = random_double() 함수를 이용해서 0과 1사이의 난수를 얻었다. 하지만 우리는 우리가 원하는 것을 주는 함수를 찾을 수 있어야 한다. $e = f(d) = d^2$ 이라는 것을 한번 가정해보자. 이거는 일정한 PDF가 아니다. $e$ 가 1미만에서는 0에 가까운 값을 가지고 1 초과일 경우에는 1보다 매우 큰 값을 가지게 되기 때문이다. 그래서 이 함수를 계산에 필요한 form으로 바꾸기 위해서는 cumulative probability distribution function (누적 분포 함수) $P(x)$ 가 필요하다.

P(x) = area(p, -\infty, x)

우리는 여기에서 우리가 x가 0일 때 값을 정의하지 않은 것을 주의해야 한다. 예시로 PDF $p(r) = r/2$ 을 표시한다면 :

P(x) = 0 : x < 0 \\ P(x) = \frac{x^2}{4}:0 < x < 2 \\ P(x) = 1: x > 2

여기에서 $r$ 은 인수의 역할을 한다. 그래서 예로 만약 $x = 1.0$ 이라면 우리는 아래와 같이 값을 얻을 수 있다.

P(1.0) = \frac{1}{4}

위의 값으로 이야기 할 수 있는 것은 PDF함수에서의 우리가 1미만의 값을 얻을 확률은 25%라는 것을 뜻한다. 이것은 일정하지 않은 난수를 생성할 때 기초가 된다. 우리는 f(random_double()) 라는 함수를 이용하여 PDF $\frac{x^2}{4}$ 을 이용한 return value를 얻을 수 있는 함수를 원한다. 우리는 이 return되는 값은 모르지만 그 값이 1.0보다 25%의 확률로 낮은 값일 수도 있고 그 값이 75%확률로 그 값이 1보다 클수도 있다는 것은 알 수 있다. 만약 f()가 증가한다면, 우리는 $f(0.25) = 1.0$ 라는 값을 기대할 수 있다. 이것을 일반화를 시키면 아래와 같다.

f(P(x)) = x

이걸 P에 관하여 다시 쓴다면 아래와 같다.

f(x) = P^{-1}(x)

이거는 inverse function이라고 하는 역함수를 뜻한다. 우리가 만약 PDF $p()$ 를 가지고 있고 누적 분포 함수 $P()$ 를 가지고 있다면 우리는 Inverse function을 구할 수 있다.

e = P^{-1}(random\_double())

우리의 PDF는 $p(x) = x/2$ 였다. 일치하는 누적 분포함수를 $P(x)$ 라 하자. 우리는 P의 Inverse를 구하기 위해서는 아래와 같은 과정을 해야한다.

y = \frac{x^2}{4}

x = \sqrt{4y}

그러면 아래와 같이 density p를 구해낼 수 있다.

e = \sqrt{4 \; \cdot \; random\_double()}

확률과 통계 책을 같이 보면서 다시 복습 필요!!!! 이 부분은 잘못된 부분이 많다 수정 필요!

Importance Sampling

우리는 integrand가 큰 곳에서 샘플링을 하고 있기 때문에 Noise가 적고 조금 더 빠르게 수렴할 수 있는 것을 기대할 수 있다. 사실은 우리가 샘플을 더 중요한 분포에 대해 조종하고 있는 것이다. 이것이 일정하지 않은 PDF를 사용하는 것이 importance sampling 이라고 불리는 이유이다.

그래서 우리는 정확한 답을 항상 반환하기 위해 다시 검토해 보자.
1. 너는 integral of $f(x)$ 를 [a, b]에 대해 가져야 한다.
2. 너는 0이 아닌 [a, b]에 대해서 PDF를 선택해야 한다.
3. You average a whole ton of $\frac{f(r)}{p(r)}$ where r is a random number with PDF $p$ .

항상 정답으로 수렴하지만 너가 PDF를 잘 선택하게 된다면 빠르게 수렴도 가능하다.

너무 어렵다... 이해가 잘 안되는 부분이 많아 복습이 많이 필요할 것 같다.

2022/08/26 추가글

글을 작성을 하고 조금 더 읽어보며 왜 이 MC Integration이 sampling에 필요한 이유와 그리고 이 책에서 설명한 것을 기준으로 곰곰히 생각을 해봤다. 앞 문단에서 우리는 이런 글을 확인 할 수 있다.

We can remove this inaccuracy by downweighting these samples to adjust for the over-sampling. How we do that adjustment? To do that, we will need the concept of a probability density function.

여기에서 설명하는 remove라는 단어를 주목하자. 우리는 위의 문장을 조금 쉽게 해석을 해서 이해한다면 아래와 같이 이해할 수 있다.

ray의 0과 1 사이의 값이라고 가정했을 때, 지금 들어온 ray의 값은 0.2이하일 확률이 80%이다. 그러면 낮은 에너지를 같는 ray일 수도 있겠네? quality에 영향이 있을 수도 있으니 없애는 것이 좋겠다! 또는 낮은 가중치를 두어 연산을 진행하자!

위의 글처럼 판단을 할 수 있을 수도 있다. 즉, 우리가 원하는 값에 대한 확률을 받기 때문에 이 값이 틀린 값일 수 있는 것을 판단을 하게 될 수 있는 것이다. 그래서 MC Integration을 하는 방법을 그 밑에 설명이 되는 것이다. 이로서 판단을 하게 된다음에 우리는 우리가 원하는 샘플들을 가지고 연산을 진행할 수 있게 된 것이다.

온전히 내 입장에서 내가 이해한 바로 작성했다. 이 chapter는 참고만 해주시면 감사하겠습니다.

이현기

안녕하세요!

이전 포스트

2. A Simple Monte Carlo Program

다음 포스트

3. One Dimensional MC Integration

RayTracing:The-Rest-of-Your-Life

Integration $x^2$

Density Function

Constructing a PDF

Importance Sampling

2022/08/26 추가글

2. A Simple Monte Carlo Program

4. MC Integration on the sphere of Directions

0개의 댓글

3. One Dimensional MC Integration

RayTracing:The-Rest-of-Your-Life

Integration x2x^2x2

Density Function

Constructing a PDF

Importance Sampling

2022/08/26 추가글

2. A Simple Monte Carlo Program

4. MC Integration on the sphere of Directions

0개의 댓글

Integration $x^2$