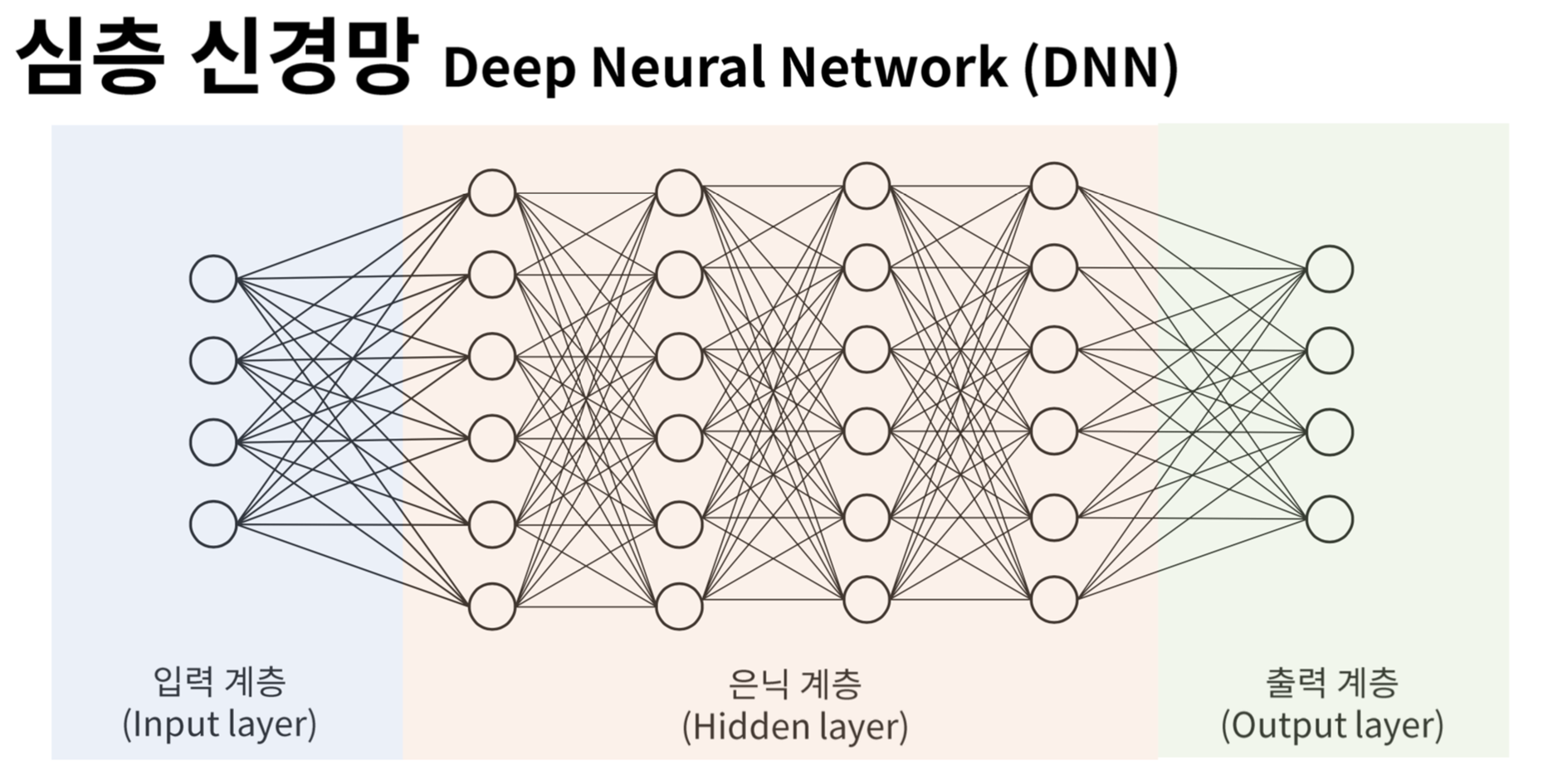
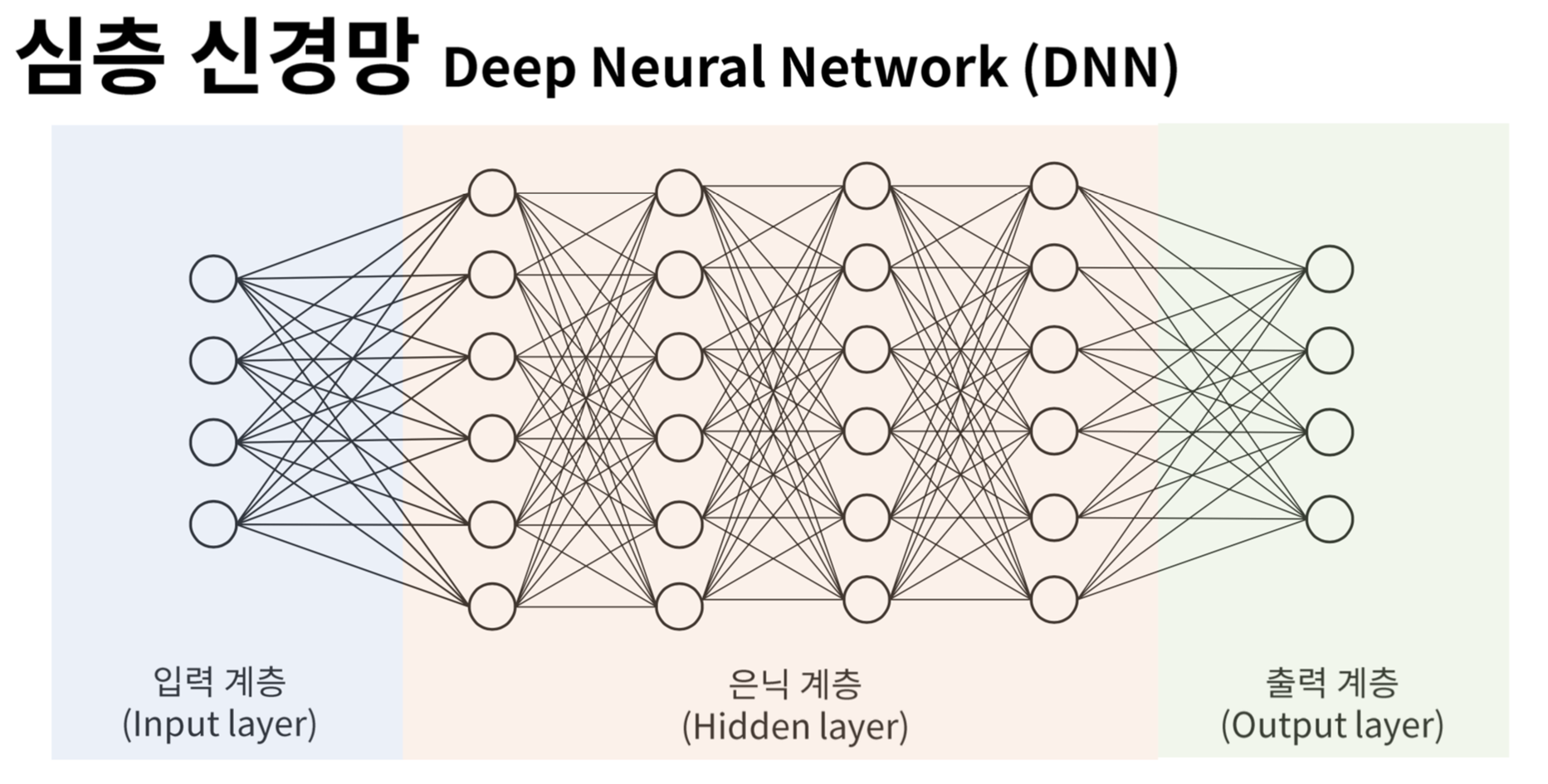
1. Deep Neural Network
1) 개념
Deep Neural Network(DNN, 심층 신경망)는 ANN의 확장 형태로, 여러 개의 Hidden Layer(은닉층)를 포함하는 인공 신경망을 의미한다. 여기서 은닉층이란 입력층과 출력층 사이의 모든 층을 말하는 것으로, 은닉층이 많아질수록 복잡한 패턴을 학습하기에 유리해진다.
은닉층의 목적은 비선형 연산을 수행하는 데에 있다. 만약 은닉층에서도 선형 연산만 수행한다면 어떻게 될까? 예를 들어, 하나의 은닉층으로 구성된 DNN에서 아래와 같은 연산을 수행한다고 해보자.
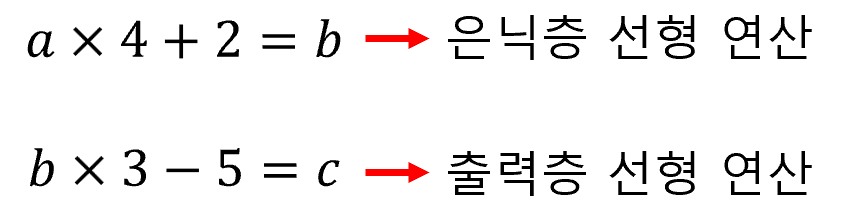
위에 나타난 두 개의 선형 방정식은 사실, a x 12 + 1 = c라는 하나의 선형 방정식으로 나타낼 수 있다. 즉, 은닉층 없이도 동일한 결과를 얻을 수 있다는 것이다. 그러므로, 은닉층에서는 출력층에서 계산할 수 없는 비선형 연산을 수행해야 한다.

은닉층에는 반드시 활성화 함수가 포함되어 있다. 은닉층에서 사용할 수 있는 활성화 함수는 출력층 활성 함수에 비해 매우 다양한데, 여기서는 Sigmoid와 ReLU 함수에 대해서만 알아보기로 하겠다.
2) DNN 모델 만들기
① Fashion MNIST 데이터 Set을 불러온다.
from tensorflow import keras
(train_input, train_target), (test_input, test_traget) = keras.datasets.fashion_mnist.load_data()② 픽셀 값을 정규화하고, 특성 데이터를 1차원으로 변환한다.
train_scaled = train_input / 255
train_scaled = train_scaled.reshape(-1, 28 * 28)③ 검증 Set을 떼어낸다.
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target, test_size=0.2, random_state=42)④ keras.layers 패키지의 Dense 클래스를 사용하여 두 개의 밀집층을 만들어보자.
- 은닉층에서는 Sigmoid 함수를, 출력층에서는 Softmax 함수를 사용한다.
- 은닉층의 뉴런 개수를 정하는 명확한 기준은 없지만, 적어도 출력층 뉴런보다는 많아야 한다. 여기서는 100개의 뉴런을 사용하도록 하겠다.
- 첫번째 층에서 input_shape을 지정한 이후에는, 이전 층의 출력이 자동으로 다음 층의 입력이 된다. 따라서, 두번째 층부터는 input_shape을 지정할 필요가 없다.
dense1 = keras.layers.Dense(100, activation='sigmoid', input_shape=(784,))
dense2 = keras.layers.Dense(10, activation='softmax')⑤ Keras의 Sequential 클래스를 사용하여, 위에서 만든 밀집층을 갖는 DNN 모델을 생성한다.
- 밀집층이 여러 개일 경우, 입력 인자로 리스트를 사용한다.
- 반드시 밀집층의 순서대로 리스트에 적재되어야 한다.
- 여러 개의 층을 사용하면 복잡한 비선형 연산이 가능해지므로, 모델이 더욱 강력한 성능을 발휘하게 된다.
model = keras.Sequential([dense1, dense2])⑥ summary() 메서드를 사용하면, 각 층에 대한 정보를 얻을 수 있다.
model.summary()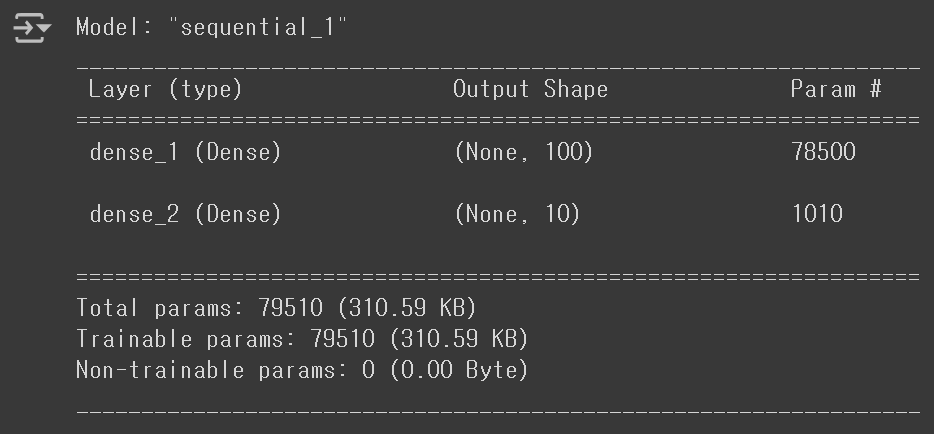
- Model: 모델의 이름
- Layer: 층 이름
- Output Shape
- None: Keras 모델은 Mini-batch 경사 하강법으로 훈련되기 때문에, 다양한 배치 크기에 유동적으로 대응할 수 있도록 Batch 크기를 명시하지 않는데, 이러한 의미에서 Batch Size를 None으로 지정한다.
- 100: 해당 밀집층에 존재하는 뉴런의 개수
- Param: 해당 밀집층에 존재하는 가중치와 절편의 개수로,
784 X 100 + 100 = 78500으로 계산되었다.- Trainable params: 모델 학습 과정에서 업데이트되는 파라미터
- Non-trainable params: 업데이트되지 않는 고정 파라미터
⑦ 층을 추가하기 위해 add() 메서드를 사용할 수도 있다.
- 모델의 이름과 층 이름은 반드시 영어로 지정해야 한다.
- 띄어쓰기도 사용할 수 없다.
model = keras.Sequential(name='Fashion_MNIST_DNN')
model.add(keras.layers.Dense(100, activation='sigmoid', input_shape=(784,), name='hidden'))
model.add(keras.layers.Dense(10, activation='softmax', name='output'))
model.summary()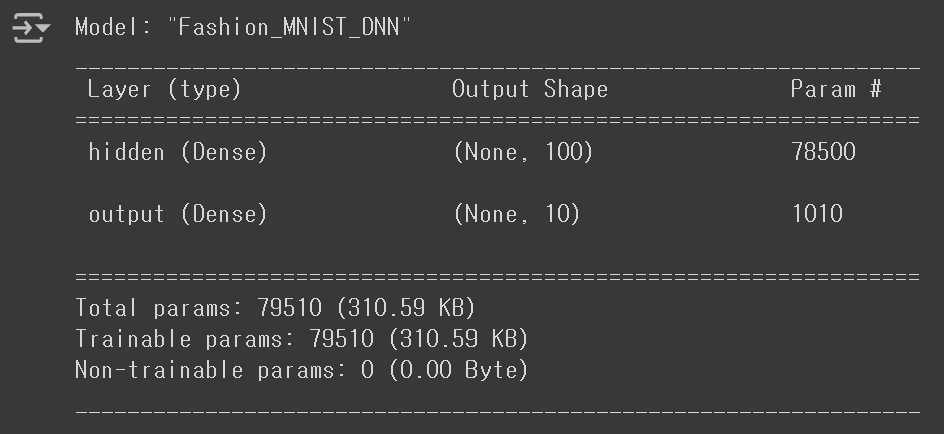
⑧ compile() 메서드를 사용하여 사전 설정을 진행한 후, 모델을 훈련시켜보자.
- 추가된 층으로 인해, 모델의 성능이 향상되었다.
model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
model.fit(train_scaled, train_target, epochs=5)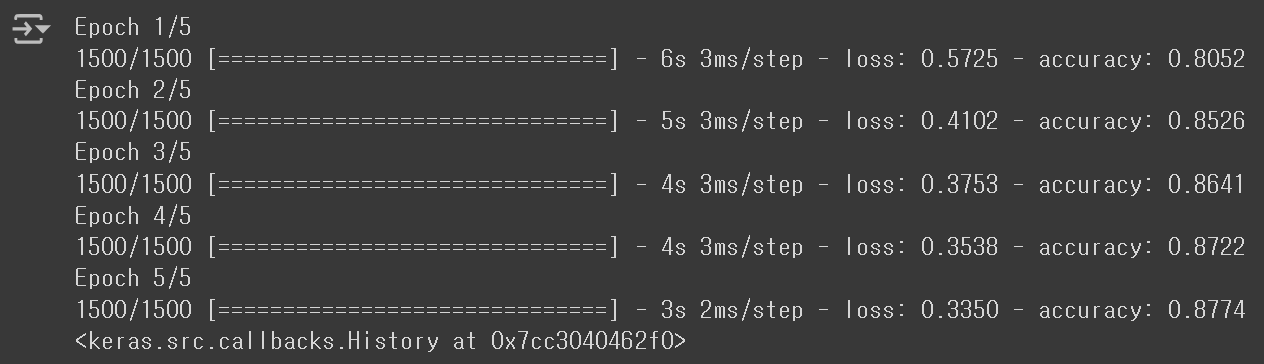
2. ReLU Function
1) Sigmoid Function의 한계
초기 인공 신경망의 은닉층에는 주로 Sigmoid 함수가 사용되었다. 하지만, Sigmoid 함수에는 아래와 같은 치명적인 문제점이 존재했다.
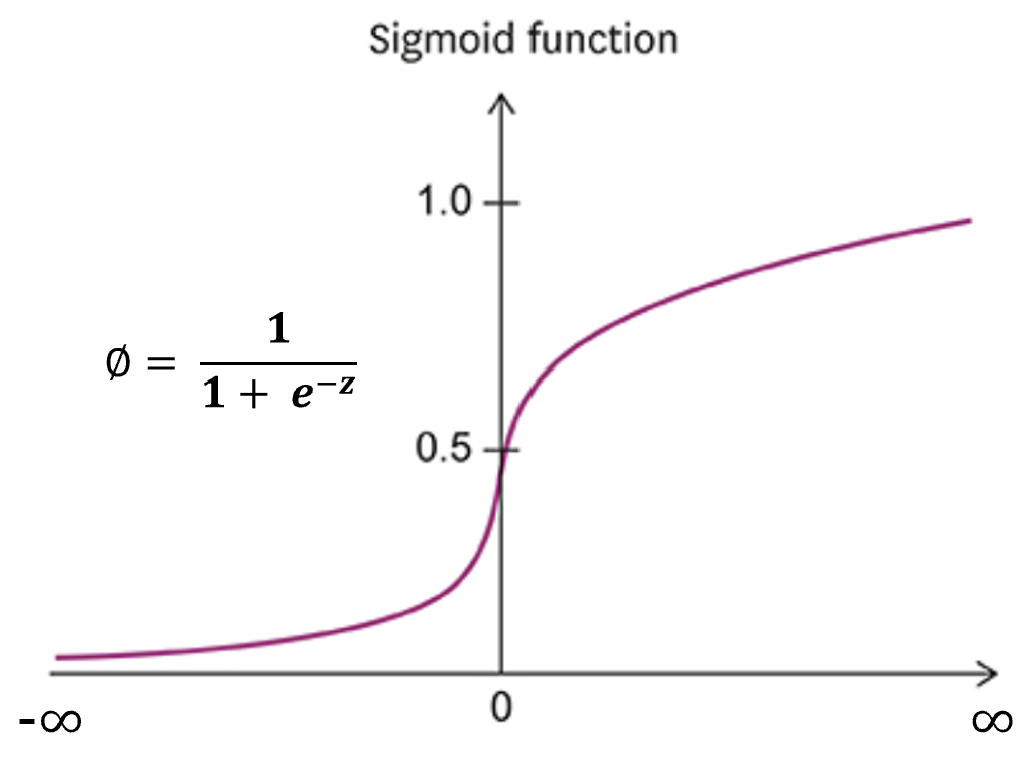
① Vanishing Gradient(기울기 소실) Problem
- 심층 신경망의 학습은 주로 Backpropagation(역전파) 알고리즘을 통해 이루어진다.
- Backpropagation은 손실 함수의 기울기를 계산하여, 가중치 업데이트를 수행하는 알고리즘이다.
- 그러나 Sigmoid Function의 경우, 입력 값이 매우 크거나 작을 때 기울기가 0에 수렴하기 때문에, 가중치 업데이트가 거의 이루어지지 않게 된다.
② Non Linearity(비선형성) Problem
- 지수 함수를 포함하기 때문에, 일반 선형식에 비해 계산 비용이 크다.
- 입력 값의 변화와 출력 값의 변화가 비례하지 않는다.
③ Non-Zero Centered(비중심화) Problem
- Sigmoid 함수의 출력 값은 0과 1 사이에 위치하기 때문에, 출력의 평균값이 0이 아니다.
- 이는 역전파의 효율을 낮추기 때문에, 수렴 속도를 저하시킨다.
2) ReLU Function
이러한 문제점을 개선하기 위해 제안된 함수가 바로 ReLU Function이다. ReLU 함수는 양수 입력은 통과시키고, 음수 입력은 0으로 만드는 함수로, 아래와 같은 형태를 갖는다.
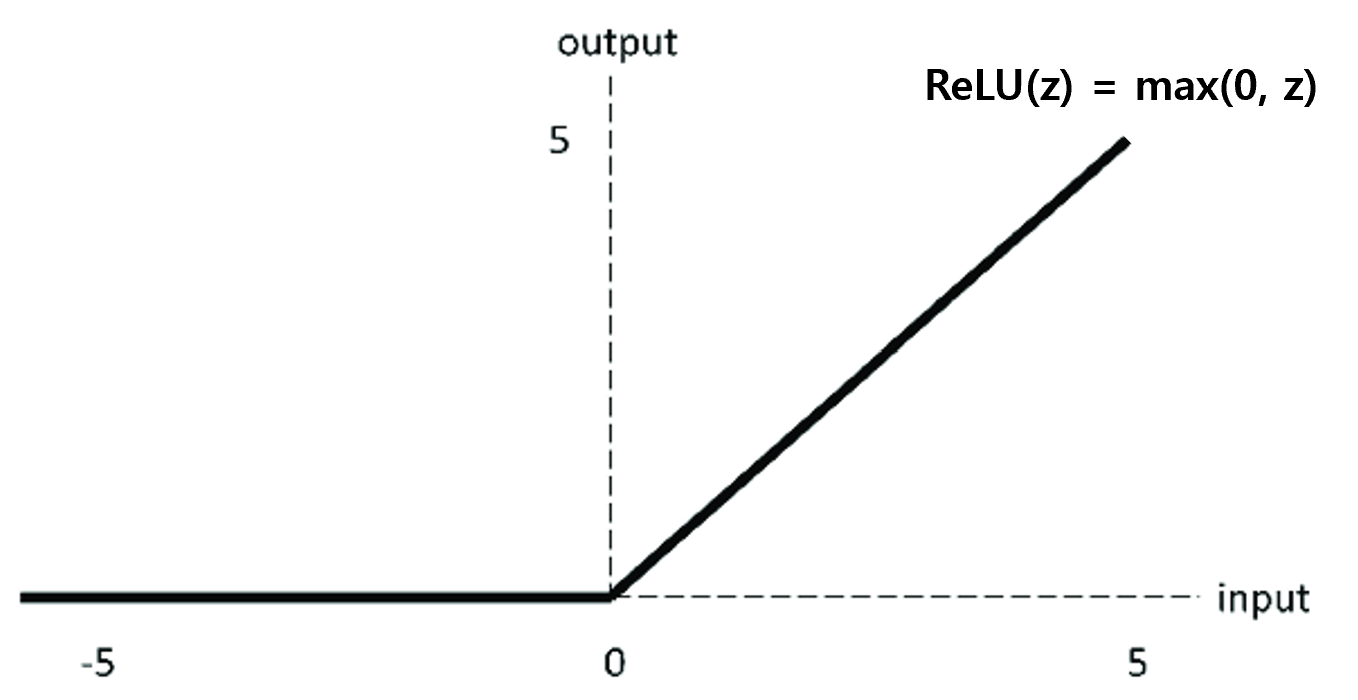
ReLU 함수를 사용하면, 위에서 설명한 Sigmoid 함수의 기울기 소실과 비선형성 문제를 해결할 수 있다. 물론, Non-Zero Centered 문제가 여전히 발생하고 있으며, 음수 입력에 대한 처리가 불가능하다는 것은 단점이다. 하지만, 수렴 속도가 매우 빠르기 때문에, 양수 입력만 사용하는 이미지 처리 등의 문제에서 매우 높은 성능을 자랑한다.
3. Flatten Layer
지금까지는 2차원의 특성(픽셀) 데이터를 사용하기 위해, reshape() 메서드를 이용해 특성 데이터를 1차원으로 변환해주었다. 그러나 사실 이러한 방법보다는, 입력층과 은닉층 사이에 Flatten Layer를 추가하는 방식이 더욱 권장된다.
model = keras.Sequential()
model.add(keras.layers.Flatten(input_shape=(28, 28)))
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))참고로, Flatten Layer는 학습에 사용되는 층이 아니므로, 신경망의 깊이는 여전히 2로 취급된다. 위와 같은 방식이 더욱 권장되는 이유는 입력 값의 차원(개수)이 summary() 메서드의 결과에 함께 출력되기 때문이다.
model.summary()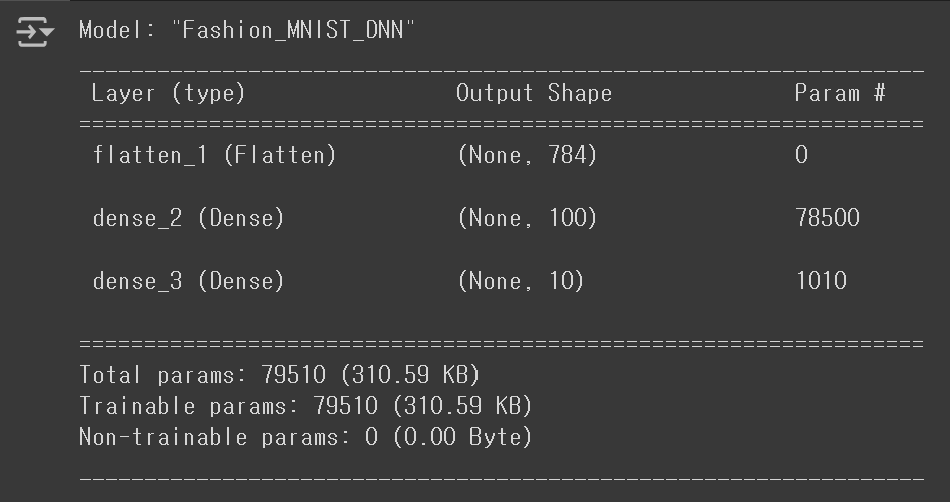
Flatten Layer을 사용함으로써, 입력 값의 차원이 784라는 사실을 쉽게 알 수 있게 되었다. 이제 Flatten Layer을 활용하여 모델을 훈련시키고, 성능을 확인해보자.
(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()
train_scaled = train_input / 255
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target, test_size=0.2, random_state=42)
model = keras.Sequential(name='Fashion_MNIST_DNN')
model.add(keras.layers.Flatten(input_shape=(28, 28)))
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))
model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
model.fit(train_scaled, train_target, epochs=5)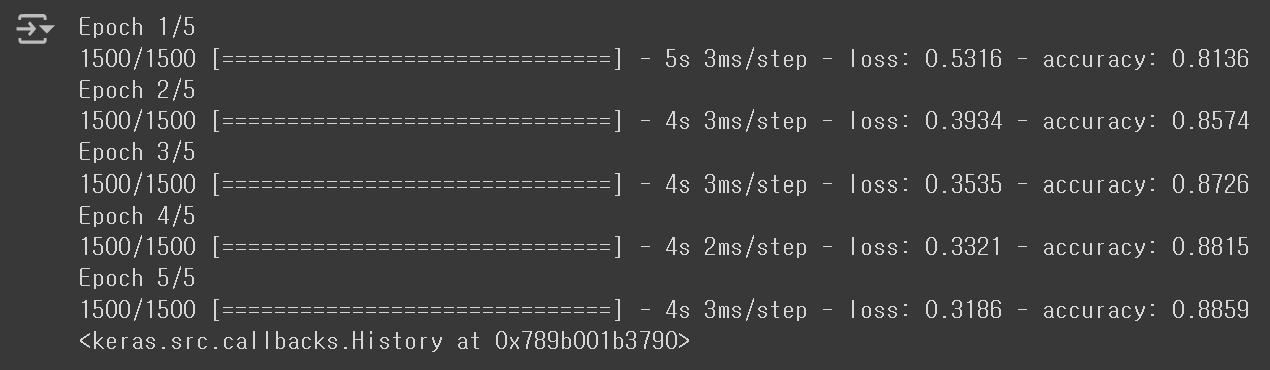
Sigmoid 함수를 사용했을 때보다, 성능이 조금 더 향상된 것을 확인할 수 있다. 계속해서 검증 Set에서의 성능도 평가해보자.
model.evaluate(val_scaled, val_target)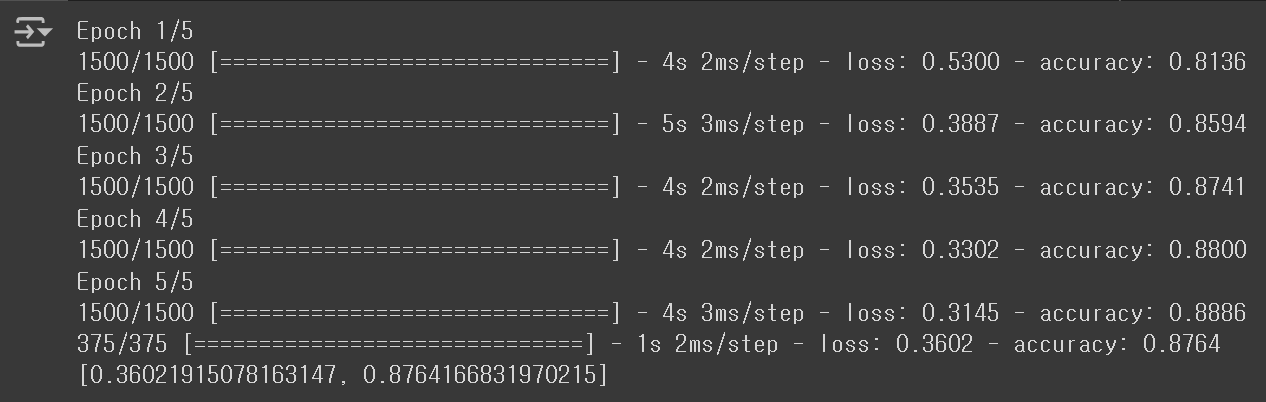
지난 ANN 모델의 점수가 0.8475였던 것과 비교하면, 유의미한 성능 향상이라고 판단할 수 있을 것 같다.
4. Optimizer
Keras에서는 손실 함수를 최소화하기 위해 모델의 가중치를 조정하는 다양한 알고리즘을 제공하는데, 이를 Optimizer라고 부른다. 참고로, compile() 메서드에서는 Keras의 기본 경사 하강법인 RMSprop을 사용한다.
각 Optimizer에는 지정해주어야 하는 하이퍼파라미터가 존재하는데, 대표적인 예시 몇 가지를 살펴보면 아래와 같다.
1) SGD
이름은 SGD이지만, 기본적으로 Mini-batch 경사 하강법을 사용한다. 사용되는 하이퍼파라미터는 아래와 같다.
① learning_rate(학습률)
- 경사 하강에 사용할 스텝의 크기를 의미한다.
- 너무 크면 최적점을 지나칠 수 있고, 너무 작으면 학습 속도가 느려질 수 있다.
② momentum
- 이전 기울기 값을 반영할 비율로, 수렴 속도를 가속하는 효과가 있다.
- 주로, 0.9 이상의 값으로 지정한다.
- momentum의 값을 0 이상으로 지정하는 것을, Momentum Optimization이라 한다.
③ nesterov(네스테로프 모멘텀)
- Momentum 기법을 개선하여 더 빠른 수렴을 유도한다.
- True/False를 통해 지정된다.
- nesterov를 True로 지정하는 것을, Nesterov Momentum Optimization이라 한다.
sgd = keras.optimizers.SGD(learning_rate=0.1, momentum=0.9, nesterov=True)
model.compile(optimizer=sgd, loss='sparse_categorical_crossentropy', metrics='accuracy')일반적으로 Nesterov Momentum Optimization이 기본 SGD보다 높은 성능을 제공한다.
2) Adagrad/RMSprop
모델이 최적점에 가까워질수록 학습률을 낮춘다면, 수렴 속도를 개선하면서도 최적점에 수렴할 가능성을 높일 수 있을 것이다. 이러한 학습률을 Adaptive Learning Rate(적응적 학습률)라고 한다. 적응적 학습률이 적용된 대표적인 Optimizer에는 Adagrad와 RMSprop이 있다. 주로 사용되는 하이퍼파라미터는 learning_rate로 초기에 사용될 기본 학습률을 의미한다.
adagrad = keras.optimizers.Adagrad(learning_rate=0.01)
model.compile(optimizer=adagrad, loss='sparse_categorical_crossentropy', metrics='accuracy')
rmsprop = keras.optimizers.RMSprop(learning_rate=0.01)
model.compile(optimizer=rmsprop, loss='sparse_categorical_crossentropy', metrics='accuracy')3) Adam
Adam은 Momentum Optimization과 RMSprop의 장점을 결합한 Optimizer이다. Adam에서 주로 사용되는 하이퍼파라미터도 역시 learning_rate인데, 여기서는 기본 Adam Optimizer를 활용하여 모델을 훈련시켜보도록 하겠다.
참고로, SGD, RMSprop, Adam을 기본 Optimizer로 사용할 때에는, optimizer='sgd'와 같이 문자열만 전달하면 된다.
model = keras.Sequential()
model.add(keras.layers.Flatten(input_shape=(28, 28)))
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics='accuracy')
model.fit(train_scaled, train_target, epochs=5)
model.evaluate(val_scaled, val_target)
